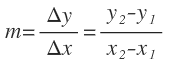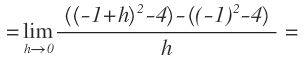En esta lección voy a explicarte la interpretación geométrica de la derivada, es decir, qué es una derivada desde el punto de vista gráfico.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Tienes disponibles el Curso de Derivadas donde te explico con todo detalle cómo derivar todo tipo de funciones.
A continuación, te demostraré qué es la derivada geométricamente y resolveremos un ejercicio aplicando lo aprendido.
¡Vamos allá!
Demostración de la interpretación geométrica de la derivada
Este es el concepto más importante que te tienes que aprender de esta lección:
Vamos a demostrar por qué esto es así.
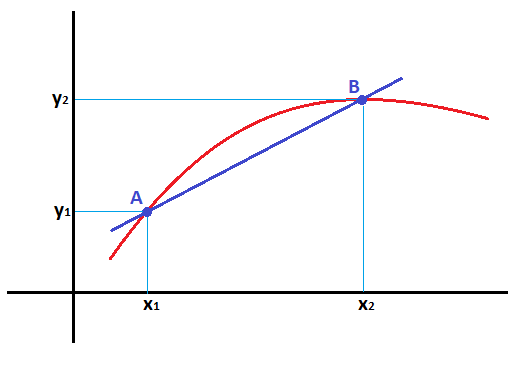
Supongamos que tenemos una función, a la que cortamos con una recta secante en dos puntos A y B, cuyas coordenadas son:
Representándolo quedaría de la siguiente manera:
Por cierto, se le llama recta secante porque corta a la función en dos puntos. La pendiente de esa recta secante (y de cualquier recta) se calcula como el cociente entre el incremento entre valores de «y» entre el incremento de valores de x:
Por otro lado, se puede formar un triángulo rectángulo con la recta secante entre los puntos A y B, trazando una línea horizontal desde A y una línea vertical desde B, donde vemos que la recta secante forma un ángulo α con la horizontal:
La tangente de un ángulo se calcula con la siguiente fórmula:
En nuestro caso, el cateto opuesto al ángulo es la diferencia entre las coordenadas «y» y el cateto adyacente al ángulo es la diferencia entre las coordenadas x, por lo que la tangente de α la podemos expresar como:
Es decir, el mismo valor que la pendiente de la recta secante.
Por tanto, la pendiente de la recta secante es igual a la tangente del ángulo que forma la recta con la horizontal:
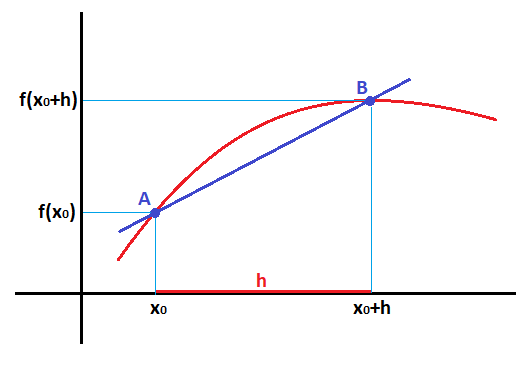
Ahora, a la coordenada x del punto A, la llamaremos X0 y para controlar cuánto aumenta la coordenada B cuando nos movemos hacia el punto B, a ese aumento le llamaremos «h» y por tanto la coordenada x del punto B será X0+h. Lo nombramos así para controlar el aumento de la coordenada x de B con respecto a la de A.
La coordenada «y» del punto A, corresponde al valor de la función cuando X=X0 es decir f(X0) y por tanto, siguiendo la misma lógica, la coordenada «y» del punto B sería f(X0+h)
Si te das cuenta, las coordenadas de los puntos A y B siguen siendo las mismas, tan sólo les he cambiado el nombre. Las nuevas coordenadas de los puntos A y B serían:
Igual que antes, podemos formar un triángulo rectángulo con la recta secante, donde ahora el cateto opuesto al ángulo toma el valor de f(X0+h)-f(X0) y el cateto adyacente al ángulo toma el valor de «h», que era el aumento de la coordenada x de B, con respecto a la de A:
Con esta nomenclatura, la pendiente de la recta secante la expresamos como:
Que coincide con la expresión de la tasa de variación media.
La tangente del ángulo α se expresa como:
Hasta aquí tan solo te he explicado como se puede expresar la pendiente de una recta, que la expresamos en función de las coordenadas x de dos puntos, teniendo en cuenta la diferencia entre ellas (h).
Vamos a ver qué pasa cuando el punto B se aproxima al punto A siguiendo la función:
Conforme el punto B se aproxima al punto A, la diferencia entre sus coordenadas x, h, se va haciendo cada vez más pequeña.
Si B se aproximara tanto a A, que se confundiera con el punto A, o dicho de otra forma, cuando h tiende a 0, la recta secante se convierte en una recta tangente, que solamente corta a la función en el punto A:
En ese caso, la pendiente de la recta tangente en el punto A, sería le límite de cuando h tiende a cero de la fórmula de la pendiente:
Que coincide con la fórmula de la derivada de una función en un punto:
Por tanto, la pendiente de la recta tangente a una función en un punto es igual a la derivada de la función en ese punto, que también coincide con la tangente del ángulo que forma la recta tangente con la horizontal:
Ejercicio resuelto de cálculo de la recta tangente en un punto
Vamos a resolver un ejercicio aplicando todo lo que acabamos de ver.
Los ejercicios habituales para aplicar la interpretación geométrica de la derivada es calcular la recta tangente a una determinada función en un punto.
La ecuación de una recta tiene esta forma:
Por tanto, nos obliga a obtener la pendiente m, y es ahí donde la calculamos con la derivada de la función en ese punto, según su definición, tal y como acabamos de ver:
La ecuación de la recta la obtendremos mediante la ecuación punto-pendiente:
Por lo que también necesitaremos las coordenadas del punto donde la recta es tangente a la función:
Se mezclan, por tanto, conceptos de geometría y de calculo de derivadas
Vamos a ver un ejemplo para que quede todo mucho más claro:
Hallar la ecuación de la recta tangente a la curva:
en el punto de abcisa x=-1.
Tal y como te acabo de indicar, la ecuación de la recta la calcularemos con la ecuación punto-pendiente:
Por tanto, necesitamos saber las coordenadas de un punto, que sea tangente a la curva y que pase por la recta:
Y la pendiente de la recta, que coincide con la derivada en ese punto:
Empezamos calculando las coordenadas del punto P.
Ya sabemos la coordenada x, ya que nos la da el enunciado. Para calcular la coordenada «y», sólo tenemos que calcular el valor de al función en el punto x=-1, sustituyendo la x por -1:
Por lo tanto, las coordenadas del punto P, donde la recta es tangente son:
Ahora vamos a calcular la pendiente, que es igual a la derivada en x=-1:
Calculamos la derivada en x=-1 usando la definición de derivada:
Sustituimos (-1+h) y (-1) en sus funciones correspondientes:
Operamos en el numerador:
Sacamos factor común a la h para poder eliminarla en el numerador y en el denominador:
Y finalmente resolvemos el límite:
La pendiente por tanto es igual a -2:
Sustituimos el valor de la pendiente y las coordenadas del punto en la ecuación punto-pendiente:
Operamos para eliminar paréntesis:
Y despejamos la «y», llegando finalmente a la ecuación de la recta tangente que nos están pidiendo:
Ejercicios propuestos
1- Dada la siguiente función:
Calcula la ecuación de la recta tangente a la función en el punto x=1
2 – Calcula la ecuación de la recta tangente a la parábola:
en los puntos donde la parábola corta al eje x de coordenadas.
¿Quieres aprender a derivar desde cero? Pues te recomiendo el Curso de Derivadas, en el que te enseñaré paso a paso a derivar todo tipo de funciones, con ejercicios resueltos paso a paso y ejercicios propuestos para que practiques. Además me puedes preguntar todas tus dudas.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: