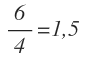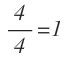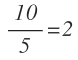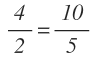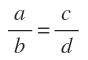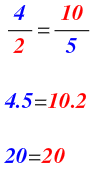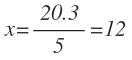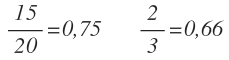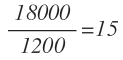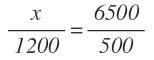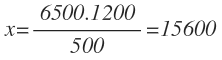En esta lección te voy a explicar qué es la razón entre dos números y qué es una proporción. Lo veremos con ejemplos y ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué és la razón entre dos números
La razón entre dos números es el resultado de dividir dichos números.
Por ejemplo, la razón entre 4 y 2 es 2, ya que es el resultado realizar el cociente de esos números:
La razón no se mide en ninguna unidad.
Al dividir dos números entre sí, lo que estamos haciendo es comparar el primer número con el segundo número, por tanto, la razón nos sirve para indicar cuántas veces el primer número es el segundo número, o lo que es lo mismo, por qué número hay que multiplicar el segundo número para obtener el primero.
En el ejemplo anterior, cuando calculamos la razón entre 4 y 2, estamos comparando 4 con 2 y que la razón sea 2 nos indica que 4 es 2 veces 2, es decir, es el doble.
Como te acabo de comentar, con la razón entre dos números comparamos el primer número entre el segundo número. Así que, ten en cuenta que el primer número no tiene por qué ser siempre el mayor de los dos.
También podemos calcular la razón entre 2 y 4, que es 0,5:
Sólo tienes que tener en cuenta que a la hora de definir la razón entre esos dos números, tienes que nombrar primero al número que colocas en el numerador, ya que comparas el número que está en el numerador con el que está en el denominador.
Que la razón entre 2 y 4 sea igual a 0,5, nos está indicando que 2 es 0,5 veces 4. En este caso, 0,5 es igual a la mitad, por lo que 2 es la mitad que 4.
Si te das cuenta, que 4 sea el doble de 2 o que 2 sea la mitad que 4, realmente es lo mismo, ya que estamos comparando los mismo números.
Cuando el primer número es mayor que el segundo, su razón es mayor que 1. Por ejemplo la razón entre 6 y 4 es 1,5:
Lo que indica que 6 es 1,5 veces 4.
Cuando el primer número es menor que el segundo, su razón es menor que 1. Por ejemplo, la razón entre 2 y 3 es 0,66:
Lo que indica que 2 es 0,66 veces 3
Si los dos números son iguales, la razón es igual a 1:
Ejercicios resueltos de razón entre dos números
Vamos a resolver unos ejercicios aplicando lo que te acabo de explicar.
Ejercicio 1
Un saco grande de arena pesa 5,8 kg y un saco pequeño pesa 2,3 kg. ¿Cuál es la razón entre el peso del saco grande y el peso del saco pequeño? ¿Qué indica esa razón?
Nos preguntan la razón entre el saco grande y el saco pequeño, luego nos están preguntando la razón entre 5,8 y 2,3, que es, por lo que el primer número es 5,8, que es el que va en el numerador y 2,3 es el segundo número que va en el denominador:
Esa razón nos indica que el peso del saco grande es 2,52 veces el peso del saco pequeño.
En este problema, date cuenta de que la razón no es una fracción, ya que en una fracción el numerador y el denominador deben ser números enteros y en una razón pueden ser números decimales.
Ejercicio 2
En una frutería hay 25 manzanas y 35 naranjas. ¿Cuál es la razón entre manzanas y naranjas? ¿Y entre naranjas y manzanas? ¿Qué nos indica cada razón?
La razón entre manzanas y naranjas es:
Lo que indica que el número de manzanas es 0,71 veces el número de naranjas.
Por otro lado, la razón entre naranjas y manzanas es:
Lo que indica que el número de naranjas es 1,4 veces el número de manzanas.
Decir que el número de manzanas es 0,71 veces el número de naranjas y que el número de naranjas es 1,4 veces el número de manzanas es lo mismo.
Proporción
La proporción es una igualdad entre dos razones, que evidentemente, son iguales.
Por ejemplo:
La razón entre 4 y 2 es:
Y la razón entre 10 y 5 es:
La igualdad de esas dos razones forman una proporción:
Una proporción es una igualdad donde cada uno de los miembros es una razón.
En general, una proporción:
Se lee como: «a» es a «b» como «c» es a «d».
De esta forma, la proporción del ejemplo anterior se lee como 4 es a 2 como 10 es a 5.
En una proporción se cumple que el producto del numerador de la razón del primer miembro por el denominador de la razón del segundo miembro, es igual al producto del denominador de la razón del primer miembro por el numerador de la razón del segundo miembro.
En la proporción del ejemplo anterior:
Es decir, al multiplicar en cruz y operar, el resultado es el mismo.
Esto nos permite calcular el valor de uno de los números de las razones, conocidos el resto de valores, para que sea una proporción.
Por ejemplo, ¿cuál debe ser el valor de la x para que ambas razones formen una proporción?
Multiplicamos en cruz y nos queda:
Ahora despejamos la x pasando el 5 dividiendo al segundo miembro y operamos:
Por tanto, x debe ser igual a 12 para que esa igualdad de dos razones sea una proporción.
Ejercicios resueltos sobre proporciones
Ejercicio 1
¿Las siguientes razones forman una proporción?
Para que formen una proporción, ambas razones deben ser iguales.
Si calculamos por separado cada razón nos da:
Por tanto, no forman una proporción.
Además, tampoco se verifica que al multiplicar en cruz y operar el resultado sea el mismo:
Ejercicio 2
En la carretera A pasaron en el mes de diciembre 1200 vehículos y al año han pasado un total de 18000 vehículos. En la carretera B pasaron el mismo mes de diciembre 500 vehículos y al año, han pasado un total de 6500 vehículos.
a) Calcula las razones entre el número vehículos al año y el número de vehículos en el mes de diciembre para cada carretera e indica si forman una proporción.
b) ¿Cuántos vehículos deberían haber pasado al año por la carretera A para que las razones de ambas carreteras formen una proporción?
Apartado a:
La razón entre el número vehículos al año y el número de vehículos en el mes de diciembre para la carretera A es:
La misma razón para la carretera B es:
No forman una proporción ya que las razones no son iguales.
Apartado b:
Vamos a calcular la cantidad de vehículos que deberían haber pasado al año por la carretera A, para que ambas razones formen una proporción.
Para ello, igualamos ambas razones para que formen una proporción y al dato de los vehículos al año de la carretera A le llamamos x:
Ahora multiplicamos en cruz:
Despejamos la x y operamos:
Para que ambas razones formen una proporción, deberían haber pasado 15600 vehículos al año por la carretera A.
Si quieres seguir aprendiendo cómo hacer reglas de tres directas e inversas, reglas de tres compuestas o aumentos y disminuciones porcentuales, te recomiendo el Curso de Proporcionalidad, con ejercicios resueltos paso a paso.
Ejercicios propuestos
1- Un equipo de baloncesto ha anotado 87 puntos y ha encajado 65 puntos ¿Cuál es la razón entre puntos anotados y puntos encajados? ¿Y entre puntos encajados y puntos anotados? ¿Qué indica cada razón?
2- La razón de dos números es 3, si el menor es 5 ¿Cuál es el número mayor?
3- Si 10 es a x lo mismo que 8 es a 4, ¿cuál es el valor de x?
4- En una clase hay 15 niños y 12 niñas. En el colegio, hay en total 375 niños y 250 niñas. Calcula la razón entre los niños y niñas de la clase y del colegio. Indica si forman una proporción y en caso que no la formen, calcula cuantas niñas tendría que haber en la clase para que la formen.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: