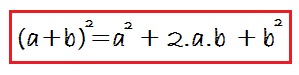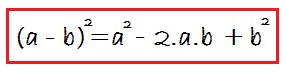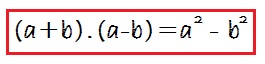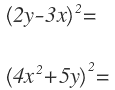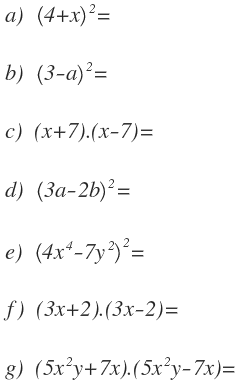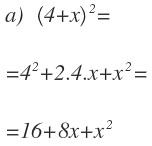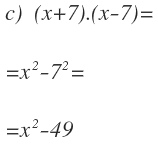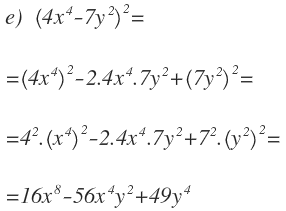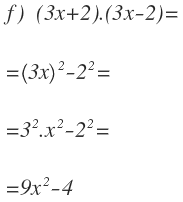Qui vi spiegherò quali sono i prodotti notevoli, noti anche come identità notevoli. Vedremo le formule di ciascuno di essi e li applicheremo per mezzo di esercizi risolti passo dopo passo.
Sto andando a spiegare passo dopo passo le diverse formule dei prodotti notevoli, con esempi risolti passo dopo passo, in modo che si impara ad applicarli.
Cosa sono i prodotti o le identità notevoli
Che cosa sono i prodotti notevoli?
Prodotti notevoli, chiamati anche identità notevoli, sono polinomiali di due termini (binomiali) al quadrato, o il prodotto di due binomiali, come vedremo più avanti, il cui sviluppo segue sempre le stesse regole.
Moltiplicando due polinomi con l’altro, se hanno più di tre termini, può essere molto noioso e si può spendere un sacco di tempo a fare la moltiplicazione. Le formule dei prodotti notevoli, che vi permetterà di effettuare la moltiplicazione direttamente, senza dover andare termine per termine.
Binomiale al quadrato
Per la cronaca, vediamo cos’è un binomio quadrato.
Come ho detto prima, un binomio è un polinomio di due termini, che possono essere aggiunti o sottratti:
Possiamo moltiplicare questi binomi in tre modi diversi:
Una somma per una somma:
Una differenza per una differenza:
E una somma per una differenza:
I primi due casi possono essere squadrati come binomi, poiché lo stesso binomiale viene moltiplicato due volte:
Notevoli formule dei prodotti
Le formule dei prodotti più importanti sono: il quadrato di un’aggiunta, il quadrato di una sottrazione e l’aggiunta per differenza o differenza di quadrati.
Diamo un’occhiata a ciascuno di essi:
Formula del quadrato di una somma
Iniziamo con la moltiplicazione di due binomi in cui i loro termini (uguali in entrambi i binomi) vengono sommati insieme:
Stiamo moltiplicando lo stesso binomio due volte, quindi possiamo metterlo come il quadrato di una somma:
D’altra parte, se moltiplichiamo i due binomi che abbiamo:
E raggruppare i termini:
Questo prodotto notevole recita: quadrato del primo, più il doppio del primo per il secondo, più il quadrato del secondo:
Il primo è «a» (il primo termine del polinomio) e il secondo è «b» (il secondo termine del polinomio):
Per applicare questa formula è sufficiente sostituire i termini del polinomio con a e b. Per esempio:
Questo è il quadrato di una somma e noi applicheremo la sua formula per non dover eseguire la moltiplicazione.
Il primo è x e il secondo è 1. Così:
- Primo quadrato: x².
- Il doppio del primo dal secondo: 2.x.1
- Quadrato del secondo: 1².
Finora avete applicato la formula. Ora dobbiamo operare entro ogni termine per semplificare, moltiplicare i numeri e risolvere i poteri:
Un grave errore è non rendersi conto che l’espressione di cui sopra è un prodotto notevole e squadrando ogni termine in modo errato:
Formula del quadrato di una sottrazione o del quadrato di una differenza
Questa formula è molto simile alla precedente. Ecco perché è necessario fare molta attenzione a non confonderli, in quanto si differenziano in un solo segno.
In questo caso, abbiamo la moltiplicazione di due binomi in cui i loro termini (uguali in entrambi i binomi) vengono sottratti:
Questa moltiplicazione, possiamo metterla come il quadrato di una sottrazione:
Se facciamo la moltiplicazione dei binomi, ce l’abbiamo::
Si giunge così alla conclusione che il quadrato di una differenza è sempre uguale a:
È così che si legge: Quadrato del primo, meno il doppio del primo per il secondo, più il quadrato del secondo.
Come nel caso precedente, il primo è «a» (il primo termine del polinomio) e il secondo è «b» (il secondo termine del polinomio):
Per applicare questa formula è sufficiente sostituire i termini del polinomiale con a e b.
Per esempio:
Applichiamo la formula del quadrato di una sottrazione:
- Quadrato del primo: 2².
- Il doppio del primo per secondo: 2.2.2.x
- Seconda piazza: x².
Sia il quadrato di un’addizione che il quadrato di una sottrazione possono essere utilizzati per fattorizzare i polinomi, applicati al contrario, cioè dallo sviluppo, ottenendo il prodotto notevole.
Formula della somma per differenza: differenza di quadrati: differenza di piazze
La terza delle formule che andremo a vedere è trovare direttamente il risultato di una somma per differenza di binomi:
Se sviluppiamo la loro moltiplicazione, ce l’abbiamo:
Pertanto, la somma per differenza sarà pari a:
Questa formula è molto utile nella fattorizzazione dei polinomi e nella semplificazione delle frazioni algebriche quando abbiamo la sottrazione di due termini al quadrato.
Vediamo un esempio di come applicare questa formula
Il primo è x e il secondo è 1, poi:
- Primo quadrato: x².
- Il doppio del primo dal secondo: 2.2.2.x
- Quadrato del secondo: 1².
Ce l’abbiamo:
A volte, come nel factoring polinomiale, questa formula è molto utile applicata nella direzione opposta. Per esempio:
Quello che dobbiamo identificare nei polinomi di questo tipo è se si tratta o meno di una differenza di quadrati. A prima vista sembra che non perché il primo termine non è al quadrato, ma 25 lo possiamo mettere come 5²:
E ora è più chiaro che si tratta di una differenza di quadrati. Pertanto, possiamo metterlo come somma per differenza:
Da prendere in considerazione con le formule di prodotti notevoli
Ho appena mostrato le tre formule dei prodotti più importanti notevoli.
Ci sono altri prodotti notevoli o identità notevoli come il cubo di un’aggiunta, il cubo di una sottrazione, trinomio quadrato….. che non sono affatto pratici o sono più complicati da memorizzare.
In questi casi, è preferibile sviluppare la moltiplicazione dei polinomi piuttosto che memorizzare una formula.
Un’altra cosa da tenere a mente è che il primo e il secondo termine non devono essere formati da un unico fattore. Ogni termine può essere composto da diversi fattori, ad esempio:
In tal caso, fare molta attenzione e non dimenticare di quadratura di tutto il termine, con l’applicazione della proprietà del potere corrispondente
Esempi di prodotti notevoli con termini multifattoriali
Non sempre, il primo e il secondo termine di un binomio devono essere formati da un unico fattore. Ogni termine può essere composto da diversi fattori, ad esempio:
In questi casi, quando si squadrano il primo e il secondo termine, si deve tener conto di questa proprietà dei poteri:
Ciò significa che quando abbiamo una moltiplicazione elevata ad un esponente, il risultato è uguale ad ogni fattore elevato a quello stesso esponente.
Risolviamo i prodotti di cui sopra notevole per rendere tutto più chiaro per voi:
In primo luogo, identifichiamo i termini: il primo è 2y e il secondo è 3x.
Applichiamo la formula del quadrato di una sottrazione e rimane:
Ora è il momento di applicare questa proprietà quando si devono quadrare diversi fattori:
E si adatta:
Infine, semplifichiamo i termini risolvendo i poteri e moltiplicando i numeri:
Facciamo il secondo esempio:
Questa volta è il quadrato di una somma. Il primo termine è 4x² e il secondo 5y.
Applichiamo la formula:
Questa volta, quando si tratta di quadratura, entro il primo termine, ho un altro quadrato, quindi ricordatevi di moltiplicare gli esponenti:
Infine, semplifichiamo ogni termine:
Vediamo un terzo esempio con una somma per differenza:
Applichiamo la vostra formula:
Risolviamo i quadrati e semplifichiamo:
Esercizi risolti di prodotti notevoli
1 – Rende le seguenti identità notevoli: