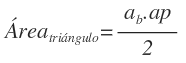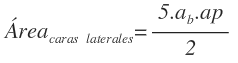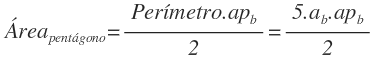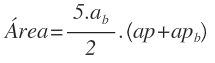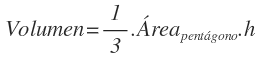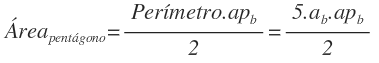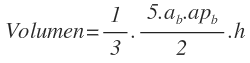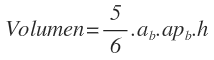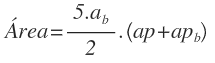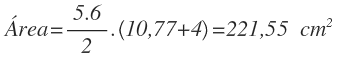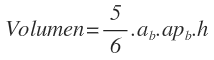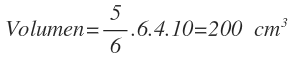A continuación te voy a explicar cómo calcular el volumen de una pirámide pentagonal regular y cómo calcular el área de una pirámide pentagonal regular Para ello, veremos qué es una pirámide pentagonal regular y sus elementos principales.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Pirámide pentagonal regular
Una pirámide pentagonal regular es una pirámide cuya base es un pentágono y sus caras laterales son triángulos isósceles que se unen en un vértice llamado ápice.
Elementos principales de una pirámide pentagonal regular
Vamos a ver detalladamente los elementos de una pirámide pentagonal regular
Aristas de una pirámide pentagonal regular
Las aristas son segmentos donde se encuentran dos caras. Tenemos dos tipos de aristas:
- Las aristas básicas, que son las aristas que están en la base
- Las aristas laterales, que van desde la base hasta el vértice
Caras de una pirámide pentagonal regular
Una pirámide pentagonal regular tiene 6 caras: 5 caras laterales, que son triángulos isósceles:
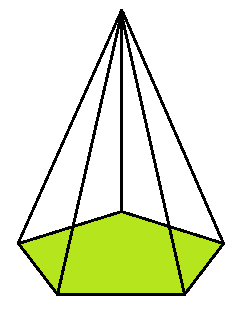
Y una base, que es un pentágono:
Altura de una pirámide pentagonal regular
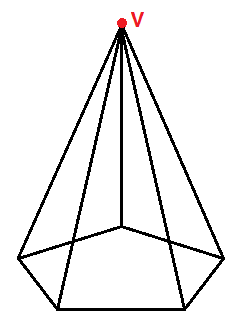
Vértice de una pirámide pentagonal regular
El vértice, también conocido como ápice, es el punto donde se unen todas las aristas laterales o todas las caras laterales. Es el punto más alto de la pirámide:
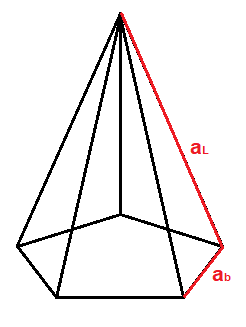
Apotema de una pirámide pentagonal regular
La apotema de la pirámide es la distancia que hay desde el vértice hasta el centro de la arista de la base:
Más abajo veremos cómo se calcula
Apotema de la base de una pirámide pentagonal regular
Cómo calcular la apotema de una pirámide pentagonal regular
Para calcular la apotema de una pirámide pentagonal regular, necesitamos conocer la altura y la apotema de la base, ya que estos dos elementos junto con la apotema de la pirámide forman un triángulo rectángulo:
Por tanto, aplicando el teorema de Pitágoras, podemos calcular el apotema:
donde h es la altura y apb es la apotema de la base.
Cómo calcular el área de una pirámide pentagonal regular
El área de una pirámide regular es igual al área de las caras laterales más el área de la base:
Como hemos visto anteriormente, las caras de una pirámide pentagonal son triángulos. El área de un triángulo es igual a la base por la altura, partido por 2. En este caso, la altura es el apotema de la pirámide y la base es la arista de la base de la pirámide:
Como tenemos 5 caras, el área de las caras laterales, es el área anterior multiplicada por 5:
Por otro lado, el área de la base es el área de un pentágono, que es igual al perímetro del pentágono por la apotema, partido por 2. En este caso, el perímetro es 5 veces la arista de la base (ya que tenemos 5 aristas) y la apotema es la apotema de la base:
El área de la pirámide pentagonal regular es la suma de las dos áreas anteriores:
Que simplificando la expresión sacando factor común nos queda:
Cómo calcular el volumen de una pirámide pentagonal regular
El volumen de una pirámide pentagonal regular es igual a un tercio del área de la base por la altura de la pirámide:
El área de la base es el área de un pentágono, que como acabamos de ver es:
Sustituimos esta expresión en la fórmula del volumen:
Y operando nos queda la fórmula del volumen de una pirámide pentagonal regular:
Ejercicios resueltos de una pirámide pentagonal regular
Calcular el área y el volumen de una pirámide pentagonal regular cuya apotema de la base es igual a 4 cm, la arista de la base es igual a 6 cm y cuya altura mide 10 cm.
Tenemos los siguientes datos:
La fórmula para calcular el área de la pirámide pentagonal es:
De esta fórmula tenemos todos los datos menos el de la apotema. Por tanto, vamos a calcular la apotema en primer lugar:
Y ahora ya podemos calcular el área:
Ahora vamos a calcular el volumen, utilizando su fórmula:
Tenemos todos los datos, por lo que sustituimos por sus valores y operamos:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: