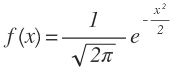A continuación veremos qué es la distribución normal estándar y cómo utilizar su tabla, con ejemplos y ejercicios resueltos paso a paso.
¡Vamos allá!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es la distribución normal estándar
Cualquier distribución normal de media μ y desviación típica σ puede asociarse a una distribución normal de media 0 y desviación típica 1. A esta distribución se le llama distribución normal estándar y se designa con N(0,1).
La fórmula de la función de la distribución normal estándar es:
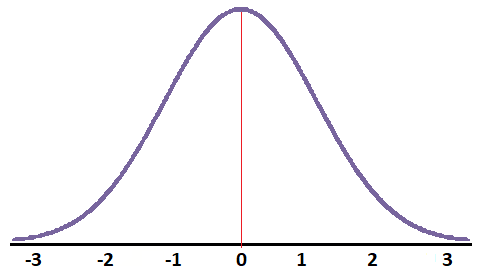
Si representamos esta función en los ejes nos queda la curva de distribución normal estándar o distribución normal N(0,1):
Donde el 0 está en el medio, ya que es la media.
Para calcular el área encerrada entre menos infinito y cualquier valor o entre dos valores, que es el porcentaje o la probabilidad, se tendría que resolver la integral correspondiente.
Por suerte, no es necesario resolver integrales para obtener el área, ya que se obtienen de la tabla de distribución normal estándar.
Tabla de distribución normal estándar N(0,1)
En la tabla de distribución normal estándar ya tenemos calculadas las áreas para muchos valores, pero hay que tener en cuenta lo siguiente:
- La tabla solo es válida para la distribución normal de media 0 y desviación típica 1, N(0,1)
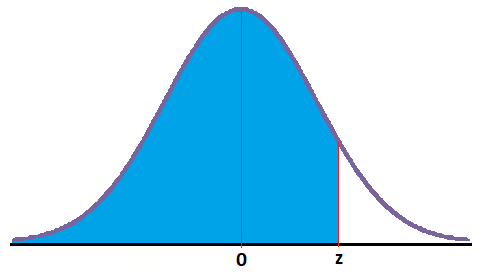
- Sólo se pueden obtener las áreas que están a la izquierda de un número positivo, es decir, el equivalente de calcular el área encerrada en la curva y el eje x, desde menos infinito a un número positivo:
El área que queda a la izquierda de z es igual a la probabilidad de que nuestro valor sea menor o igual que z y se designa como:
>> Descarga aquí tu tabla de distribución normal N(0,1) en PDF
Cómo utilizarla tabla de distribución normal estándar N(0,1)
Ya hemos visto qué es la tabla de distribución normal estándar y ahora vamos a ver cómo se utiliza. Te explicaré cómo obtener la probabilidad en cada uno de los casos que se te puedan presentar para una distribución normal N(0,1).
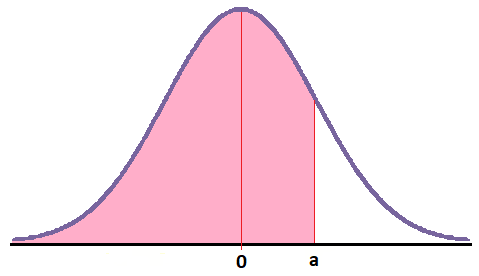
Probabilidad menor o igual que un número positivo
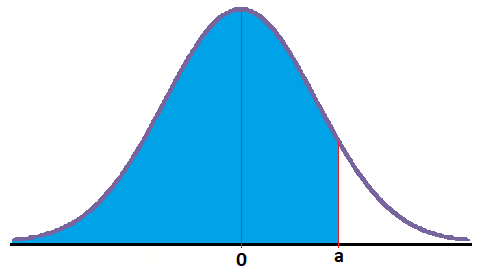
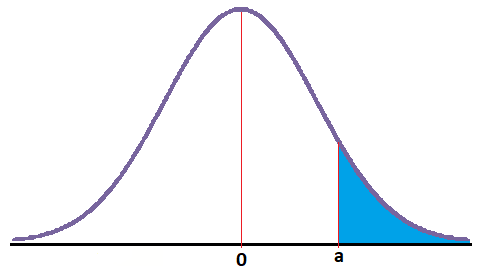
En este caso tenemos que obtener el área que queda a la izquierda de un número positivo:
Esta probabilidad puede encontrarse directamente en la tabla, ya que cumple ambos requisitos. Pero, ¿cómo se obtiene una probabilidad de la tabla?
El objetivo es formar el valor de z que queramos buscar. Para ello, tenemos que formarlo eligiendo un valor de la primera columna, que nos da la parte entera y el primer decimal, con un valor de la primera fila, que nos da el segundo decimal. El valor donde se corten será el valor de z buscado.
Ejemplo
Vamos a verlo con un ejemplo. Vamos a calcular la probabilidad P(z≤1,32):
Buscamos en la primera columna el valor 1.3 y en la primera fila el 0.02 (como ves, 1.3+0.02=1.32, que es el valor buscado). Desde el 1.3 de la primera columna nos movemos hacia la derecha hasta la columna correspondiente al 0.02. El valor obtenido es la probabilidad P(z≤1,32):
Por tanto, el área que queda a la izquierda de 1,32 es 0,9066 o lo que es lo mismo, P(z≤1,32)=0,9066, o expresado en porcentaje 90,66%.
Probabilidad mayor que un número positivo
Ahora tenemos que obtener el área que queda a la derecha de un número positivo.
Como indicamos anteriormente, la tabla de distribución normal estándar solamente nos da el valor de las áreas que quedan a la izquierda del número positivo o lo que es lo mismo, la probabilidad de los valores que son menores o iguales que z.
Entonces, ¿cómo se utiliza la tabla en este caso?
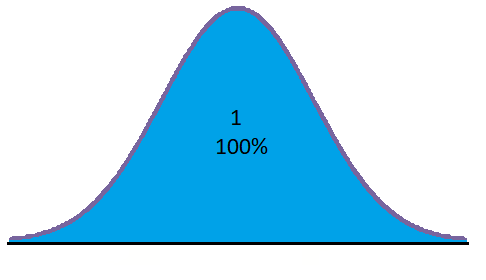
Debemos tener claro, que el área encerrada entre la curva de distribución normal y el eje x es igual a 1:
Hasta el momento solamente sabemos obtener el área que queda a la izquierda de un número, pero sabiendo que el área total es igual a 1, si sé el valor de una parte del área, puedo calcular fácilmente el área restante solo con restarle a 1 el valor del área que ya sé.
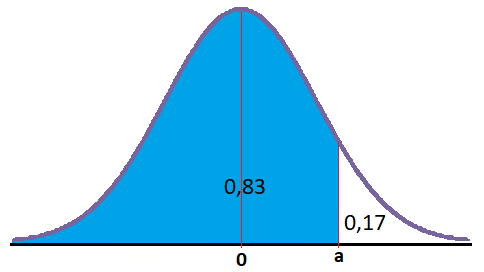
Si por ejemplo sé que el área a la izquierda de un determinado valor es igual a 0,83, el área restante será igual a 0,17, ya que 1-0,83=0,17:
Por tanto, el área que me queda a la derecha de un número positivo, es igual a 1 menos el valor del área que queda a la izquierda de un número positivo (que se obtiene directamente de la tabla):
Ejemplo
Por ejemplo, vamos a calcular el valor de P(z>0,74):
El área que queda a la derecha de 0,74 será igual a 1 menos el valor del área que queda a la izquierda de 0,74:
P(z>0,74)=1-P(z≤0,74)
Primero calculamos el valor de P(z≤0,74), es decir, el área que queda a la izquierda de 0,74. Entramos a la tabla por 0.7 en la primera columna y con 0.04 en la primera fila. El valor obtenido es P(z≤0,74)=0,7704.
Ahora, para hallar el área pedida, a 1 le restamos el valor de P(z≤0,74):
P(z>0,74)=1-P(z≤0,74)=1-0,7704=0,2296
O lo que es lo mismo, una probabilidad de 22,96%
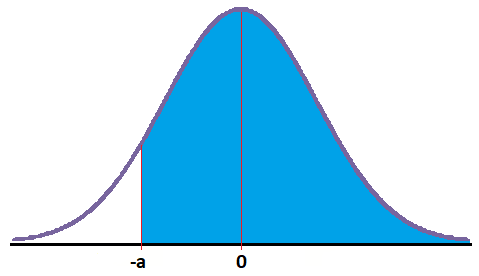
Probabilidad menor o igual que un número negativo
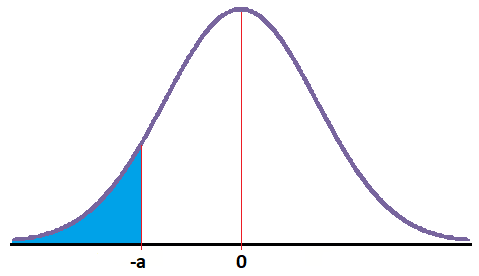
En este caso debemos obtener el área que queda a la izquierda de un número negativo:
La tabla solamente nos da el área que queda a la izquierda de un número positivo, luego no lo podemos obtener directamente.
¿Entonces cómo calculamos este caso?
La curva de la distribución normal es simétrica, por lo que el área que queda a la izquierda de un número negativo es la misma que el área que queda a la derecha de ese número en positivo:
Por tanto, volvemos a estar en el caso del área que queda a la derecha de un número positivo, así que se calcula de la misma forma:
Ejemplo
Por ejemplo, vamos a calcular el valor de P(z≤-2,26):
El área que queda a la izquierda de -2,26 es igual al área que queda a la derecha de 2,26, así que vamos a calcular ésta última.
P(z≤-2,26)=P(z>2,26)
El área que queda a la derecha de 2,26 será igual a 1 menos el valor del área que queda a la izquierda de 2,26:
P(z>2,26)=1-P(z≤2,26)
Primero calculamos el valor de P(z≤2,26), es decir, el área que queda a la izquierda de 2,26. Entramos a la tabla por 2.2 en la primera columna y con 0.06 en la primera fila. El valor obtenido es P(z≤2,26)=0,9881.
Ahora, para hallar el área pedida, a 1 le restamos el valor de P(z≤2,26):
P(z>2,26)=1-P(z≤2,26)=1-0,9881=0,0019
Que es igual al área que queda a la izquierda de -2,26:
P(z≤-2,26)=P(z>2,26)=0,0019
O lo que es lo mismo, una probabilidad de 0,19%
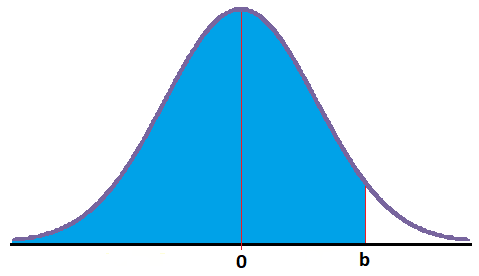
Probabilidad mayor que un número negativo
En este caso debemos obtener el área que queda a la derecha de un número negativo:
No podemos obtenerla directamente de la tabla.
Igual que antes, nos aprovechamos de que la curva es simétrica y por tanto, el área que queda a la derecha de un número negativo es igual al área que queda a la izquierda de ese número en positivo:
Por tanto, estamos en el caso de calcular el área que queda a la izquierda de un número positivo, que se calcula directamente de la tabla:
Ejemplo
Por ejemplo, vamos a calcular el valor de P(z>-1,73):
El área que queda a la derecha de -1,73 es igual al área que queda a la izquierda de 1,73, así que vamos a calcular ésta última.
P(z>-1,73)=P(z≤1,73)
Para calcular P(z≤1,73), entramos a la tabla en la primera columna con 1.7 y en la primera fila con 0.03 obteniendo un valor de 0,9582. Por tanto:
P(z>-1,73)=P(z≤1,73)=0,9582
O lo que es lo mismo, una probabilidad de 95,82%
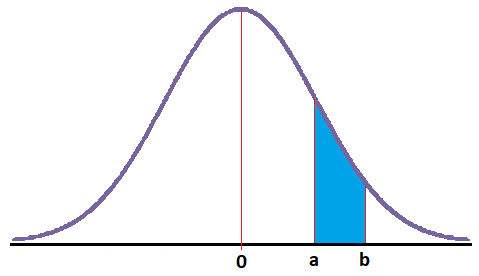
Probabilidad entre dos números positivos
En este caso nos piden el área encerrada entre la curva y dos números positivos:
Para calcular este área, primero obtenemos directamente de la tabla el área encerrada a la izquierda del número mayor (b):
Después calculamos el área encerrada a la izquierda del número menor (a), también directamente de la tabla:
El área resultante de restar ambas áreas será el área encerrada entre la curva y ambos números positivos.
Por tanto, el área encerrada entre dos números positivos es igual al área encerrada a la izquierda del número mayor menos el área encerrada a la izquierda del número menor:
Ejemplo
Por ejemplo, vamos a calcular el valor de P(0,47<z≤2,13):
Primero calculamos el valor del área encerrada a la izquierda de 2,13 directamente de la tabla:
P(z≤2,13)=0,9834
Calculamos ahora el área encerrada a la izquierda de 0,47:
P(z≤0,47)=0,6808
Y restamos ambas áreas:
P(0,47<z≤2,13)=P(z≤2,13)-P(z≤0,47)=0,9834-0,6808=0,3026
Por tanto, el área encerrada entre 2,13 y 0,47 es igual a 0,3026, o lo que es lo mismo, a una probabilidad de 30,26%.
Probabilidad entre dos números negativos
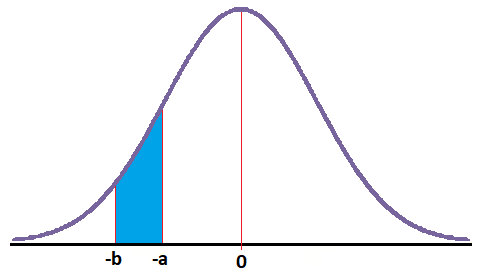
En este caso nos piden el área encerrada entre la curva y dos números negativos:
Este caso, lo vamos a calcular aplicando la simetría de la curva normal. Entonces, el área encerrada entre dos números negativos es igual que el área encerrada entre esos mismos números en positivo:
Por tanto, se calcula igual que el caso anterior, pasando previamente los números a positivo:
Ejemplo
Por ejemplo, vamos a calcular el valor de P(-1,77<z≤-0,65):
En primer lugar pasamos los números a positivo, teniendo en cuenta que el -1,77 que era el número menor, en positivo pasa a ser el mayor y el -0,65, que era el número mayor, pasa a ser el menor al pasarlo a positivo:
P(-1,77<z≤-0,65)=P(0,65<z≤1,77)
Ahora calculamos el área entre los números positivos:
P(z≤1,77)=0,9616
P(z≤0,65)=0,7422
Y al área mayor le restamos el área menor:
P(0,65<z≤1,77)=P(z≤1,77)-P(z≤0,65)=0,9616-0,7422=0,2194
Y el área encerrada entre dos números negativos es la misma que los dos números en positivo:
P(-1,77<z≤-0,65)=P(0,65<z≤1,77)=0,2194
O en probabilidad, un 21,94%.
Probabilidad entre un número negativo y un número positivo
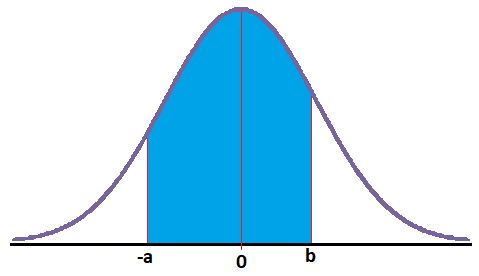
En este caso tenemos que obtener el área encerrada entre un número negativo y un número positivo:
Para calcularla, primero tenemos que calcular el área encerrada a la izquierda del número positivo (b), directamente de la tabla:
Después calculamos el número que queda a la izquierda del número negativo:
Pero en este caso, no es posible hacerlo directamente con la tabla, pero lo calculamos igual que hemos hecho anteriormente en el apartado de «Probabilidad menor o igual que un número negativo», es decir, aplicando simetría:
Y el área será igual a 1 menos el área encerrada a la izquierda del número:
Por tanto, el área encerrada entre un número negativo y otro positivo es igual al área encerrada a la izquierda del número positivo, menos el área que queda a la izquierda del número negativo:
Ejemplo
Por ejemplo, vamos a calcular el valor de P(-1,27<z≤1,66):
Primero calculamos el valor del área encerrada a la izquierda de 1,66 directamente de la tabla:
P(z≤1,66)=0,9515
Calculamos ahora el área encerrada a la izquierda de -1,27, teniendo en cuenta la explicación anterior:
P(z≤-1,27)=1-P(z≤1,27)=1-0,8980
Y restamos ambas áreas:
P(-1,27<z≤1,66)=P(z≤1,66)-P(z≤-1,27)=
=0,9515-(1-0,8980)=0,9515-1+0,8980=0,8495
O lo que es lo mismo, a una probabilidad de 84,95%.
Cómo calcular el valor de z conocida la probabilidad
Vamos a ver ahora cómo obtener el valor de z si conozco el porcentaje o la probabilidad, es decir, conozco un valor de dentro de la tabla y tengo que hallar a qué valor de z pertenece.
Valores de z para probabilidades mayores que 0,5
Por ejemplo, ¿qué valor de z tiene un área a su izquierda igual a 0,975?
Me voy a la tabla y busco dentro el valor 0,975 y a partir de ese valor, me muevo hacia la izquierda para encontrar el valor entero y el primer decimal de z (1,9) y hacia arriba para encontrar el segundo decimal (0,06), por lo que el valor que deja a su izquierda un área igual a 0,975 es z=1,96:
Si no encuentro el valor exactamente, puedo tomar el valor más próximo si se acerca mucho o tomar una media entre dos valores.
Por ejemplo para un valor de 0,9 puedo tomar el valor de 0,8997 que corresponde a una z de 1,28.
Para un valor de 0,95, no está pero encuentro el 0,9495 y el 0,9505, que corresponde a los valores de z de 1,64 y 1,65 respectivamente, por lo que me quedo con el valor que se queda en medio z=1,645.
Valores de z para probabilidades menores que 0,5
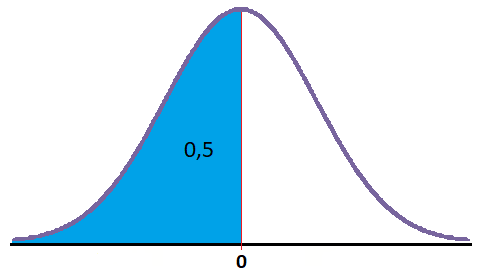
Si te das cuenta, el valor 0,5 corresponde a un z=0, ya que es justo el medio de la curva y el área encerrada es justo la mitad:
Por tanto, cuando las probabilidades son menores que 0,5,es porque el valor de z es negativo.
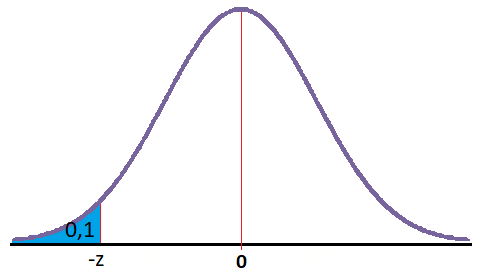
Por ejemplo, ¿a qué valor de z corresponde una probabilidad del 10%?
Tenemos que encontrar un valor de z que deje a su izquierda un área igual a 0,1:
Ya sabemos que z será negativo y no lo podemos obtener directamente de la tabla, pero como sabemos, por simetría tendríamos el área que queda a la derecha de z y si este área es igual a 1 menos el área que queda a la izquierda de este valor de z.
Que despejando, llegamos a la conclusión de que debe ser igual a 0,9:
Buscamos el valor de z que sea igual a 0,9 en la tabla. Tenemos cerca 1,28 y 1,29, por lo que cogemos el valor medio, es decir, z=1,285:
El área que queda a la izquierda de 1,285 es igual a 0,9, por lo que el área que queda a la derecha de 1,285 será igual a 0,1 y por tanto, por simetría, el área que queda a la izquierda de -1,285 será igual a 0,1.
Como nos preguntan por el área que queda a la izquierda de un determinado valor, nuestro valor de z buscado es z=-1,285:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: