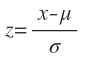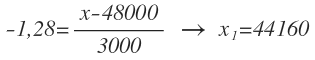En esta lección te voy a explicar qué es el intervalo de confianza y veremos cómo se calcula utilizando la tabla N(0,1), con ejemplos y ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es el intervalo de confianza
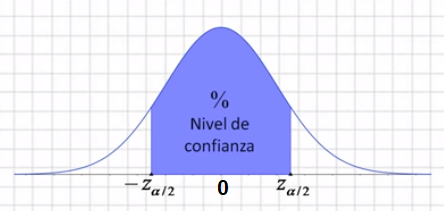
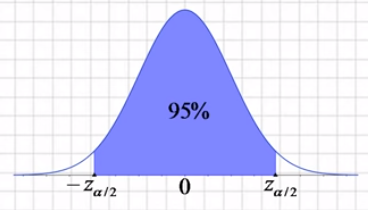
El intervalo de confianza es encontrar dos valores simétricos respecto a la media (que una distribución normal estándar N(0,1) la media es 0), entre los cuales encierren un porcentaje que yo quiera conocer, llamado nivel de confianza:
Como puedes observar en la imagen anterior a los dos valores simétricos son -z de α/2 y z de α/2:
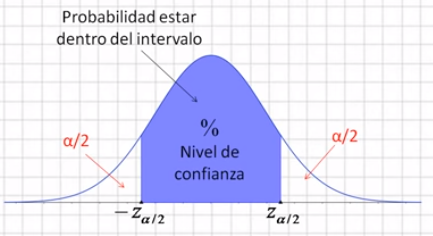
El área encerrada entre -z de α/2 y z de α/2 es la probabilidad de estar dentro del intervalo de confianza y por tanto, también hay un área que queda fuera de ese intervalo, llamada nivel de significación (α).
Es decir, el nivel de significación es la probabilidad de quedar fuera del nivel de confianza. El área será igual a 1 menos el nivel de confianza:
O si lo calculamos con porcentajes sería:
Y esa área se reparte entre el área que queda a la derecha del nivel de confianza y la que queda a la izquierda del nivel de confianza, quedando a cada lado un área igual a α/2 y de ahí el nombre de -z de α/2 y z de α/2:
Cómo calcular el intervalo de confianza con la tabla N(0,1)
Vamos a ver ahora cómo se calcula el intervalo de confianza.
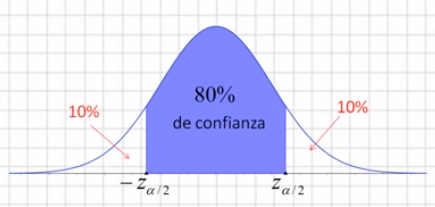
Por ejemplo, supongamos que nos piden calcular entre qué dos variables se encuentra el 80% de una determinada muestra:
Si tengo un 80% de confianza, sé que se queda fuera un 20% o lo que es lo mismo α=20%:
α=100-% Nivel de confianza=100-80=20%
Por lo que α/2=10%, que es el valor que queda a cada lado del nivel de confianza del 80%:
Entendido esto, vamos a ver cómo utilizar la tabla N(0,1) para calcular el intervalo de confianza.
La tabla no me da la posibilidad de conocer la probabilidad que hay entre dos valores, sólo me da la posibilidad de obtener el área que queda a la izquierda de un cierto valor:
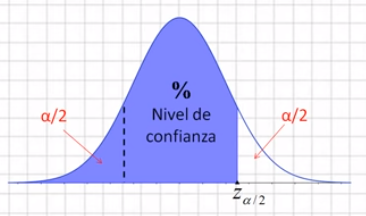
Pero el área que queda a la izquierda de un cierto valor es igual al nivel de confianza más el área α/2 que queda a la izquierda del nivel de confianza:
Por tanto, conocido el nivel de confianza, puedo buscar en la tabla N(0,1) un valor que deje a su izquierda el nivel de confianza más α/2 y ese será el valor positivo del intervalo de confianza (z de α/2). Su simétrico con respecto a 0 (-z de α/2) será ese mismo valor pero en negativo.
Por ejemplo, vamos a calcular el intervalo de confianza del 95%.
Me piden que encuentre dos valores entre los cuales queda encerrada una probabilidad del 95%, es decir, que su área sea igual a 0,95:
Calculamos el área que se queda fuera del nivel de confianza:
α=100-95=5%
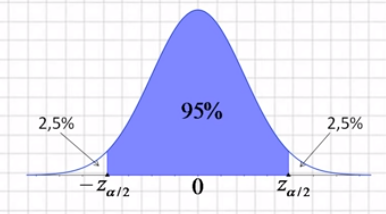
Y ese 5% se reparte por igual a ambos lados del intervalo de confianza, es decir, 2,5% a su izquierda y 2,5% a su derecha:
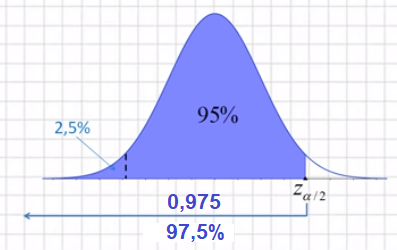
Por tanto, en la tabla, tengo que buscar un valor z que a su izquierda deje un porcentaje de 95%+2,5%=97,5%, es decir, un área igual a 0,975:
Por lo tanto, me voy a la tabla, busco dentro el 0,975 y a partir de ese valor, me muevo hacia la izquierda para encontrar el valor entero y el primer decimal de z (1,9) y hacia arriba para encontrar el segundo decimal (0,06), por lo que el valor que deja a su izquierda un área igual a 0,975 es z=1,96:
z=1,96 es el valor positivo del intervalo de confianza, por lo que el valor negativo será z=-1,96.
Por tanto, el intervalo de confianza que me están pidiendo es:
Vamos a ver otro ejemplo. Vamos a calcular el intervalo de confianza del 90%.
Si el nivel de confianza es igual al 90%, el porcentaje que queda fuera es:
α=100-90=10%
Y por tanto α/2=5%
Tengo que buscar en la tabla el valor de z que deje a su izquierda un porcentaje de 90%+5%=95%, o lo que es lo mismo, un área igual a 0,95.
Me voy a la tabla y busco el 0,95. No encuentro el 0,95, pero encuentro el 0,9495 y el 0,9505, que corresponde a los valores de z de 1,64 y 1,65 respectivamente, por lo que me quedo con el valor que se queda en medio z=1,645.
El valor negativo será z=-1,645 y el intervalo de confianza pedido es:
Ejercicios resueltos del intervalo de confianza
Vamos a resolver un ejercicio aplicando todo lo que acabamos de ver:
La duración en kilómetros de los neumáticos de una determinada marca se ajusta a una distribución N(48000,3000). Calcula el intervalo de confianza del 80%.
En primer lugar calculamos el intervalo de confianza del 80% para una distribución normal estándar N(0,1):
α=100-80=20%
α/2=10%
Tengo que buscar en la tabla el valor de z que me dé un porcentaje de 90%. El valor más próximo que encuentro es z=1,28 (no es encontrar siempre justo el valor exacto, con un valor muy aproximado también vale).
Por tanto, el intervalo de confianza para una distribución normal N(0,1) es:
Los valores del intervalo los tengo que destipificar para convertirlos a valores de una distribución N(48000,3000):
Utilizo la fórmula de la tipificación:
Destipifico z=-1,28, susittuyendo este valor en la fórmula junto con el de la media y la desviación típica y despejando la x:
Hago lo mismo con z=1,28:
El intervalo de confianza del 80% para la distribución normal N(48000,3000) es:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: