A continuación vamos a ver cómo obtener la perpendicular común a dos rectas que se cruzan en el sistema diédrico. Dos rectas se cruzan cuando nunca llegan a cortarse, por encontrarse en planos distintos y además, no son paralelas entre ellas.
El hecho de que no sean paralelas entre ellas hace que dependiendo el punto de cada recta que tomemos, la distancia entre ellas sea distinta. Te explicaré también cómo hallar la mínima distancia entre dos rectas que se cruzan en el sistema diédrico.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Procedimiento para obtener la perpendicular común entre dos rectas que se cruzan
Para que puedas entender mejor cómo obtener la perpendicular común a dos rectas que se cruzan en el sistema diédrico, antes vamos a ver en un esquema en tres dimensiones cuál es el procedimiento general, para después dar los mismos pasos en diédrico.
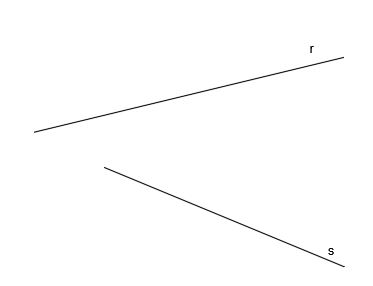
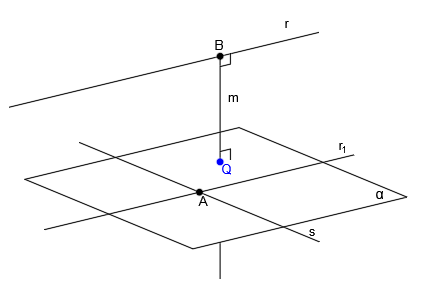
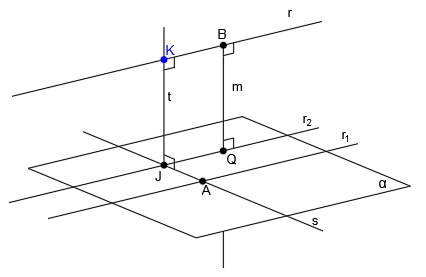
Tenemos en el espacio la recta r y la recta s, que son dos rectas que se cruzan, es decir, son dos rectas que se encuentran en distinto plano, que no son paralelas entre ellas y que nunca llegan a cortarse:
Vamos a obtener una recta que sea perpendicular las rectas r y s.
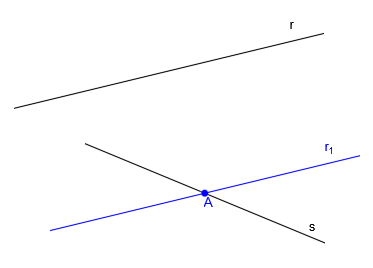
Empezamos trazando una paralela a la recta r (recta r1) por un punto cualquiera de la recta s (punto A):
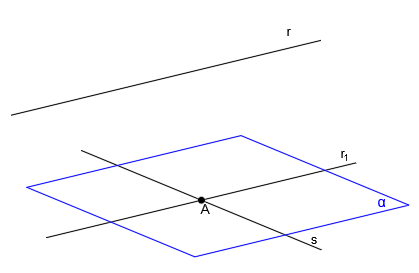
Esto lo hemos hecho para ahora poder crear el plano α a partir de las rectas r1 y s:
Este plano α, además de contener a la recta s, es paralelo a la recta r.
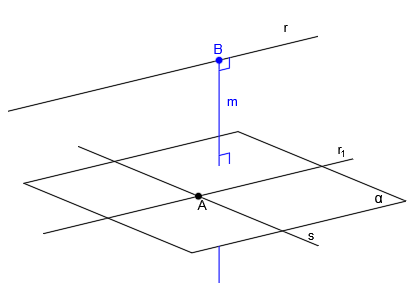
Ahora trazamos una recta perpendicular al plano α (recta m), que pase por un punto cualquiera de la recta r (punto B):
Esta recta m, al ser perpendicular al plano α, ya es perpendicular a la recta r y a la recta s (ya que el plano α lo hemos creado a partir de ambas rectas) pero tan sólo corta a la recta r y lo que queremos es que la perpendicular corte también a la recta s.
Por tanto, ahora vamos a buscar el punto donde la perpendicular corte a la recta s.
La recta m corta al plano α en el punto Q:
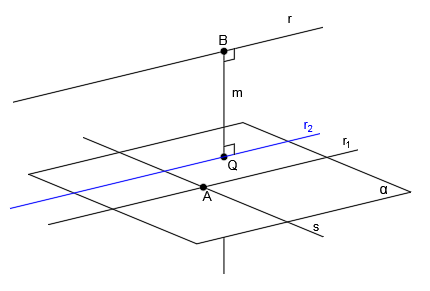
Por el punto Q, trazamos una recta paralela a r1 (recta r2):
Si te das cuenta, la recta m es una perpendicular común a la recta r y a la recta r2, que corta a ambas rectas en los puntos B y Q. Eso es lo que buscamos con las rectas r y s.
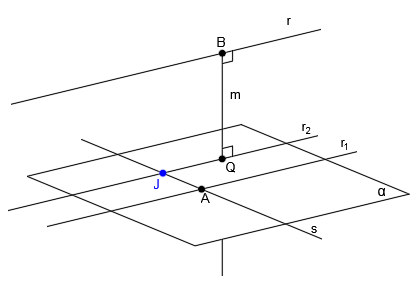
La recta r2 corta a la recta s en el punto J:
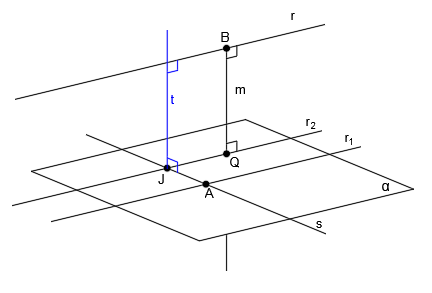
Por el punto J, trazamos una recta paralela a m (recta t):
La recta t corta a la recta r en el punto K:
La recta t, es perpendicular a la recta s y a la recta r y además corta a las dos rectas, por lo que la recta t es la perpendicular común que estábamos buscando.
Mínima distancia entre dos rectas que se cruzan
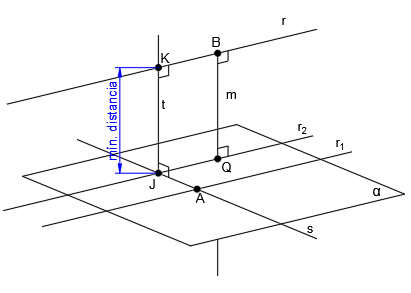
Una vez tenemos la perpendicular común entre dos rectas que se cruzan, ya podemos obtener la mínima distancia entre las dos rectas.
La mínima distancia entre dos restas que se cruzan es igual a la distancia entre los puntos de corte de la perpendicular con cada recta, es decir, siguiendo con el esquema del apartado anterior, sería la distancia entre los puntos J y K:
Perpendicular común en diédrico a dos rectas que se cruzan en diédrico
Una vez tenemos claro el procedimiento para hallarla perpendicular común a dos rectas que se cruzan, vamos a realizar los mismos pasos, pero aplicados al sistema diédrico y dando los pasos intermedios que necesitemos para alcanzar cada paso.
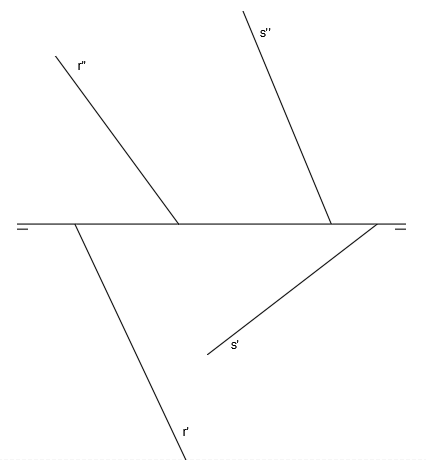
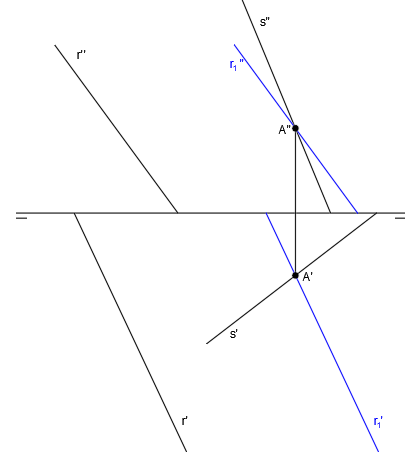
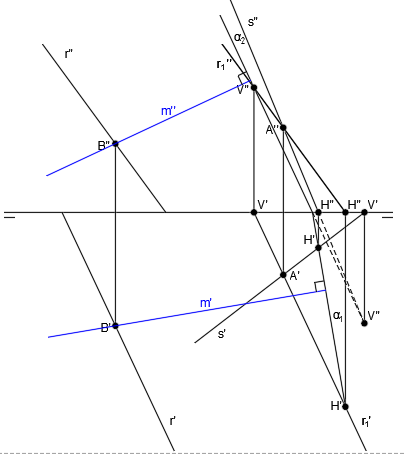
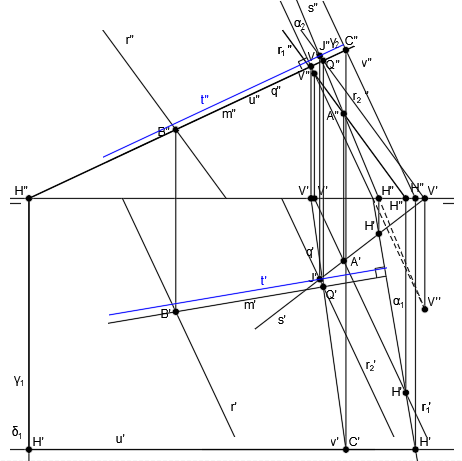
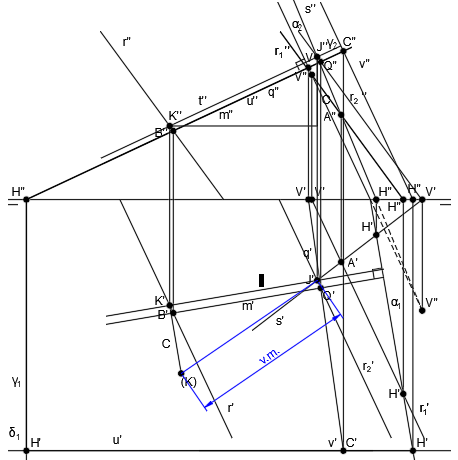
Tenemos la rectas r y s representadas en el sistema diédrico, que son dos rectas que se cruzan:
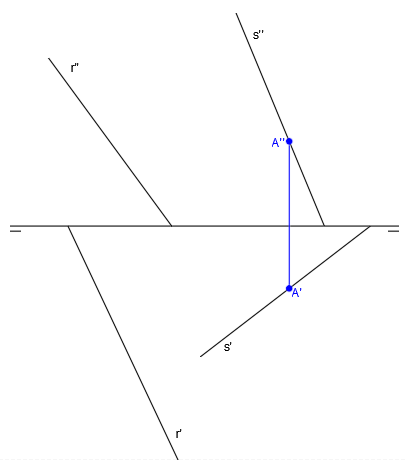
Tomamos un punto cualquiera de la recta s, que será el punto A:
Por el punto A, trazamos una recta paralela a r, que es r1:
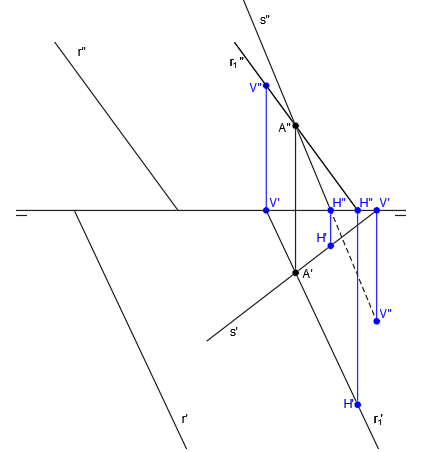
Ahora vamos a crear un plano a partir de las rectas s y r1, es decir, crearemos un plano a partir de dos rectas que se cortan.
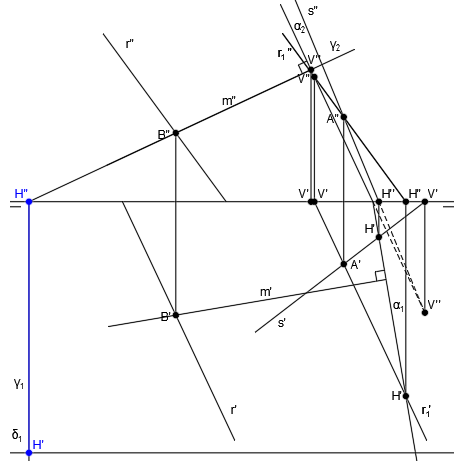
Para ello, hallamos las trazas de cada una de las rectas:
Y representamos la traza vertical del plano, α2, uniendo las trazas V” de las rectas y la traza horizontal del plano, α1, uniendo las trazas H’ de las rectas:
Ya tenemos el plano α, que contiene a la recta s, es paralelo a la recta r.
Ahora tomamos un punto cualquiera de la recta r (punto B):
Y trazamos una recta perpendicular al plano α que pase por el punto B:
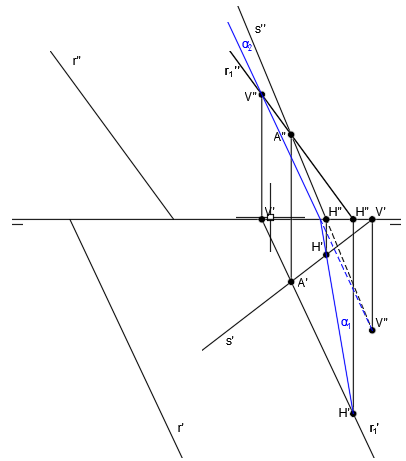
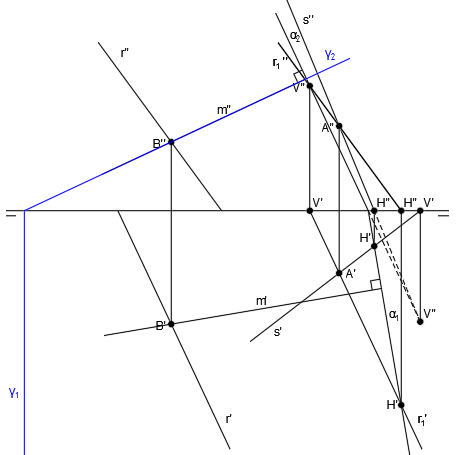
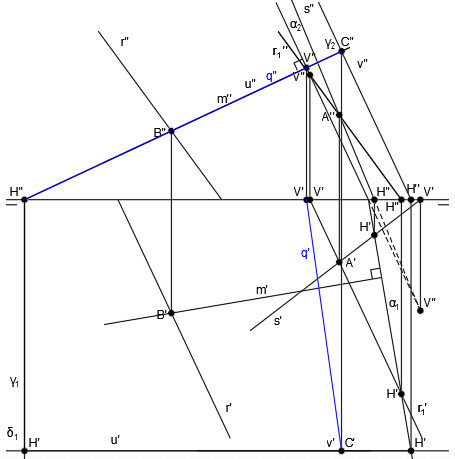
Ahora vamos a hallar la intersección entre la recta m y el plano α.
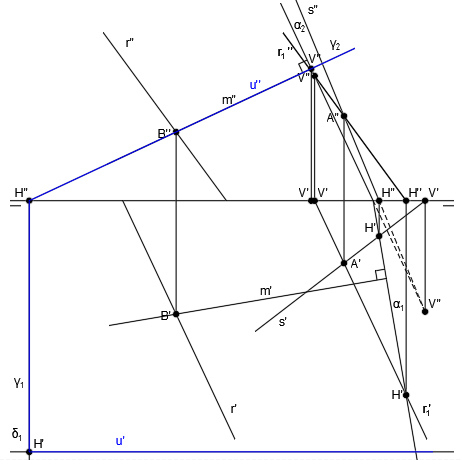
Empezamos trazando un plano auxiliar proyectante del plano vertical, que contenga a la recta m:
El punto donde se cortan las trazas verticales de los planos α2 y γ2, será la traza vertical de la recta intersección V’-V”:
Las trazas horizontales de los planos α y γ no se cortan dentro del papel, por lo que hay que seguir el procedimiento de la intersección entre dos planos cuyas trazas horizontales no se cortan en el papel.
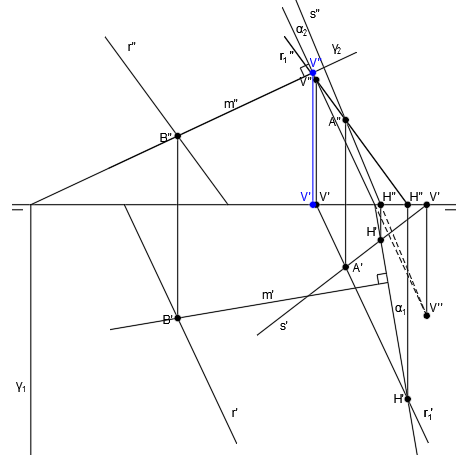
En primer lugar, dibujamos un plano horizontal auxiliar frontal en el plano horizontal:
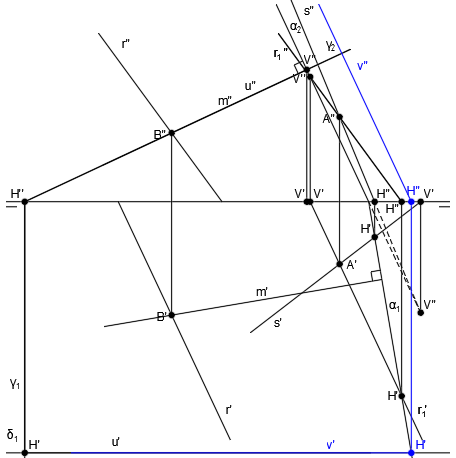
El punto donde se cortan las trazas horizontales de los planos γ1 y δ1, será la traza horizontal de la recta intersección H’-H”:
El resultado de la intersección de los planos γ y δ es la recta vertical u:
El resultado de la intersección de los planos α y δ es la recta vertical v:
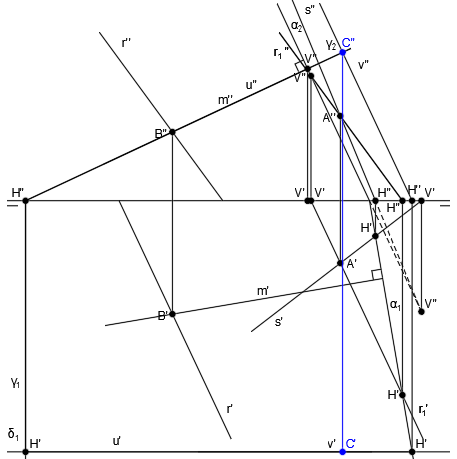
El punto de corte de u” y v” es C” y trazamos una vertical hasta u’ y v’ para obtener C’:
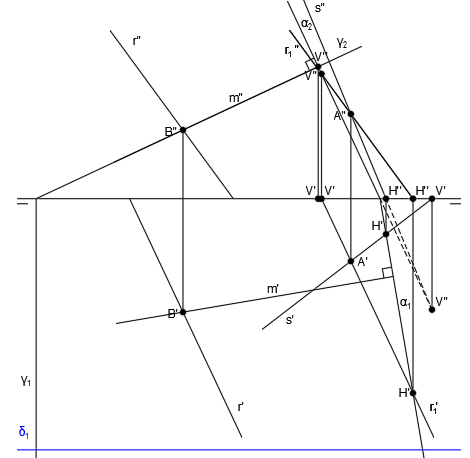
Por último, unimos V” y C” para trazar q” y C’ y V’ para trazar q’, siendo q la recta intersección entre los planos α y γ:
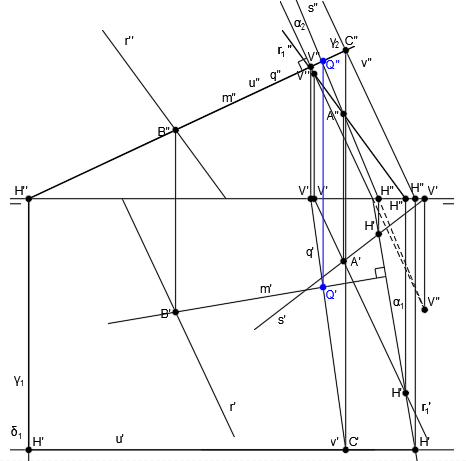
El punto de corte de la recta q y la recta m, será el punto Q, que será también el punto intersección entre la recta m y el plano α:
Seguimos.
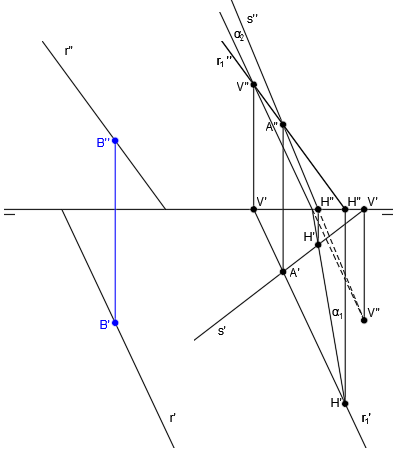
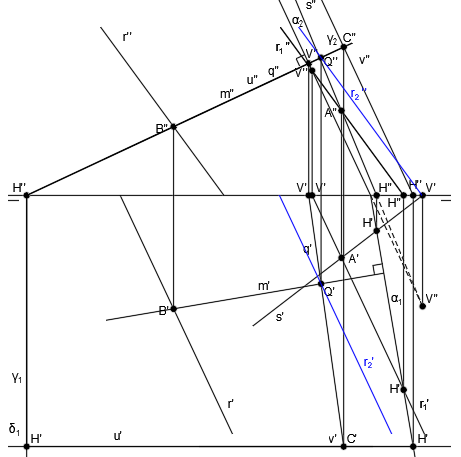
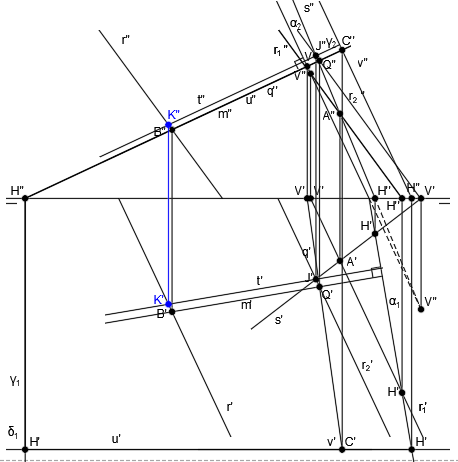
Por el punto Q, trazamos una paralela a la recta r1, que será la recta r2:
El punto de corte de la recta s y la recta r2, da como resultado el punto J:
Trazamos la recta t, que es paralela a la recta m y pasa por el punto J:
Siendo t finalmente la recta perpendicular común a la recta r y a la recta s, que es lo que queríamos encontrar.
Cómo hallar la mínima distancia entre dos rectas que se cruzan en diédrico
Ahora vamos a ver cómo obtener la mínima distancia entre dos rectas que se cortan.
Para hallar la mínima distancia, antes hay que obtener la perpendicular común a ambas rectas, por lo que hay que seguir el procedimiento descrito en el apartado anterior.
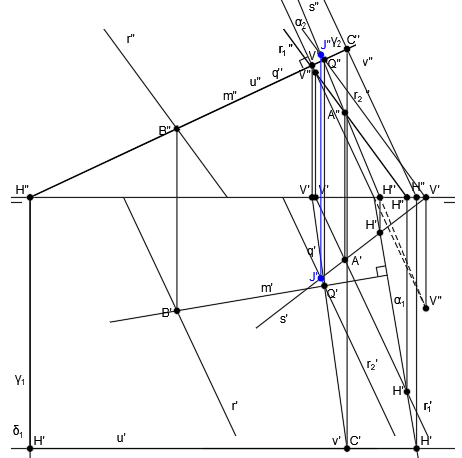
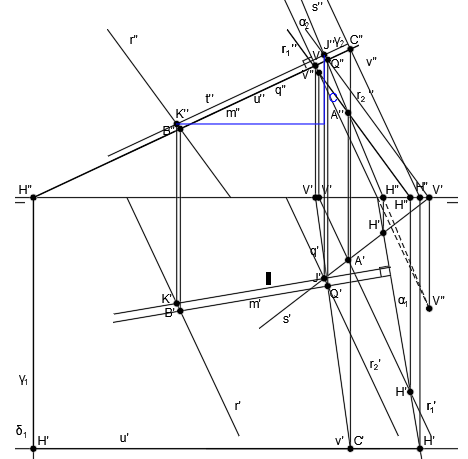
Una vez tenemos la recta t, perpendicular a ambas rectas, obtenemos el punto de corte de la recta t y la recta r, que es el punto K:
La mínima distancia entre las rectas r y s será la verdadera magnitud entre esos los puntos J y K.
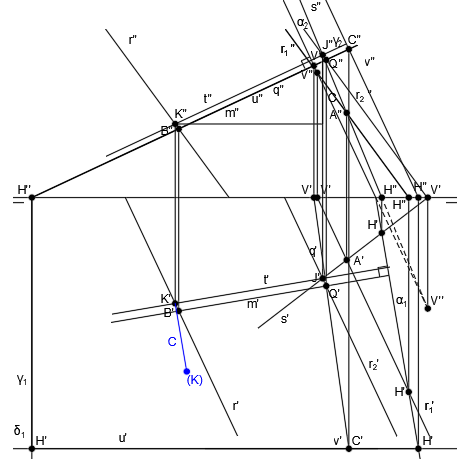
Por tanto, hallamos la diferencia de cotas en el plano vertical (C):
En el plano horizontal, desde K’, trazamos una línea perpendicular a t’, de longitud C, dando lugar al segmento K'(K):
Y finalmente, unimos los puntos J’ y (K). La distancia de dicho segmento corresponde a la verdadera magnitud entre el punto J y el punto K, o lo que es lo mismo, la mínima distancia entre la recta r y la recta s:
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE