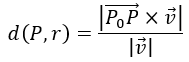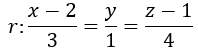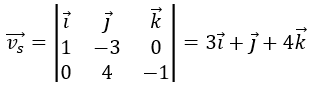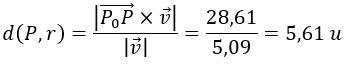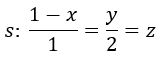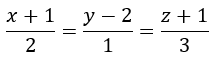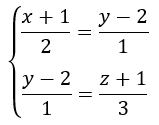En esta lección te voy a explicar cómo calcular la distancia entre dos rectas en el espacio, ya sean rectas paralelas, rectas que se cruzan, secantes o coincidentes. Con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Distancia entre dos rectas en el espacio (R3)
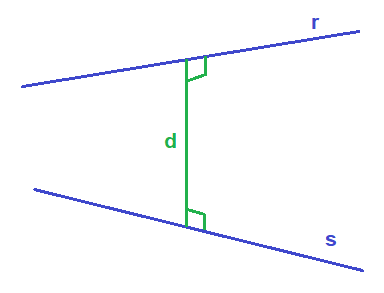
Cuando hablamos de distancia entre dos rectas en el espacio nos referimos a la distancia más corta que existe entre cualquier punto de las dos rectas, es decir, es la longitud del segmento que corta ambas rectas y además es perpendicular a ellas:
El cálculo de la distancia entre dos rectas depende de su posición relativa:
- Si las rectas son coincidentes, la distancia entre las rectas es igual a cero, ya que realmente se trata de la misma recta
- Si la rectas se cortan en un punto, la mínima distancia que existe entre ellas también es cero, ya que la mínima distancia corresponde con el punto de corte.
- En el caso de que las rectas sean paralelas, la distancia entre ellas la podemos calcular como la distancia de un punto a una recta, eligiendo un punto cualquiera de una de las rectas y calculando la distancia de ese punto a la otra recta
Y se utiliza la fórmula de la distancia de un punto a una recta:
- Si las rectas se cruzan, la mínima distancia entre ellas se calcula con la siguiente fórmula:
En los siguientes apartados, veremos cómo calcular la distancia entre dos rectas paralelas y dos rectas que se cortan y por tanto, cómo aplicar su correspondiente fórmula.
Cómo calcular la distancia entre dos rectas paralelas en el espacio (R3)
Vamos a ver un ejemplo de cómo calcular la distancia entre dos rectas paralelas en el espacio.
Tenemos las siguientes rectas r y s:
El primer paso es obtener la posición relativa de las rectas, para comprobar que se trata de rectas paralelas.
De la ecuación en forma continua de la recta r:
Obtenemos directamente un punto perteneciente a la recta y su vector de dirección:
De la recta s:
Obtenemos su vector de dirección a partir del producto vectorial de los vectores normales de los planos que forman la recta:
El vector de dirección de la recta s es:
En este caso, los vectores de dirección de la recta r y s son iguales, lo que quiere decir que las rectas r y s son paralelas:
Una vez que hemos comprobado que las rectas son paralelas, podemos calcular la distancia entre ellas como la distancia de un punto de una de las rectas a la otra recta, utilizando la fórmula de la distancia de un punto a una recta:
Elegiremos un punto perteneciente a la recta s y calcularemos la distancia de ese punto a la recta r, que ya tenemos un punto de la recta y su vector de dirección.
Para obtener un punto que pertenezca a la recta s, establecemos el valor de z en 0 en la ecuación de la recta s:
De la segunda ecuación:
Despejamos «y»:
En la primera ecuación, sustituimos «y» por su valor:
Y operamos para obtener el valor de x:
Una vez concidos los valores de x e «y» cuando z=0, podemos decir que las coordenadas del punto P que pertenece a la recta s son:
Ahora vamos a aplicar fórmula de la distancia de un punto a una recta:
Obtenemos el vector P0P:
Realizamos el producto vectorial de los vectores P0P y v
Hallamos el módulo del producto vectorial:
Hallamos el módulo del vector de dirección de la recta r:
Sustituimos ambos módulos por su valor en la fórmula y operamos:
Cómo calcular la mínima distancia entre dos rectas que se cruzan en el espacio (R3)
Vamos a ver cómo calcular la mínima distancia entre dos rectas que se cruzan en el espacio.
Tenemos dos rectas r y s:
El vector director de la recta r y un punto cualquiera de la recta r son:
El vector director de la recta s y un punto cualquiera de la recta r son:
La fórmula para calcular la mímina distancia entre dos rectas que se cruzan r y s se es:
donde:
es el valor absoluto del producto mixto de los vectores directores de r y s y el vector definido por los puntos de las rectas, y:
es el módulo del producto vectorial de los vectores de dirección de cada recta.
Otro procedimiento para calcular la mínima distancia entre dos rectas que se cruzan es hallar la recta perpendicular común a las rectas r y s, con el fin de obtener los puntos de corte Pr y Ps y después hallar la distancia entre esos dos puntos.
Ejercicios resueltos sobre distancia entre dos rectas en el espacio
Ejercicio 1
Hallar la mínima distancia entre las siguientes rectas:
En primer lugar, debemos obtener la posición relativa de ambas rectas, o dicho de otra forma, debemos determinar si se trata de dos rectas secantes, paralelas, coincidentes o cruzadas.
Tenemos las ecuaciones paramétricas de la recta r:
De donde podemos obtener directamente un punto y su vector de dirección:
Con el punto y el vector director, expresamos la ecuación contínua de la recta r:
Igualando miembros dos a dos:
Operamos y simplificamos, obteniendo las ecuaciones implícitas de la recta r:
La ecuación de la recta s es:
Las expresamos adecuandamente en su forma continua:
y poder obtener así un punto y su vector de dirección:
Teniendo los dos vectores de dirección podemos saber que las rectas no son paralelas, ya que los vectores no son proporcionales, pero no sabemos si son secantes o se cruzan, luego no queda más remedio que estudiar sus posición para saberlo.
Igualamos los miembros dos a dos:
Operamos y simplificamos, obteniendo las ecuaciones implícitas de la recta s:
Para estudiar la posición relativa de ambas rectas, formamos un sistema de 4 ecuaciones con las ecuaciones implícitas de las dos rectas:
La matriz de los coeficientes es:
Y la matriz ampliada es:
Calculamos el rango de la matriz de los coeficientes. La mayor submatriz cuadrada contenida en esta matriz es de orden 3. Elegimos la formada por las tres primeras columnas y las tres primeras filas, cuyo determinante es:
que es distinto de cero. Por tanto, su rango es igual a 3:
Calculamos ahora el rango de la matriz ampliada. Su determinante es:
que también es distinto de cero, así que, su rango es igual a 4:
Como el rango de A es igual a 3 y el rango de A* es igual a 4, las rectas se cruzan:
Como las rectas se cruzan, utilizamos la fórmula para calcular la mímina distancia entre dos rectas que se cruzan:
Empezamos calculando el producto mixto:
Para ello, antes obtenemos el vector formado por los puntos de las rectas:
Obtenemos el producto mixto de los tres vectores:
Su valor absoluto es:
Calculamos ahora el producto vectorial de los vectores de dirección:
Cuyo módulo es:
Por último, sustituimos en la fórmula y operamos:
Por tanto, la mínima distancia entre las rectas r y s es de 0,06 unidades.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: