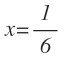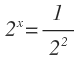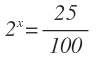¿Quieres aprender cómo resolver logaritmos? ¿Qué es un logaritmo? ¿Y un logaritmo neperiano? ¿Cómo se aplica su fórmula?
A continuación te voy a explicar no sólo cómo resolver logaritmos, sino que te explicaré qué es un logaritmo y un logaritmo neperiano. Lo iremos viendo paso a paso, con varios ejemplos para que vayas asimilando mejor el concepto.
Para entender los logaritmos, es muy importante que domines las potencias perfectamente, por lo que si no es así, te recomiendo que consultes el Curso de Potencias.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
En este vídeo encontrarás ejercicios resueltos de cómo resolver logaritmos:
Y a partir de aquí tienes explicado todo lo que necesitas saber
Qué es un logaritmo
El logaritmo de un número, es la forma de calcular el exponente al que tendría que estar elevada una base para obtener dicho número:
Es decir, es la forma de calcular el exponente «x», de la base «a» para que nos dé el número «b».
Conocidos la base «a» y el número «b», al ponerlo en forma de logaritmo, podemos calcular el exponente «x»:
Por tanto, por definición, la fórmula de los logaritmos es la siguiente:
No es una fórmula muy intuitiva. A la izquierda tenemos la forma logarítmica y a la derecha la forma exponencial.
La base del logaritmo, a, debe ser siempre positiva y no puede ser igual a 1:
Además, sólo existen los logaritmos de números positivos, por lo que b debe ser siempre mayor que 0:
La base del logaritmo es la base de la potencia (color rojo), el exponente de la potencia es el resultado del logaritmo (color verde) y el resultado de la potencia es el contenido del logaritmo (color azul).
Podemos pasar de la forma logarítmica a la forma exponencial según convenga.
Por ejemplo, imagínate que te piden calcular:
No hay ninguna tecla en la calculadora que resuelva los logaritmos en base 2. Por tanto, para calcularlo, debemos pasarlo a su forma exponencial:
Una vez que tenemos la forma exponencial:
Expresamos los dos miembros de la ecuación como potencias de la misma base. En este caso, expresamos ambos miembros como potencias de base 2 (para ello descomponemos el 16 en factores):
Al tener la misma base, directamente obtenemos el valor de x:
Como te he comentado antes, al no tener una tecla en la calculadora que resuelva el logaritmo en base 2.
La tecla «log» de tu calculadora, sirve para resolver logaritmos en base 10. De hecho, cuando no se escribe la base del logaritmo, quiere decir que el logaritmo tiene base 10.
Por ejemplo, este logaritmo:
Que sería equivalente a escribir:
Puedes resolverlo directamente con la calculadora, con la tecla «log». Si lo haces verás que el resultado es 3.
Para comprobar que el procedimiento anterior también funciona, lo voy a resolver así también. Lo paso a su forma exponencial:
Y nos quedamos con esa forma:
Expresamos ambos miembros como potencia de la misma base y directamente obtenemos que el resultado es 3:
Si además de saber cómo resolver logaritmos, quieres aprender a dominar los logaritmos y saber aplicar sus propiedades para resolver ecuaciones logarítmicas, te recomiendo el Curso de Logaritmos.
Ejemplos de cómo resolver logaritmos
Los logaritmos pueden tener diferentes bases y aunque el procedimiento de resolverlos es el mismo, podemos encontrarnos distintas particularidades.
A continuación vamos a resolver 5 ejemplos, para que sepas cómo resolver logaritmos y entiendas mejor cómo aplicar la fórmula de los logaritmos para llegar al resultado.
Ejemplo 1:
Este ejemplo es muy similar al que hemos visto antes.
Pasamos el logaritmo a la forma exponencial. Le hemos añadido una x en el segundo miembro, que es lo que queremos calcular y también para completar la fórmula:
Expresamos ambos términos como potencias de la misma base:
Obtenemos el valor de x:
Por lo que el resultado del logaritmo es:
Ejemplo 2:
Este logaritmo, se diferencia del anterior, en que la base es mayor que el contenido del logaritmo. Pasamos el logaritmo a su forma exponencial:
Esta vez, para expresar ambos miembros como potencias de la misma base, el miembro que transformamos para que ambos miembros tenga la misma base es el primero. El 64 lo factorizamos y lo expresamos como potencia de base 2:
Ahora operamos en el primer miembro, multiplicando los exponentes:
El segundo miembro no tiene exponente, por lo que es equivalente a que tenga un 1. Por tanto, igualamos los exponentes de ambos miembros ahora que tienen la misma base:
Y despejamos la x:
Que es el resultado del logaritmo:
Ejemplo 3:
En este caso, el contenido del logaritmo es una fracción.
Pasamos como siempre el logaritmo a su forma exponencial:
Y ahora hay que convertir la fracción a una potencia con base 2. En primer lugar, el 4 del denominador, lo expresamos en forma de potencia:
Y pasamos la potencia del denominador al numerador, que lo hace con exponente negativo:
Al tenerlo así, ya podemos obtener el valor de x:
Y el resultado del logaritmo es:
Ejemplo 4:
En este caso, tenemos una fracción en la base del logaritmo.
Empezamos igual que siempre, pasando el logaritmo a su forma exponencial:
En este caso, tenemos en el primer miembro escribimos la fracción como potencia, pasando el denominador a numerador, con exponente negativo y en el segundo miembro lo factorizamos para expresarlo también en forma de potencia:
Operamos en el primer miembro, multiplicando exponentes:
Y al tener la misma base, ya podemos igualar los exponentes, de donde obtenemos el valor de x:
Que es el resultado del logaritmo:
Ejemplo 5:
En este último ejemplo, el contenido del logaritmo es un número decimal.
Como siempre, pasamos el logaritmo a su forma exponencial:
Escribimos el número decimal en forma de fracción:
Simplificamos la fracción:
Y ahora vemos que la fracción resultante la podemos escribir en forma de potencia de base 2, tal y como hicimos en el ejemplo 3:
Por lo que x será:
Que es igual al valor del logaritmo:
Con estos cinco ejemplos ya sabes cómo resolver logaritmos de distintas bases y expresados de distintas formas
Qué es un logaritmo neperiano
Una vez que tenemos claro qué es un logaritmo y cómo se resuelve, vamos a ver qué es un logaritmo neperiano.
Se llama logaritmo neperiano, escrito como ln, al logaritmo que tiene como base el número e (logaritmo en base e), que aplicando la fórmula de los logaritmos sería:
Logaritmo en base e no se escribe nunca (sólo lo he puesto para que entiendas mejor la fórmula). Directamente, el logaritmo en base 3, se escribe como logaritmo neperiano, ln:
Por tanto, la fórmula con ln quedaría:
Con los logaritmos neperianos no tenemos el problema de tener distintas bases, ya que siempre son de base e, por lo que podemos resolverlos directamente con la calculadora, gracias a la tecla «ln».
Sin embargo, si el contenido del logaritmo neperiano está expresado con el número e, podemos resolverlos de forma manual siguiendo el procedimiento habitual.
Por ejemplo:
Pasamos el ln a su forma exponencial. En su forma exponencial, el ln siempre tiene el número e elevado a x en el primer miembro. El segundo miembro es el contenido del ln:
De donde obtenemos que:
Vamos a ver otro ejemplo:
En este caso, el número e está en el denominador de una fracción. Al pasar el ln a su forma exponecial nos queda:
Pasamos el número e al numerador con exponente negativo:
Y el valor de x será:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: