A continuación voy a explicarte qué es la afinidad y cómo obtener puntos, rectas y figuras afines. Veremos lo necesario para aplicarlo después en ejercicios de sistema diédrico, por lo que no se trata de estudiar la afinidad a fondo.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Qué es la afinidad
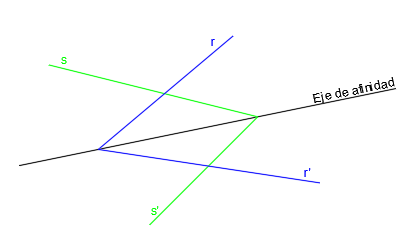
La afinidad es una transformación geométrica en la que a cada punto se le asocia otro punto (punto afín), a cada recta se le asocia otra recta (recta afín) y en general, a una figura plana se le asocia otra figura plana (figura afín).
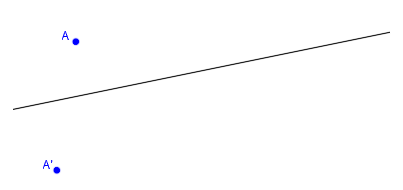
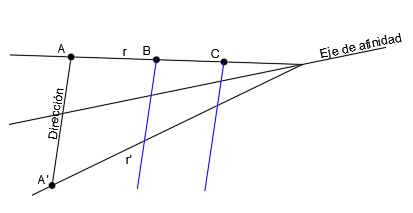
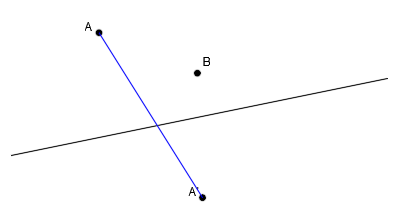
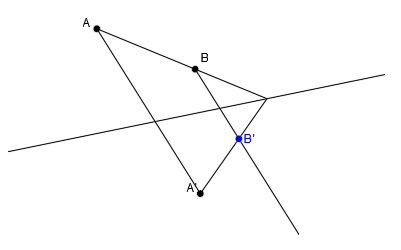
Por ejemplo, al punto A le corresponde el punto A’:
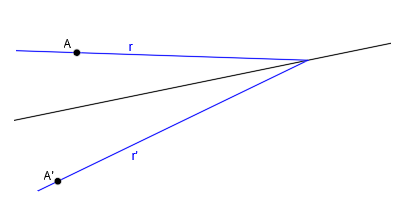
Y la recta r tiene asociada la recta r’:
Se compone de los siguientes elementos:
- El eje de afinidad
- La dirección de afinidad
Vamos a ver cada uno de ellos más despacio.
Eje de afinidad
El eje de afinidad es el eje a partir del cual se obtienen los elementos afines (parecido a un eje de simetría, para que me entiendas, pero con algunas diferencias que verás más abajo).
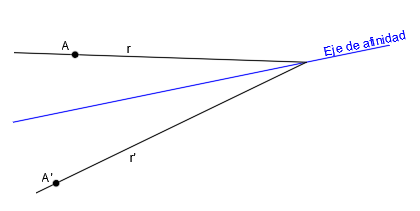
En las figuras anteriores, este es el eje de simetría:
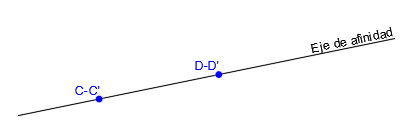
Es una recta compuesta por puntos que son afines de sí mismos, es decir, que un punto que pertenezca al eje de simetría coincide con su punto afín. Son puntos dobles:
Además, es el lugar geométrico donde se cortan todas las rectas afines, es decir, las rectas cotan con sus rectas afines en el eje de afinidad:
Esto se debe a que para dibujar una recta, necesitamos al menos dos puntos para unirlos y si uno de los puntos se encuentra en el eje de afinidad, al ser un punto doble, pertenece a la recta como a su recta afín.
Dirección de afinidad
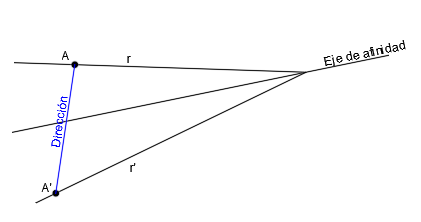
La dirección de afinidad es la que define dos puntos afines, es decir, si unimos un punto con su punto afín, obtendremos una recta que será paralela a la dirección de afinidad.
Todos los puntos tendrán la dirección de afinidad paralela, así que, una vez conocida la dirección de afinidad, podemos dibujar puntos afines pertenecientes a una misma recta.
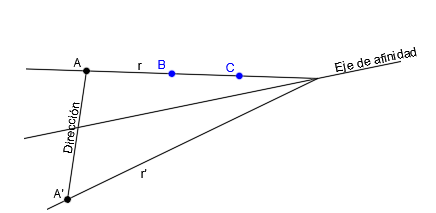
Por ejemplo, vamos a tomar los puntos B y C de la recta r:
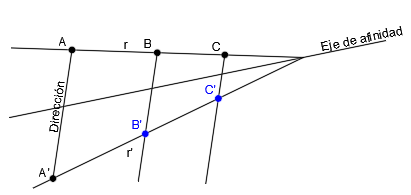
Para dibujar sus puntos afines, a partir de cada punto, trazamos su dirección, que es paralela a la dirección de A-A’:
Donde las direcciones corten con la recta afín r’, tendremos los puntos afines B’ y C’:
Date cuenta, que para dibujar un punto afín, además de la dirección, necesitamos una recta (lo veremos con más detalle más abajo).
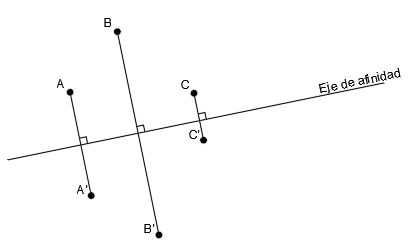
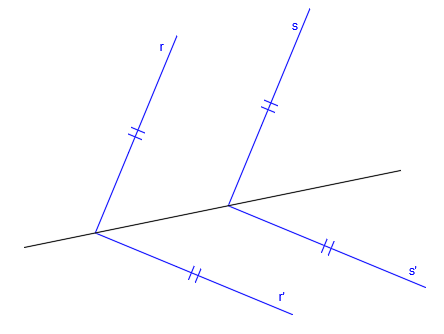
Si la dirección de afinidad es perpendicular al eje de afinidad, entonces se trata de una afinidad ortogonal:
En el resto de casos, se llamara afinidad oblicua.
Cómo obtener puntos afines
Vamos a ver ahora cómo obtener nuevos punto afines paso por paso.
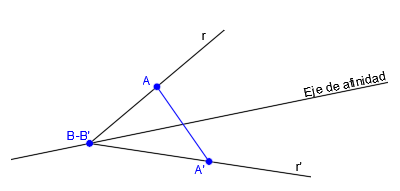
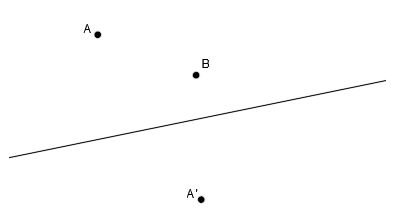
Necesitaremos como mínimo, un punto y su punto afín (puntos A y A’), el eje de afinidad y el punto al que queremos obtener su afín (punto B):
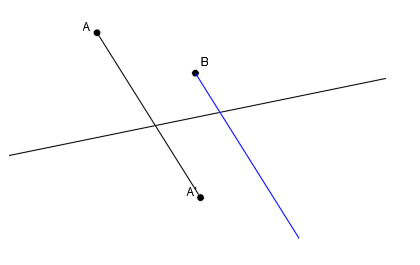
Lo primero que tenemos que sabes es la dirección de afinidad, así que, para ello, unimos el punto A con su punto afín A’:
Ya sabemos la dirección de afinidad que tendrá cualquier punto. Ahora desde el punto B, trazamos su dirección, que será paralela a la dirección A-A’:
El punto afín B’ se encontrará en un punto de su dirección, pero ¿cómo sabemos ese punto?
Para saber en qué punto de la dirección de B estará su afín B’, necesitamos apoyarnos en una recta y su recta afín. El punto B’, se encontrará en el punto de corte de la recta afín y la dirección.
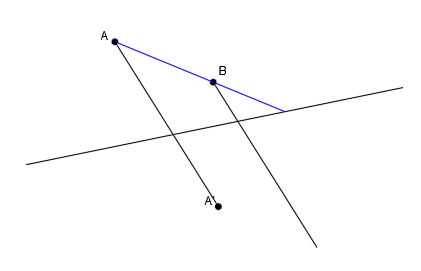
Así que dibujamos una recta que pase por los puntos A y B y llegue hasta el eje de afinidad:
Ahora dibujamos su recta afín sabiendo que parte desde el mismo punto de corte del eje de afinidad y para por el punto afín A’:
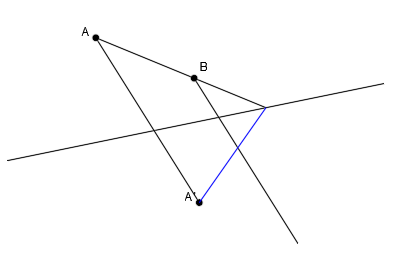
En el punto donde se cortan la recta afín y la dirección del punto B, será el punto afín B’:
Para hallar el punto afín a un punto, siempre necesitaremos la recta afín por la que pasa para tener el punto de corte con su dirección.
Propiedades de las rectas en la afinidad
Vamos a ver algunas propiedades de las rectas en la afinidad que nos ayudarán mucho a la hora de resolver ejercicios.
Rectas afines a rectas paralelas
Si dos rectas son paralelas, sus rectas afines también serán paralelas:
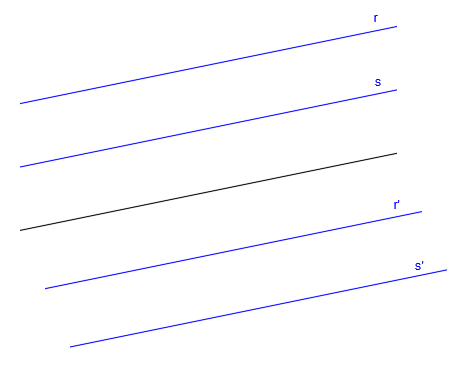
Rectas paralelas al eje de afinidad
Las rectas paralelas al eje de afinidad tienen rectas afines que también serán paralelas al eje de afinidad:
Ejercicio resuelto de afinidad
Vamos a resolver un ejercicio de afinidad, que aplicaremos en ejercicios de sistema diédrico.
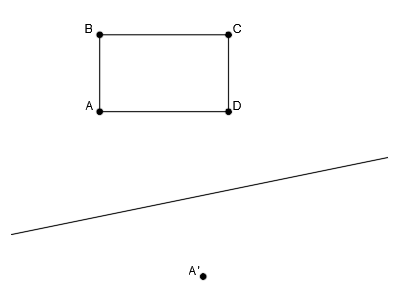
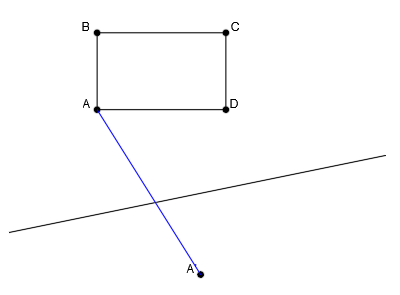
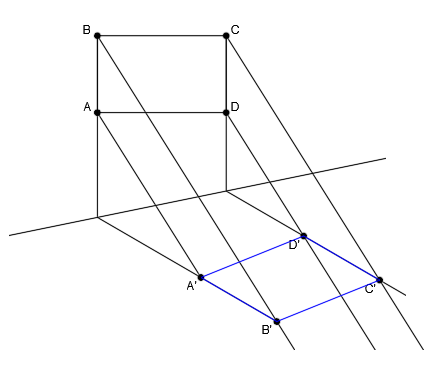
Tenemos que hallar la figura afín a la figura dada:
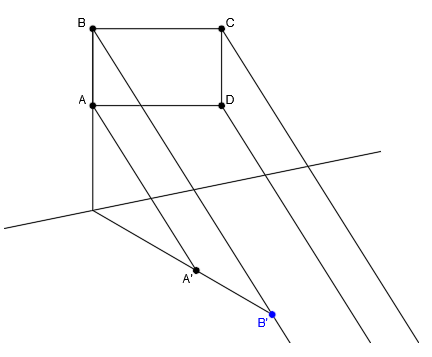
Tenemos una figura definida por los puntos A, B, C y D, el eje de afinidad y el punto afín A’.
La figura afín a la figura dada se obtiene hallando los puntos afines de cada punto y después uniendo los puntos afines. Vamos a verlo paso a paso.
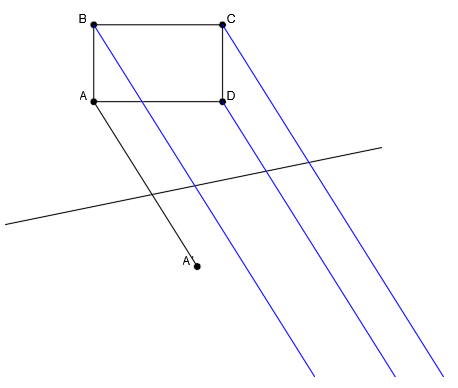
Primero unimos el punto A con su afín A’, para determinar la dirección de afinidad:
Trazamos la dirección del resto de puntos sabiendo que será paralelas entre sí:
Ahora necesitamos saber en qué punto de su dirección se encuentra cada punto afín, por lo que necesitamos trazar rectas y sus rectas afines para encontrar los distintos puntos de corte con las distintas direcciones.
Como sólo tenemos el afín del punto A, sólo podemos dibujar rectas que pasen por el punto A, para después poder dibujar su recta afín.
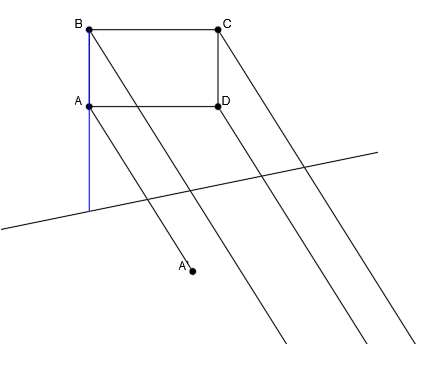
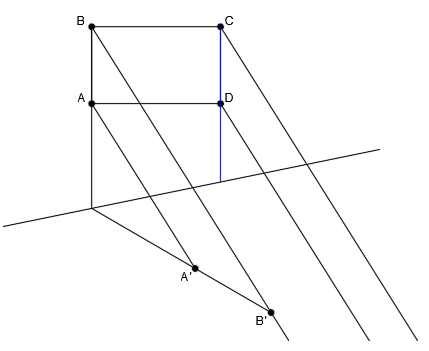
El punto B se encuentra en la misma recta que el punto A. Por tanto, trazamos una recta que pase por los puntos A y B:
Dibujamos su recta afín partiendo del punto de corte con el eje de afinidad y pasando por el punto afín A’:
El punto de corte de esta recta afín con la dirección de B será el punto afín B’:
Como A y B se encuentran en la misma recta, sus puntos afines A’ y B’ también se encontrarán en la misma recta.
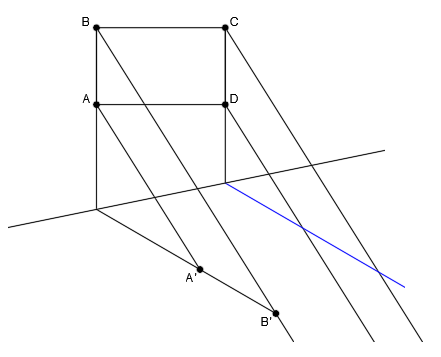
Vamos a apoyarnos en la propiedad de las rectas paralelas en la afinidad. La recta que pasa por los puntos C y D es paralela a la recta A-B:
Así que, su recta afín será paralela a la recta A’-B’, partiendo desde el punto de corte con el eje:
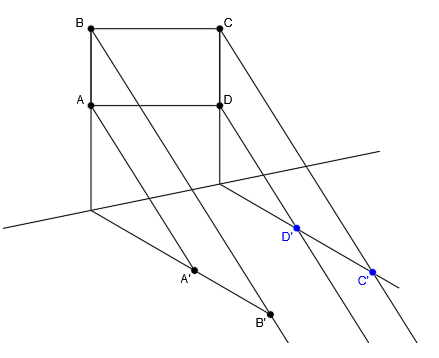
El punto de corte de esta recta afín con las direcciones de C y D serán los puntos afines C’ y D’:
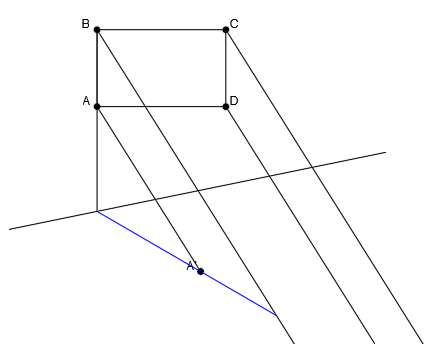
Por último, unimos los puntos afines tal y como se encuentran los puntos originales. Unimos A’ con B’, B’ con C’, C’ con D’ y D’ con A’:
Y ya tenemos la figura afín a la figura original.
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE