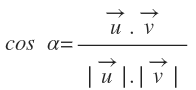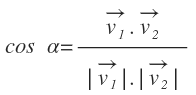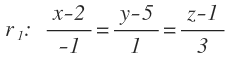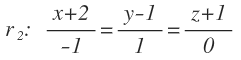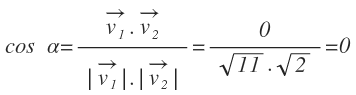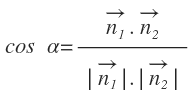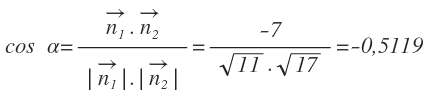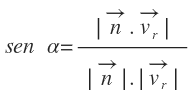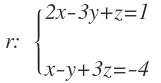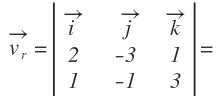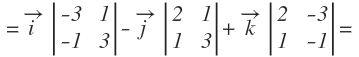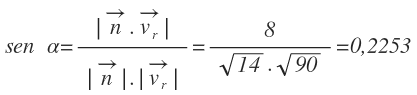A continuación te voy a explicar cómo obtener el ángulo que forman rectas y planos en el espacio, como el ángulo entre dos rectas, el ángulo entre dos planos y el ángulo entre recta y plano. Con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Antes de empezar, hay que indicar que si sabemos que si tenemos dos vectores:
Podemos obtener el ángulo que forman tan solo despejando el coseno del ángulo en la expresión del producto escalar:
Ya que conocidas las coordenadas de los vectores, podemos calcular su módulo y su producto escalar mediante la expresión analítica:
Por tanto, el hecho de saber calcular el ángulo de dos vectores, nos va a permitir calcular los ángulos entre los elementos del espacio.
Cómo calcular el ángulo de dos rectas en el espacio
El ángulo que forman dos rectas que se cortan en el espacio es el menor de los ángulos que forman sus respectivos vectores de dirección.
Por tanto, para calcular el ángulo entre dos rectas en el espacio, debemos calcular el ángulo entre sus vectores de dirección despejando el coseno del ángulo de la fórmula del producto escalar de esos dos vectores:
Ejercicio resuelto
Calcular el ángulo formado por las siguientes rectas:
Debemos obtener el vector de dirección de cada recta, que lo tienes explicado en la lección donde explico las ecuaciones de la recta en el espacio.
El vector de dirección de la primera recta es:
Y el vector de dirección de la segunda recta es:
Una vez tenemos los dos vectores, el coseno del ángulo viene dado por la fórmula:
El producto escalar lo calculamos mediante su expresión analítica:
Por otro lado, calculamos los módulos de cada vector. El módulo del primer vector es:
El módulo del segundo vector es:
Sustituimos en la fórmula:
Y por último, para obtener el ángulo, hacemos la inversa del coseno:
En este caso, las rectas forman un ángulo de 90º, es decir, son perpendiculares.
Cómo calcular el ángulo de dos planos
El ángulo que forman dos planos en el espacio es el menor de los ángulos que forman sus respectivos vectores normales.
Por tanto, para calcular el ángulo entre dos planos en el espacio, debemos calcular el ángulo entre sus vectores normales despejando el coseno del ángulo de la fórmula del producto escalar de esos dos vectores:
Ejercicio resuelto
Calcular el ángulo formado por los siguientes planos:
En primer lugar, debemos obtener el vector normal de cada plano, que lo tienes explicado en la lección donde explico las ecuaciones del plano.
El vector normal del primer plano es:
El vector normal del segundo plano es:
El coseno del ángulo que forman esos dos vectores viene dador por al siguiente fórmula:
El producto escalar de los dos vectores normales lo hallamos mediante la expresión analítica del producto escalar:
Calculamos el módulo de cada uno de los vectores normales. El módulo del primer vector es:
El módulo del segundo vector es:
Sustituimos los valores en la fórmula del coseno del ángulo:
Y hallamos el ángulo con la inversa del coseno:
Por definición, el ángulo que forman los dos planos es el menor de los ángulos que forman sus vectores normales, los cuales son suplementarios. Por tanto, el ángulo calculado no es el menor y para hallar el ángulo que forman los planos hay que calcular el ángulo suplementario al que acabamos de calcular:
Los planos están formando un ángulo de 59,2º.
Cómo calcular el ángulo entre una recta y un plano en el espacio
El ángulo entre una recta y un plano en el espacio es el ángulo complementario del menor ángulo que forman el vector de dirección de la recta y el vector normal del plano.
En este caso, el seno del ángulo que forman los dos vectores se calcula a través de la siguiente expresión:
Date cuenta, de que esta vez estamos calculando el seno y no el coseno y que el producto escalar del numerador de la fracción está en valor absoluto. Esto es así para que nos dé directamente el valor del ángulo que buscamos y no tengamos que estar calculando después el ángulo complementario.
Ejercicio resuelto
Calcular el ángulo formado por el siguiente plano y la siguiente recta:
El vector normal al plano es:
La recta está expresada en sus ecuaciones implícitas, es decir, las ecuaciones de dos planos. En este caso, el vector de dirección se calcula como el producto vectorial de los vectores normales de cada plano:
Por tanto, el vector de dirección de la recta es:
Ya tenemos los dos vectores que necesitamos. Ahora vamos a calcular el seno del ángulo que forman mediante la fórmula:
Por un lado calculamos el producto escalar con ayuda de la expresión analítica:
Por otro lado, calculamos los módulos de cada vector. El módulo del vector normal del plano es:
El módulo del vector de dirección de la recta es:
Sustituimos los valores en la fórmula y calculamos el valor del seno del ángulo que forman:
Finalmente, para obtener el ángulo, realizamos la inversa del seno:
El plano y la recta están formando un ángulo de 13,02º.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: