A continuación te voy a explicar todo lo que debes saber sobre los ángulos: qué son, cómo se miden los ángulos y todos los tipos de ángulos que existen, para que puedas entender por ejemplo cómo calcular el ángulo que forman las agujas de un reloj, así cómo todos los demás cálculos relacionados con ángulos.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es un ángulo
Un ángulo es la parte del plano limitada por dos semirrectas que parten de un mismo punto. Las semirrectas que forman el ángulo se llaman lados y el punto donde se encuentran es el vértice:
Se suelen nombrar con una letra mayúscula en el vértice (A, B, C …) o mediante letras griegas (α, β, γ …).
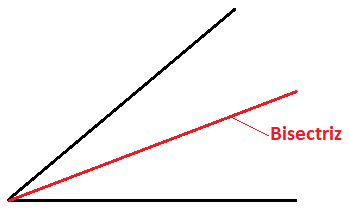
Bisectriz de un ángulo
La bisectriz de un ángulo es la semirrecta que divide al ángulo en dos partes iguales, pasando por el centro. También se puede definir como el lugar geométrico cuyos puntos están a la misma distancia de los lados del ángulo:
Cómo se miden los ángulos
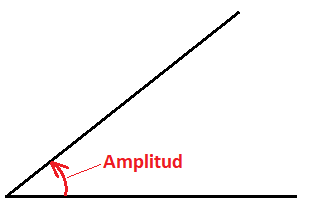
Los ángulos, al no ser figuras cerradas, no se puede medir su área ni su perímetro. Por tanto, cuando hablamos de medida de ángulos nos referimos a su amplitud.
La amplitud de un ángulo es la extensión de plano que ha de recorrer uno de los lados hasta alcanzar la posición del otro, cuando se le hace girar alrededor del vértice:
Por otro lado, la amplitud de un ángulo no depende de la longitud de sus lados. Por ejemplo, en estos dos ángulos, aunque la longitud de sus lados es distinta, la amplitud es la misma:
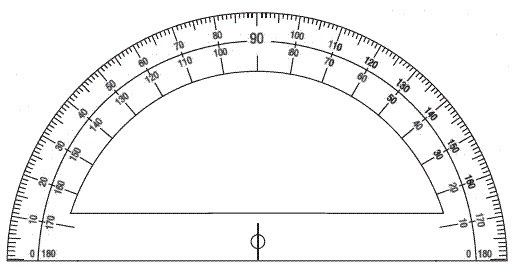
Para medir los ángulos se utiliza un semicírculo graduado llamado transportador de ángulos:
En general, los transportadores de ángulos suelen tener dos escalas, una interior y otra exterior, para medir los ángulos en función de su orientación.
Para medir ángulos con el transportador, se coloca el transportador de manera que uno de los lados del ángulo coincida con la línea horizontal del transportador y el vértice del ángulo coincida con el centro del semicírculo, marcado con una línea vertical. El otro lado del ángulo indicará sobre la graduación del transportador los grados de amplitud del ángulo.
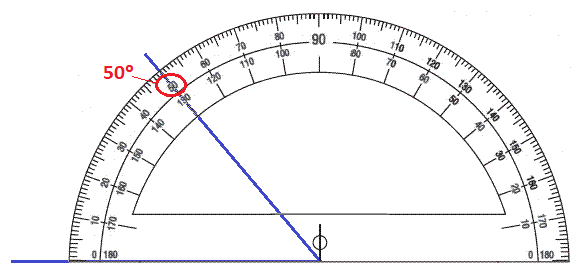
Por ejemplo, en este caso, el ángulo tiene una amplitud de 50º:
Como el ángulo está orientado hacia la derecha, hemos utilizado la escala interior, que es la que empieza en 0º para esa orientación. Si el ángulo estuviera orientado hacia la izquierda, hubiéramos utilizado la escala exterior:
Comúnmente, los ángulos se pueden medir en grados sexagesimales (según el sistema sexagesimal), donde un grado equivale a 60 minutos.
También se pueden medir en grados centesimales, aunque es menos frecuente, donde un grado equivale a 100 minutos.
Tipos de ángulos
Vamos a ver todas las clases de ángulos que existen:
Ángulo agudo
Un ángulo agudo es el que tiene una amplitud menor de 90º:
Ángulo recto
Un ángulo recto es el que tiene una amplitud igual a 90º:
Ángulo obtuso
Un ángulo obtuso es aquel que tiene una amplitud mayor de 90º, pero menor de 180º:
Ángulo llano
Un ángulo llano es el que tiene una amplitud igual a 180º:
Ángulo convexo
Se llama ángulo convexo a todos los ángulos que sean menores de 180º. Todos los ángulos anteriores, a excepción del ángulo llano, son ángulos convexos.
Ángulo cóncavo
Un ángulo cóncavo es aquel que es mayor de 180º pero menor de 360º:
Ángulo completo
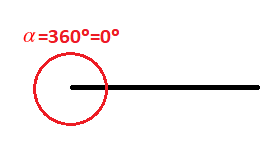
Un ángulo completo es aquel cuyos dos lados coinciden. Su amplitud es de 360º, o de 0º que es lo mismo:
Ángulos iguales
Los ángulos iguales son aquellos que tienen la misma amplitud, es decir, que tienen el mismo número de grados:
Ángulos complementarios
Los ángulos complementarios son aquellos que al sumarlos, el resultado es un ángulo recto, es decir, 90º:
Ángulos suplementarios
Los ángulos suplementarios son los que forman un ángulo llano, es decir, 180º, al sumarlos:
Ángulos adyacentes
Los ángulos adyacentes son ángulos que tienen un vértice y un lado en común. Los ángulos adyacentes suman siempre 180º:
Ángulos consecutivos
Los ángulos consecutivos son aquellos que están colocados uno a continuación de otro, coincidiendo en una de las semirrectas:
Ángulos opuestos por el vértice
Los ángulos opuestos por el vértice son ángulos que tienen el vértice en común y cada uno de sus lados pertenece a la misma semirrecta. Los ángulos opuestos por el vértice son iguales:
Ángulos formados por una recta que corta a dos paralelas
Cuando una recta corta a otras dos rectas paralelas, se forman 8 ángulos:
Estos 8 ángulos guardan la siguiente relación entre ellos:
- Los ángulos correspondientes son iguales:
- 1 es igual a 5
- 2 es igual a 6
- 3 es igual a 7
- 4 es igual a 8
- Los ángulos externos son iguales:
- 1 es igual a 8
- 2 es igual a 7
- Los ángulos internos son iguales:
- 3 es igual a 6
- 4 es igual a 5
- Los ángulos opuestos por el vértice son iguales:
- 1 es igual a 4
- 2 es igual a 3
- 5 es igual a 8
- 6 es igual a 7
- Los ángulos conjugados externos 1 y 7, 2 y 8 son suplementarios
- Los ángulos internos 3 y 5, 4 y 6 son suplementarios
Con la ayuda de estos ángulos es posible determinar el valor de ciertos ángulos en los problemas de geometría.
Ángulo diedro
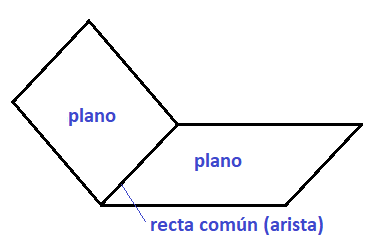
El ángulo diedro es la porción de espacio comprendido entre dos planos que tienen la misma recta de origen:
Ángulo poliedro
El ángulo poliedro es la porción de espacio formada por la intersección de tres o más planos que se cortan en un punto:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: