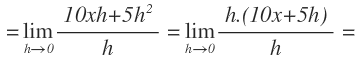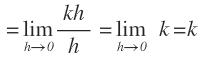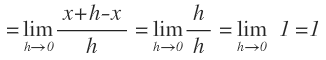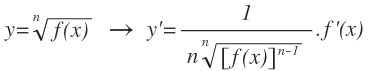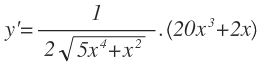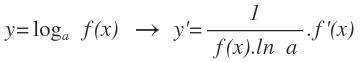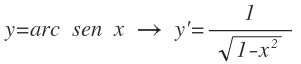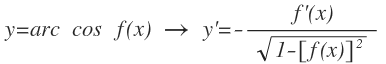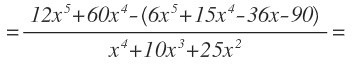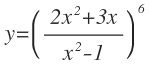En esta lección te voy a explicar qué es la función derivada, cómo obtener las funciones derivadas para cada uno de los tipos de funciones y cómo utilizar las fórmulas de estas funciones para derivar.
Veremos también las operaciones con funciones derivadas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Tienes disponibles el Curso de Derivadas donde te explico con todo detalle cómo derivar todo tipo de funciones.
Función derivada
Hasta ahora, para calcular la derivada de una función en un punto lo hemos hecho utilizando la definición de la derivada:
Utilizando la definición de derivada, podemos obtener la función derivada de una función, es decir, una función que asocia a cada punto con la derivada en dicho punto.
Es decir, en vez de calcular la derivada para un sólo punto, la podemos calcular para x:
El resultado será una función que depende de x y para obtener la derivada en un punto en concreto, sólo tenemos que sustituir la x por ese punto en la función derivada.
No hay que confundir los conceptos de derivada de una función en un punto, que es un número real, con una función derivada o simplemente derivada, que es una función.
Vamos a ver un ejemplo: Hallar la función derivada de la siguiente función:
Aplicamos la definición de derivada:
Sustituimos f(x+h) y f(x) por sus funciones correspondientes:
Operamos y simplificamos términos:
Anulamos la h del numerador y del denominador y por último obtenemos el resultado:
Por tanto, la función derivada de la función anterior es:
Esta vez, la función derivada es una función constante, es decir, no es el valor de la derivada en un punto, lo que quiere decir que la derivada de la función anterior en cualquier punto es igual a 7.
Si calculamos el valor de la función derivada en cualquier punto, el resultado siempre será 7:
Vamos a ver otro ejemplo.
Hallar la función derivada de la siguiente función:
y halla el valor de la derivada de esa función en el punto x=2.
En primer lugar aplicamos la fórmula de la definición de derivada:
Sustituimos f(x+h) y f(x) por sus valores:
Desarrollamos el paréntesis que está al cuadrado:
Eliminamos paréntesis:
Simplificamos términos y sacamos factor común a la h en el numerador:
Eliminamos la h que se repite en el numerador y en el denominador y obtenemos el resultado final:
La derivada de la función es por tanto:
Para hallar el valor de la derivada en x=2, ya no es necesario aplicar la fórmula de la derivada. Simplemente sustituyendo la x por 2 en la función derivada, obtenemos su valor para ese punto:
Cálculo de funciones derivadas
Si conocemos la función derivada de cada tipo de función, podemos escribirla directamente sin necesidad de calcular cada vez la función derivada utilizando su definición.
Esto nos permite calcular derivadas de una forma más directa, al mismo tiempo que simplifica mucho los cálculos en funciones más complejas.
Vamos a ver a continuación como es la derivada de cada uno de los tipos de funciones:
Derivada de una constante
Tenemos una función constante:
La derivada de una función constante es cero:
Vamos a demostrarlo calculando su función derivada utilizando la definición:
Por tanto, cada vez que la función sea una constante, la derivada será 0 y lo puedes poner directamente.
Por ejemplo: Calcular la derivada de la siguiente función:
Como es una función constante, escribimos directamente su derivada:
Derivada de la función lineal
Las funciones lineales son aquellas cuya forma son una x multiplicadas por un número:
La derivada de la función lineal es el número que multiplica a la x:
Su demostración es la siguiente:
Por tanto, cuando las función sea lineal, en su derivada desaparecerá la x y se quedará sólo el número:
Vamos a ver un ejemplo: Calcular al derivada de la siguiente función:
Su derivada es igual al número que tiene delante la x:
Derivada de la identidad
Un caso particular de la función lineal es la función identidad, es decir, cuando la función es sólo una x::
La derivada de la función identidad es igual a 1, que es igual al número que lleva delante:
Su demostración es:
Derivada de la función afín
La función afín es la que tiene la siguiente forma:
La derivada de la función afín es el número que queda delante de la x. Todo lo demás desaparece:
Tiene sentido ya que la derivada de una función linea es el número que queda delante de la x y la derivada de un una constante es cero, por tanto, la suma de las dos derivadas es igual al número que queda delante de la x.
Veremos más adelante que la derivada de una suma de funciones es igual a la suma de las derivadas.
Su demostración derivando con la definición de la derivada es:
Por ejemplo, calcular la derivada de:
Directamente para calcular la derivada de esta función, dejamos sólo el número que está multiplicando a la x:
Derivada de la función potencial
Una función potencial es aquella donde la x está elevada a un exponente. Para calcular su derivada, el exponente pasa a multiplicar a la x y se le resta 1 al exponente:
En lugar de una x, podemos tener una función elevada a un exponente. En ese caso, la derivada se calcula pasando el exponente a multiplicar a la función, a cuyo exponente se le resta 1 y además todo lo anterior queda multiplicado por la derivada de la función:
Por ejemplo, calcular la derivada de:
Pasamos el 2 multiplicando a la x y le restamos 1 al exponente:
Vamos a ver otro ejemplo con una función elevada a un exponente: Derivar la siguiente función:
Pasamos el exponente a multiplicar la función y al exponente de la función le restamos 1 y todo eso, lo multiplicamos por la derivada de la función, que esta compuesta por dos términos y su derivada será la suma de la derivada de cada uno de los términos:
En este vídeo tienes ejercicios explicados paso a paso sobre cómo derivar funciones potenciales:
Derivada de una constante por una función
Cuando tenemos una constante que está multiplicando a una función, su derivada será esa constante multiplicada por al derivada de la función:
Por ejemplo:
El 3 lo pasamos multiplicando y queda multiplicando al 27, que ya estaba. Al exponente de la x le restamos 1:
Derivada de una raíz
La derivada de una raíz es un caso particular de la función potencial cuando el exponente es fraccionario. La derivada de la raíz cuadrada de x es la siguiente:
Si lo que tenemos es una función dentro de la raíz cuadrada, su derivada es:
En general, la derivada de una raíz, ya sea de x o de una función es:
Por ejemplo:
En el denominador, el índice pasa a multiplicar a la raíz y se le resta 1 al exponente del radicando:
Vamos a ver otro ejemplo de calcular la derivada de la raíz cuadrada de una función:
Derivada del logaritmo
La derivada de un logaritmo de x de base cualquiera es igual a 1 dividido por el producto de x por el logaritmo neperiano de la base:
Cuando el logaritmo es de una función, su derivada es igual a 1 entre el producto de la función por el logaritmo neperiano de la base, multiplicado por la derivada de la función:
Cuando la función es logaritmo neperiano de x, su derivada es 1 entre x:
Y si la función es logaritmo neperiano de una función, su derivada es 1 entre la función, multiplicado por la derivada de la función:
Por ejemplo, la derivada de este logaritmo en base 12 de esta función es:
En este vídeo tienes ejercicios resueltos de cómo derivar funciones logarítmicas paso a paso:
Derivada de la función exponencial
Tenemos una función exponencial cuando la x está en el exponente. Su derivada es igual al mismo número elevado a x multiplicado por el logaritmo neperiano de la base de la potencia:
Si el número está elevado a una función, la derivada es igual a la misma potencia, multiplicada por el logaritmo neperiano de la base y por al derivada de la función exponente:
Cuando el número al que está elevado la x es el número e, la derivada es el mismo número e elevado a x:
Si el número e está elevado a una función, su derivada es el mismo número e elevado a la función por la derivada de la función:
Por ejemplo, en esta función exponencial, donde el número está elevado a una función:
Su derivada es:
En este otro ejemplo con el número e elevada a una función:
Su derivada es:
Aquí tienes un vídeo donde explico paso a paso cómo derivar funciones exponenciales con ejercicios resueltos:
Derivada de las funciones trigonométricas
Vamos a ver ahora las derivadas de las funciones trigonométricas junto con sus funciones compuestas.
La derivada del seno es igual al coseno:
La derivada del coseno, es igual a menos seno:
La derivada de la tangente es igual a 1 más el cuadrado de la tangente o 1 entre el coseno cuadrado de x:
Esas tres funciones trigonométricas son las más utilizadas. Te dejo también el resto de funciones trigonométrica:
Contangente:
Secante:
Cosencante:
Veamos algunos ejemplos sobre derivar funciones trigonométrica.
Derivar la siguiente función seno:
Derivar la siguiente función coseno:
Derivar la siguiente función tangente:
Derivar la siguiente función cotangente:
Aquí tienes un vídeo de cómo derivar funciones trigonométricas con ejercicios resueltos paso a paso:
Derivada de las funciones trigonométricas inversas
Éstas son las derivadas de las funciones trigonométricas inversas principales.
Arco seno:
Arco coseno:
Arco tangente:
Operaciones con funciones derivadas
Vamos a ver ahora cómo derivar funciones que están formadas por más de una función, como la suma, la multiplicación, el cociente o la composición de funciones.
La derivada de la suma de dos funciones ya la hemos comentado un poco en el apartado anterior.
Derivada de la suma de dos funciones
La derivada de una suma de dos funciones es igual a la suma de las derivadas de esas dos funciones:
Por ejemplo, la derivada de la siguiente función:
es igual a la derivada de cada uno de sus términos:
Derivada de un producto de funciones
La derivada del producto de dos funciones es igual a la derivada de al primera función, por la segunda sin derivar, más la primera sin derivar, por la derivada de la segunda:
Por ejemplo:
Derivada del cociente de funciones
La derivada de un cociente de funciones es igual a la derivada del numerador, por el denominador sin derivar, menos el numerador sin derivar por la derivada del denominador, todo ello dividido entre el denominador sin derivar al cuadrado:
Por ejemplo:
Una vez aplicada la fórmula de la derivada de un cociente, ya sólo queda operar y agrupar términos semejantes:
Regla de la cadena. Derivada de la función compuesta
En las funciones compuestas por otras funciones:
Su derivada se calcula aplicando la regla de la cadena, que consiste en ir derivando la función que queda por fuera, multiplicada por la derivada de la función de dentro:
Por ejemplo, esta función se compone de una función elevada a 4:
La función de fuera es la función elevada a 4 y al función de dentro corresponde a un polinomio.
Por tanto, aplicamos la regla de la cadena derivando la función que queda por fuera, es decir, la función elevada a 4, que pasamos el 4 a multiplicar y le restamos uno al exponente, y lo multiplicamos por la derivada de la función de dentro, que corresponde a la suma de sus derivadas:
Veamos otro ejemplo. En este caso, tenemos una función compuesta por una función elevada a 6:
La función que queda por fuera es una función elevada a 6 y la función de dentro es un cociente de funciones:
La regla de la cadena la hemos ido aplicando en el cálculo de cada una de las funciones derivadas compuestas, es decir, cuando estaban formadas por una función, ya que si te das cuenta, todas están multiplicadas por f'(x).
Tabla de derivadas
Te dejo aquí una recopilación de todas las derivadas para que lo tengas todo más a mano:
>> Descargar tabla de derivadas pdf
¿Quieres aprender a derivar desde cero? Pues te recomiendo el Curso de Derivadas, en el que te enseñaré paso a paso a derivar todo tipo de funciones, con ejercicios resueltos paso a paso y ejercicios propuestos para que practiques. Además me puedes preguntar todas tus dudas.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: