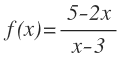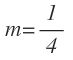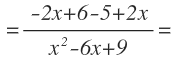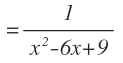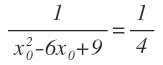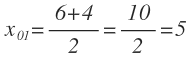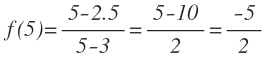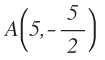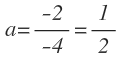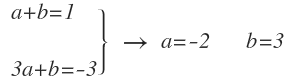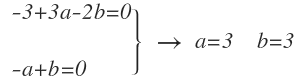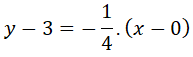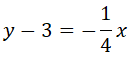En esta lección te voy a explicar todo lo necesario para calcular la ecuación de la recta tangente a una curva definida por una función.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo calcular la recta tangente a una curva en un punto
Para calcular la ecuación de la recta tangente, utilizaremos la ecuación punto-pendiente:
Por lo que necesitamos saber las coordenadas de un punto P que pase por la recta, que será el punto donde la recta es tangente a la curva y además, la pendiente de esa recta:
Para calcular las coordenadas del punto donde la recta es tangente, si nos dan la coordenada x del punto, sólo tenemos que sustituir la x por la coordenada en la función y obtendremos la coordenada «y», ya que la coordenada y coincide con el valor de la función para ese valor de x.
Por otro lado, la pendiente de la recta tangente a un punto de una función coincide con el valor de la derivada de la función en ese punto:
Por lo que derivando la función de la curva y sustituyendo por el valor de x del punto donde es tangente la curva, obtendremos el valor de la pendiente m.
Si conocemos la pendiente m, pero no conocemos las coordenadas del punto donde la recta es tangente a la curva, se puede despejar la x a partir de la fórmula anterior.
Otras veces nos piden que la recta tangente debes ser paralela a otra recta dada. Dos rectas paralelas tienen la misma pendiente, por lo que a partir de la recta dada, podemos obtener la pendiente.
Para que quede más claro, vamos a ver cada uno de estos casos con varios ejercicios resueltos.
Ejercicios resueltos de cálculo de la recta tangente a una curva
En este vídeo te dejo los dos primeros ejercicios sobre el cálculo de la recta tangente a una curva:
Y aquí los tienes en formato texto:
Ejercicio 1
Hallar la ecuación de la recta tangente a la curva:
en el punto x=-1.
Como he comentado antes, para el cálculo de la ecuación de la recta tangente, utilizaremos la ecuación punto-pendiente:
Necesitamos obtener las coordenadas del punto P,que será el punto donde la recta es tangente a la curva y la pendiente de la recta tangente:
Vamos a calcular las coordenadas del punto P. Ya tenemos la coordenada x, ya que nos la da el enunciado. Para calcular la coordenada «y» sólo tenemos que sustituir la x por -1 en la función y operar:
La coordenada «y» es y=3.
Por tanto, las coordenadas del punto P, donde la recta es tangente es:
Ahora vamos a calcular la pendiente de la recta tangente, que será igual a la derivada de la función en el punto P, es decir, cuando x=-1:
Por tanto, calculamos la derivada de la función:
Si necesitas aprender a derivar o reforzar conceptos, te recomiendo el Curso de Derivadas, en el que aprenderás a derivar, paso a paso, desde el principio.
Obtenemos el valor de la derivada de la función para x=-1:
La pendiente de la recta es igual a 2.
Ya tenemos lo que necesitamos para calcular la ecuación de la recta:
Por tanto, en la ecuación punto-pendiente:
Sustituimos las coordenadas del punto y la pendiente por sus valores:
Y operamos:
Llegando a la ecuación de la recta tangente que estábamos buscando.
Vamos con otro ejercicio un poco diferente.
Ejercicio 2
Hallar la ecuación de la recta tangente a la curva:
para que dicha tangente sea paralela a la recta de ecuación:
En este caso no sabemos ninguna coordenada del punto donde la recta es tangente a la curva, pero nos dan el dato de que debe ser paralela a otra recta, por lo que indirectamente nos están dando la pendiente.
Igual que antes, la ecuación de la recta tangente la obtendremos a partir de la ecuación punto-pendiente:
Por lo que necesitamos saber las coordenadas del punto y la pendiente:
La pendiente la obtenemos a partir de la recta que nos da el enunciado. Vamos a calcular la pendiente de esa recta. Para ello despejamos la «y» y el número que quede delante de la x, será la pendiente:
La pendiente de la recta que nos da el enunciado es -3, y como nos dice que es paralela a la recta tangente, la pendiente de la recta tangente también es -3:
Ahora vamos a calcular las coordenadas del punto P.
Sabemos que la pendiente en cualquier punto de la curva es igual al valor de la derivada en ese punto:
Como ya sabemos la pendiente, sólo nos queda calcular la pendiente y obtendremos la coordenada x que cumple que la pendiente de la recta tangente a ese punto sea -3
Calculamos la derivada de la función:
La derivada de la función en un punto cualquiera será:
La igualamos al valor de la pendiente:
Y nos queda una ecuación de primer grado, de la que tenemos que despejar X0, que es la coordenada x del punto que estamos buscando:
Para calcular la coordenada «y», obtenemos el valor de la función para x=-1, por lo que sustituimos la x por -1 en la función y operamos:
El valor de la función en x=-1 es 0, por lo que la coordenada y=0.
Ya tenemos la coordenadas del punto y el valor de la pendiente:
En la ecuación punto pendiente:
Sustituimos la pendiente y las coordenadas del punto por sus valores:
Operamos:
Y llegamos finalmente a la ecuación de la recta tangente que cumple las condiciones que nos pide el resultado.
Vamos a resolver otro ejercicio de este estilo, un poco más complicado.
Ejercicio 3
Hallar, si existen, las coordenadas «x» e «y» de los puntos sobre la curva definida por la fórmula:
Donde la recta tangente es paralela a la recta «r», cuya ecuación es:
Este ejercicio es muy similar al anterior, solo que los cálculos son algo más complejos. Además no nos están pidiendo la ecuación de la recta, sino las coordenadas de los puntos donde la recta es tangente.
Empezamos calculando la pendiente de la recta que nos da el enunciado. Para ello debemos despejar la y:
Separamos la fracción en dos términos y el valor de la pendiente es la fracción que queda delante de la x:
Como es paralela a la recta tangente que estamos buscando, la pendiente de la recta tangente es la misma:
Al igual que en el ejercicio anterior, la pendiente de la recta tangente a un punto de la cura, será igual al valor de la derivada en ese punto:
Por lo que a partir de esta igualdad, obtendremos los valores de x para los que la pendiente tiene ese valor.
Vamos a calcular la derivada de la función. En este caso tenemos un cociente dos funciones:
La derivada de un cociente es igual a la siguiente fórmula:
Aplicamos la fórmula:
Y operamos (mucho cuidado el signo menos que separa ambos términos en el denominador):
La derivada de la función en cualquier punto será:
Igualamos esta derivada a la pendiente calculada anteriormente:
Nos queda una ecuación de la que tenemos que despejar X0.
En primer lugar multiplicamos en cruz para eliminar los denominadores:
Pasamos todos los términos al mismo miembro:
Operamos:
Hemos llegado a una ecuación de segundo grado completa, que pasamos a resolver:
Obtenemos dos soluciones de x: x1=5 y x2=1
Para obtener la coordenada «y» de para cada valor x, calculamos el valor de la función:
Primero sustituimos la x por 5 y operamos:
El valor de «y» es -5/2, por lo que el primer punto donde la recta es tangente es:
Hacemos lo mismo con x=1
Por lo que las coordenadas del otro punto son:
Ejercicio 4
Calcula los valores de a, b y c en la función f(x)=ax²+bx+c, sabiendo que pasa por el punto (0,1) y que la pendiente de la recta tangente en el punto (2,-1) es igual a 0.
Tenemos la siguiente función:
Si pasa por el punto (0,1) quiere decir que el valor de la función en x=0 es 1:
Para obtener el valor de la función en x=o, sustituimos la x por 0 y la igualamos a 1:
De donde obtenemos el valor de c:
Por otro lado, el enunciado también nos habla de la pendiente en el punto (2,-1), lo que quiere decir que la función también pasa por ese punto, por lo que la función en x=2 es igual a -1:
Para obtener el valor de la función en x=2, sustituimos la x por 2 y la igualamos a -1:
Operamos y sustituimos c por su valor. Nos queda:
Dejamos los términos con a y b en el primer miembro y pasamos los números al segundo miembro:
Tenemos una ecuación que depende de a y b. Necesitamos otra ecuación para formar un sistema de dos ecuaciones con dos incógnitas y poder hallar sus valores.
La pendiente de la recta tangente a la función en un punto es igual al valor de la derivada en ese punto. En primer lugar, obtenemos la derivada de f(x):
El enunciado nos dice que la pendiente en x=2, es igual a 0, o lo que es lo mismo:
Para obtener el valor de la derivada en x=2, sustituimos la x por 2 y la igualamos a 0:
Operamos y nos queda:
Ya tenemos la segunda ecuación que nos faltaba, que junto con la anterior, forma el siguiente sistema, que pasamos a resolver:
De la segunda ecuación despejamos b:
Sustituimos la expresión de b en la primera ecuación:
Operamos para eliminar el paréntesis:
Operamos en el primer miembro:
Despejamos «a» y resolvemos:
Este valor de «a» lo sustituimos en la expresión donde despejamos b:
Sustituimos y operamos, llegando al valor de b:
Por tanto los valores de a, b y c son:
Ejercicio 5
Calcular a y b en la siguiente función:
para que pase por el punto (1,3) y para que y=4x+1 sea una recta tangente.
Que pase por el punto (1,3) significa que el valor de la función cuando x=1 es igual a 3:
Sustituimos x por 1 en la función e igualamos a 3:
Nos queda la siguiente ecuación:
Necesitamos otra ecuación para poder calcular el valor de a y b.
Por otro lado nos dice que la recta y=4x+1 es tangente a la función, cuya pendiente es igual a 4:
Ese valor de la pendiente es igual a la derivada de la función en el punto donde la recta es tangente:
Realizamos la derivada de la función:
En el punto donde la recta es tangente, nos queda la siguiente ecuación, de donde desconocemos el punto X0:
La recta no puede ser tangente en (1,3), ya que (1,3) no pertenece a la recta:
Necesitamos encontrar un punto que pertenezca tanto a la recta como a la función y para ello debemos fijarnos en lo siguiente: la función es impar, ya que los exponentes de todos sus términos son impares:
Al saber que es impar, sabemos que es simétrica con respecto al origen y por tanto, si (1,3) pertenece a la función, entonces el punto simétrico con respecto al origen de (1,3) también pertenecerá. Es decir, el simétrico de (1,3) con respecto al origen es (-1,-3) y este punto también pertenece a la función:
Además, (-1,-3) también pertenece a la recta:
Por lo que hemos encontrado un punto en común de la recta y la función. Por tanto, la recta es tangente a la función en x=1:
Sustituimos este valor de x en la ecuación anterior:
Y obtenemos la otra ecuación que depende de a y b:
Resolvemos el sistema formado por las dos ecuaciones y obtenemos su valor:
Ejercicio 6
De la siguiente función:
Sabemos que pasa por el punto (1,1) y en ese punto tiene tangente paralela a la recta 3x+y=0. Halla el valor de «a» y b.
Nos dicen que la función pasa por el punto (1,1), lo que quiere decir que cuando x=1, el valor de la función es 1, es decir:
Por tanto, calculamos f(1):
E igualamos f(1) a 1:
Nos queda una ecuación con dos incógnitas.
Por otro lado, nos dicen que la recta tangente en ese punto es paralela a esta otra recta:
Por tanto, vamos a obtener la pendiente de esta recta. Para obtener la pendiente, despejamos «y» y el valor que queda delante de la x es la pendiente:
En nuestro caso, la pendiente es igual a -3.
Además, la pendiente es igual a la derivada de la función en el punto x=1:
Por tanto, hallamos la derivada de la función:
Hallamos la derivada de la función en x=1, sustituyendo la x por 1:
E igualamos f'(1) a -3:
Nos queda otra ecuación con dos incógnitas, que junto con la ecuación anterior, formamos un sistema de dos ecuaciones con dos incógnitas, que resolvemos y nos queda:
Sustituyendo los valores de «a» y b en la función, tenemos la función que cumple las condiciones del enunciado:
Ejercicio 7
Calcula el valor de los coeficientes a, b y c de la siguiente función:
Sabiendo que:
a) La ecuación de la recta tangente a la función en x=0 es y=x
b) Tiene un extremo relativo en el punto (-1,0)
La ecuación de la recta tangente en x=0 es y=x, de donde podemos obtener directamente que el valor de la pendiente es igual a 1:
La pendiente es igual a la derivada en x=0:
Derivamos la función:
Y obtenemos la derivada de la función en x=0:
Igualando f'(0) a 1 nos queda directamente que c=1:
Por otro lado nos dicen que la función tiene un extremo relativo en el punto (-1,0), es decir, cuando x=-1. Que la función tenga un extremo relativo en x=-1, significa que la derivada primera en x=-1 es igual a 0:
Obtenemos la derivada de la función en x=-1, sustituyendo la x por -1:
Resolvemos las potencias:
Operamos en cada término:
Sustituimos c por su valor, que es 1:
Y operamos:
Finalmente, igualamos el valor de f'(-1) a 0:
Nos queda una ecuación que depende de «a» y b. Como tenemos dos incógnitas, necesitamos otra ecuación para poder resolver el sistema y hallar los valores de «a» y b.
Cuando nos dicen que la función tiene un extremo relativo en el punto (-1,0), además de decirnos que la derivada en x=-1 es 0, nos están dando otra pista y es que el valor de la función (sin derivar) en x=-1 es 0, es decir, cuando x=-1, el valor de la función es igual a 0:
Hallamos por tanto f(1), sustituyendo la x por 1 en la función original:
Resolvemos las potencias:
Operamos en cada término:
Sustituimos c por su valor, que es 1:
Operamos:
E igualamos f(1) a 0:
Ya tenemos la otra ecuación buscada.
Por último resolvemos el sistema formado por ambas ecuaciones:
La función que nos queda sustituyendo los coeficientes por sus valores es:
Ejercicio 8
La recta y=4x+k es tangente en el punto P a la siguiente curva:
a) Calcula el valor de k
b) Hallar la ecuación de la recta normal a la curva en el punto P
Tenemos la siguiente función:
De la ecuación de la recta, obtenemos el valor de la pendiente, que es el número que queda delante de la x:
Por otro lado, la pendiente en cualquier punto de la curva es igual al valor de la derivada en ese punto:
Calculamos la derivada de la función:
La derivada de la función en un punto cualquiera será:
Igualamos la derivada en un punto cualquiera al valor de la pendiente:
Y despejamos X0:
Una vez tenemos el valor de X0, el valor de Y0 lo obtenemos calculando el valor de la función en x=0:
Nos queda que Y0=3 y por tanto las coordenadas del punto P son:
Ahora vamos a calcular la ecuación de la recta tangente a la curva en ese punto.
En la ecuación punto pendiente:
Sustituimos la pendiente y las coordenadas del punto por sus valores:
Operamos y despejamos la «y»:
Por tanto, el valor de k en la ecuación del enunciado será igual a 3:
La ecuación de la recta normal a la curva en un punto es la siguiente:
Donde en esta caso, la pendiente de la recta normal es:
Obtenemos su valor sustituyendo m por 4:
Sustituimos la pendiente y las coordenadas del punto por sus valores:
Operamos y despejamos la «y»:
Ejercicio 9
Dada la siguiente función:
calcula los valores de a y b sabiendo que f(x) pasa por el punto (1,0) y que la tangente a la f(x) en x=1 tiene como pendiente -1.
Tenemos la siguiente función:
Y nos dice que pasa por el punto:
lo que quiere decir que cuando x=1, f(x)=0, lo que es lo mismo f(1)=0. Por tanto, sustituimos x por 1 y f(x) por 0 en la función:
Operamos y nos queda una ecuación con dos incógnitas:
Por otro lado nos dicen que la tangente es igual a -1 en x=1:
Como la pendiente es igual a la derivada de la función en x=1 donde tenemos:
Así que hallamos la derivada de la función:
Sustituimos x por 1 para calcular la derivada de la función en x=1:
Operamos e igualamos f'(1) a -1:
Nos queda otra ecuación con dos incógnitas, que junto con la ecuación anterior, formamos un sistema de dos ecuaciones con dos incógnitas, que resolvemos y cuya solución es:
Ejercicio 10
En la siguiente función:
calcula el valor de «a» para que la función tenga un extremo de valor -1.
Tenemos la siguiente función:
La función tendrá un extremo de valor -1, o lo que es lo mismo, tendrá un extremo en el siguiente punto:
en el que no conocemos la coordenada x, la cual calcularemos para poder despejar el valor de a.
Por otro lado, tal y como indico en la lección de cómo calcular máximos, mínimos y puntos de inflexión, la derivada en esos puntos es igual a cero, ya que la pendiente de la recta tangente en esos puntos es horizontal:
Con este dato, podemos calcular el valor de X0.
Obtenemos la derivada de la función:
Sustituimos x por X0 en la derivada para obtener f'(X0) y la igualamos a 0, ya que es el valor de la pendiente:
Y despejamos X0:
Por tanto, la función tiene un extremo en el punto (3,-1):
Una vez conocemos el punto, sustituimos en la función la x por 3 y f(x) por -1:
Nos queda una ecuación en la que tenemos «a» como incógnita:
Despejando a nos queda:
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: