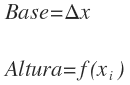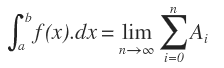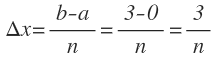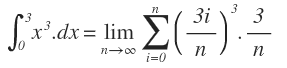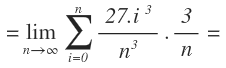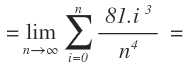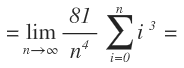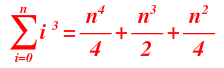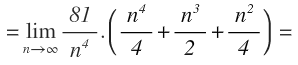En esta lección te voy a explicar cómo obtener la expresión para calcular una integral definida utilizando las sumas de Riemann.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Interpretación geométrica de las sumas de Riemann
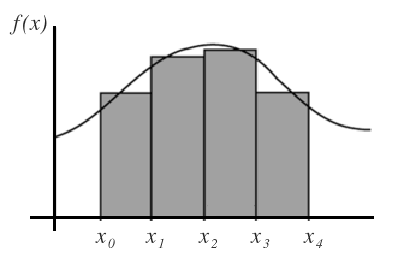
Una integral definida en un intervalo [a,b] nos da el valor del área encerrada entre una función f(x) y el eje x en un intervalo [a,b], siempre que la función sea continua.
Otra forma de calcular el área encerrada debajo de una curva, sería dividiendo el área en rectángulos iguales y sumando el área de cada uno de los rectángulos, aunque este cálculo sería aproximado:
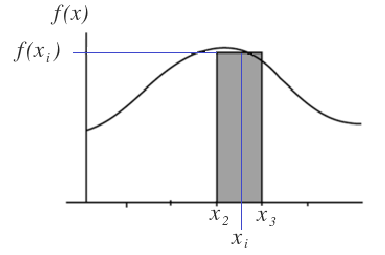
Si cogemos uno de esos rectángulos:
La base sería la diferencia de dos valores de x y la altura sería el valor de la función para X=Xi
El área de cada rectángulo la obtendríamos multiplicando la base por la altura y quedaría:
Si los rectángulos los hacemos cada vez más pequeños, el cálculo del área se hace cada vez más exacto
Y si los rectángulos los hacemos infinitamente pequeños y tenemos infinitos rectángulos, la suma infinita de esos rectángulos sería el área exacta del área encerrada debajo de esa función y sería igual a la integral definida de esa función para un intervalo [a,b]:
De donde obtenemos la expresión utilizada para resolver integrales definidas por sumas de Riemann, en la que, como hemos visto antes, el área de cada rectángulo sería igual a:
Donde el valor del incremento de x para un intervalo [a,b] lo definiremos como:
Y el valor de Xi como:
Todo esto se entiende mucho más claro con un ejemplo, que es lo que vamos a ver a continuación
Ejemplo de cómo obtener la expresión para calcular una integral por las sumas de Riemann
Obtener la expresión de las sumas de Riemann de la siguiente integral:
La función en este caso es:
Para un intervalo [0,3], por tanto a=0 y b=3.
Definimos el incremento de x para ese intervalo:
Y con esta expresión de incremento de x, calculamos Xi:
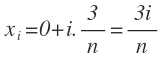
Calculamos el área de cada rectángulo, multiplicando las expresiones obtenidas de f(Xi) y del incremento de x:
Y nos queda:
Por lo que el valor de la integral por sumas de Riemann es:
Y para obtener el resultado del área, tendríamos que resolver el límite del sumatorio, que lo veremos en el siguiente apartado.
Cómo resolver una integral por las sumas de Riemann
Vamos a resolver la expresión que nos quedó en el apartado anterior y por tanto resolveremos la integral por sumas de Riemann.
Partimos de la expresión anterior:
Resolvemos el paréntesis elevando al cubo:
Y multiplicamos ambas fracciones:
Lo sea constante lo podemos sacar fuera del sumatorio. Todo lo que no lleve i, se considera constante, por lo que sacamos los términos que no llevan i fuera del sumatorio:
Llegados a este punto el sumatorio de i elevado al curo desde i=0 hasta n es igual a esta fórmula:
Se puede demostrar pero no es el objetivo de esta lección.
Sustituimos el sumatorio por su expresión, según la fórmula anterior:
Multiplicamos el paréntesis:
Y simplificamos términos:
Y al resolver el límite nos queda:
El resultado está en unidades cuadradas porque estamos calculando un área.
Para demostrar que el resultado es correcto, voy a resolver la integral definida por la regla de Barrow:
Y como no podía ser de otra forma, el resultado es el mismo.
Fórmula de sumatorios para resolver sumas de Riemann
Por último, te dejo aquí las fórmulas de los sumatorios desde le sumatorio de 1 hasta el sumatorio de i al cubo (que hemos utilizado en el ejemplo), desde 1=0 hasta n, que vas a necesitar para resolver integrales con las sumas de Riemann:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: