A continuación te voy a explicar cómo abatir un rectas y puntos en el sistema diédrico, con varios ejemplos explicados paso a paso.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Cómo abatir rectas en el plano de proyección horizontal en el sistema diédrico
Una vez sabemos cómo abatir un plano en diédrico, vamos a ver cómo abatir, en el plano de proyección horizontal, rectas contenidas en un plano, paso a paso.
Lo veremos con varios ejemplos.
Ejemplo 1: Cómo abatir una recta oblicua contenida en un plano oblicuo
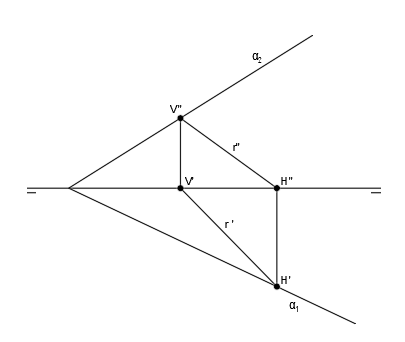
Tenemos representado en diédrico un plano oblicuo y una recta contenida en él:
Vamos a abatir la recta sobre el plano de proyección horizontal.
En primer lugar, abatimos el plano:
Ahora vamos a abatir la recta.
Para abatir la recta, vamos a aplicar el concepto de afinidad, teniendo en cuenta que todos los elementos afines son en realidad los elementos abatidos contenidos en el nuevo plano.
La traza horizontal del plano α1 será el eje de afinidad y la dirección de afinidad será la recta que une el punto V’ con el punto (V), siendo (V) el punto afín a V’. En este caso, podemos considerar a (α) como la recta afín a la línea de tierra:
Para poder obtener la dirección de afinidad necesitamos al menos un punto afín y en estos casos, siempre tendremos el punto (V) como punto afín a V’.
La recta afín a la recta r’ que obtengamos será la recta abatida.
Vemos que la recta r’ une los puntos V’ y H’, luego la recta afín unirá los puntos (V) y (H). Sabemos que en los puntos que pertenecen al eje de afinidad son puntos afines de sí mismos, luego como H’ está en el eje de afinidad, coincide con (H).
Así que, para obtener la recta afín de r’ (o la recta abatida) sólo tenemos que unir (V) con H’, dando como resultado la recta (r):
La recta abatida (r) se encuentra en verdadera magnitud, por lo que si medimos cualquier segmento en ella, será la longitud real.
Ejemplo 2: Cómo abatir una recta oblicua contenida en un plano oblicuo
Vamos a ver ahora otro ejemplo, donde no es tan intuitivo visualmente obtener la recta abatida, aunque el procedimiento a seguir sea el mismo que para el ejemplo anterior.
Si te cuesta verlo y te saliera un abatimiento como éste en algún examen, te recomiendo que plantees el mismo ejercicio con el plano del ejemplo anterior y después sigas los mismos pasos con el plano original.
Tenemos en diédrico el siguiente plano y tenemos que abatir la recta contenida en él:
Empezamos abatiendo el plano:
Una vez tenemos el plano abatido, seguimos abatimos la recta mediante afinidad, teniendo claros el eje de afinidad y la dirección de afinidad:
En este caso no se ven tan claro que el punto (V) es el afín de V’ al estar ambos puntos en el mismo lado del eje de afinidad.
Igual que en el ejemplo anterior, la recta r’ une los puntos V’ y H’, así que la recta afín (r) unirá los puntos (V) y H’:
Ejemplo 3: Cómo abatir una recta horizontal de plano contenida en un plano oblicuo
Hemos visto cómo abatir una recta contenida en un plano, de la que teníamos sus trazas, por lo que luego, en el plano abatido, para hallar la recta abatida sólo teníamos que unir las trazas abatidas.
Pero, ¿cómo abatimos una recta horizontal o vertical de plano, donde una de sus proyecciones es paralela a la traza del plano?
Vamos a ver un ejemplo de cómo abatir una recta horizontal de plano. Con la recta vertical se procedería de forma análoga.
Tenemos el siguiente plano en diédrico y una recta horizontal contenida en él:
Abatimos el plano:
Distinguimos el eje y la dirección de afinidad para tenerlos claros:
Vemos que r’ es paralela a la traza horizontal del plano α1 (eje de afinidad) y que nace desde V’, así que la recta afín o recta abatida (r) también será paralela al eje de afinidad y partirá del punto afín de V’, que es (V):
Ejemplo 4: Cómo abatir una recta horizontal de plano contenida en un plano oblicuo
Por último, vamos a ver cómo abatir una recta horizontal de plano contenida en el plano oblicuo que no es tan intuitivo de ver los elementos afines o abatidos:
Abatimos el plano:
Distinguimos eje y dirección de afinidad:
La recta abatida (r) será paralela a al eje de afinidad, partiendo de (V):
Cómo abatir rectas en el plano de proyección vertical en el sistema diédrico
Una vez sabemos cómo abatir una recta sobre el plano de proyección horizontal, vamos a ver cómo hacerlo sobre el plano vertical.
Tenemos la siguiente recta contenida en un plano:
Vamos a abatir la recta sobre el plano de proyección vertical.
En primer lugar abatimos el plano:
Reconocemos el eje y la dirección de afinidad:
Y unimos (H) con V” para obtener la recta abatida (r):
Cómo abatir un punto en el sistema diédrico
Para terminar, vamos a ver cómo se abate un punto en el sistema diédrico.
Para abatir un punto en diédrico, en necesario que el punto esté contenido dentro de un plano y por tanto, que pertenezca a una recta contenida en el plano.
Vamos a ver un par de ejemplos.
Ejemplo 1
Tenemos un plano y un punto representados en diédrico:
Primero comprobamos que el punto pertenece al plano, mediante una recta horizontal de plano:
El punto pertenece a la recta, que está contenida en el plano, por lo que el punto pertenece a la recta.
Abatimos el plano aprovechando la traza vertical de la recta:
Distinguimos el eje y la dirección de afinidad:
Para poder abatir el punto A, antes necesitamos abatir la recta que contiene al punto. Por tanto, abatimos la recta s, dando como resultado (s):
El punto abatido estará ubicado en la recta abatida (s).
Desde A’, trazamos una línea paralela a la dirección de afinidad:
El punto de corte de la línea paralela a la dirección de afinidad, con la recta abatida, dará lugar al punto abatido (A):
Vamos a ver cómo abatir otro punto perteneciente a ese plano, el punto B:
Comprobamos que el punto B pertenece al plano con una recta horizontal de plano t:
Ahora abatimos la recta t, para lo cual, necesitamos abatir el punto Vb’, contenido en (α). Trazamos una paralela a la dirección desde Vb’ hasta cortar con (α), que será el punto (Vb):
Desde (Vb) y paralela al eje de afinidad, trazamos la recta abatida (t), donde se encontrará el punto abatido (B), en el punto de corte de esta recta con la línea de dirección de B:
Ejemplo 2
Vamos a ver otro ejemplo de abatimiento de puntos en diédrico, en el plano que no es tan intuitivo visualmente:
Comprobamos que el punto A pertenece al plano:
Abatimos el plano:
Distinguimos la dirección de afinidad:
Desde el punto A’ trazamos una línea paralela a la dirección de afinidad:
Abatimos la recta r que contiene al punto A:
El punto de corte de la recta (r) con la línea de dirección dará como resultado el punto abatido (A):
Vamos a ver cómo abatir otro punto que pertenezca también al plano:
Comprobamos que B pertenece al plano con la recta horizontal de plano t:
Tenemos que abatir la recta t, para lo que necesitamos abatir antes el punto Vb’, contenido en (α). Así que, trazamos una paralela a la dirección desde Vb’ hasta que corte con (α), dando lugar al punto (Vb):
Finalmente, partiendo de (Vb), trazamos una recta paralela al eje de afinidad, que es la recta abatida (t). En el punto de corte de esta recta con la línea de dirección del punto B, se encontrará el punto abatido (B), :
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE