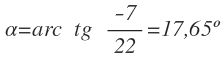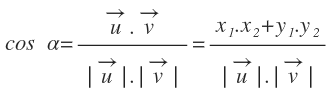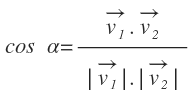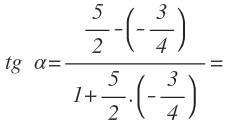A continuación te voy a explicar qué es el ángulo formado entre dos rectas y cómo calcular el ángulo de dos rectas que se cortan en un plano. Existen dos métodos para calcularlo. Veremos cada uno paso a paso con ejercicios resueltos.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Ángulo de dos rectas
En un plano, dos rectas puede ser:
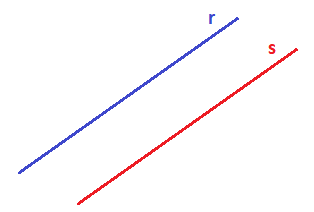
Paralelas: Si no tienen ningún punto en común
Coincidentes: Si todos sus puntos son comunes, es decir, una recta está encima de la otra:
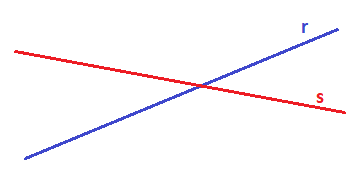
Secantes: Si las rectas se cortan en un punto:
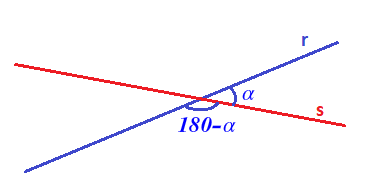
En el caso de que las rectas se corten en un punto, forman cuatro ángulos entre ellas, iguales dos a dos: dos ángulos menores y dos ángulo mayores. Un ángulo menor y un ángulo mayor son ángulossuplementarios, por lo que al menor le llamaremos α y al mayor (180-α):
Se le llama ángulo que forman dos rectas al menor de los ángulos que definen (al ángulo agudo), es decir al ángulo α.
Cómo calcular el ángulo de dos rectas que se cruzan
Una vez que hemos visto qué es el ángulo entre dos rectas en el planos, vamos a ver cómo lo podemos calcular. Existen dos formas de hacerlo: en función de sus pendientes y en función de los vectores de dirección de las rectas. Vamos a ver cada uno de ellos y luego puedes utilizar con el que más cómodo te sientas:
Ángulo de dos rectas en función de sus pendientes
Dos rectas r y s, de pendientes m1 y m2 respectivamente, forman un ángulo cuya tangente vale:
Esta fórmula se puede demostrar, partiendo de que la pendiente de una función es igual a la tangente de α, pero la he puesto directamente para ir más al grano.
Despejando α en la fórmula anterior, mediante la inversa de la tangente nos queda el ángulo que forman en entre las dos rectas:
Para utilizar este método, es conveniente pasar las rectas a su forma explícita, para identificar más claramente cuál es la pendiente de cada recta.
Vamos a ver un ejemplo: Calcular el ángulo formado por las siguientes rectas:
Pasamos a su forma explícita la primera ecuación de la recta:
Para ello, primero despejamos el término que contiene a la «y»:
Y despejamos la «y»:
Por último, separamos el segundo miembro en los dos términos que tenemos en el numerador, dejando el mismo denominador en cada miembro y ya la tendremos en forma explícita. Una vez así, la pendiente es el coeficiente que queda delante de la «x»:
La segunda recta ya está en forma explícita, por tanto podemos obtener directamente su pendiente:
Ahora vamos a utilizar la fórmula para calcular el ángulo que forman las dos rectas:
Sustituimos cada pendiente por su valor:
Y operamos:
Finalmente con la función inversa de la tangente obtenemos el ángulo:
Como ves, en este ejemplo, hemos obtenido un valor determinado para el ángulo, pero pueden ocurrir los siguientes casos:
- Que no exista tg α o que en la fórmula, el denominador sea igual a 0: En ese caso el ángulo que forman las dos rectas es igual a 90º y por tanto son perpendiculares.
- Que tg α sea igual a 0: En ese caso las rectas son paralelas o coincidentes y el ángulo que forman es igual a 0º. (Habría que resolver el sistema para determinar si las rectas son paralelas o coincidentes).
- Si la tg α es igual a un valor concreto, las rectas son secantes (que es el caso del ejemplo)
Ángulo de dos rectas en función de sus vectores de dirección
Otra forma de calcular el ángulo que forman dos rectas es mediante sus vectores de dirección. El ángulo que forman dos rectas es el mismo ángulo que forman sus respectivos vectores de dirección:
Por otro lado, el producto escalar de dos vectores es igual a:
De donde podemos despejar el coseno del ángulo:
Si conocemos las coordenadas de los vectores:
Podemos obtener su producto escalar mediante su expresión analítica:
Combinando ambas expresiones, podemos llegar a obtener el valor del coseno del ángulo:
Y una vez tengamos el valor del coseno, podemos calcular el valor del ángulo mediante su inversa.
Para utilizar este método, debemos obtener previamente los vectores de dirección de cada recta. Una forma es pasando la ecuación de la recta a su forma general o implícita:
Donde su vector de dirección lo podemos obtener a partir de los coeficientes A y B:
Si tenemos las ecuaciones de las rectas en forma paramétrica o contínua, los vectores pueden obtenerse más directamente.
Vamos a ver un ejemplo: Calcular el ángulo formado por las siguientes rectas:
Las rectas son las mismas que en el ejemplo anterior. En primer lugar obtenemos el vector de dirección de la primera recta, que al estar en forma general, lo podemos obtener directamente:
Ahora vamos a obtener el vector de dirección de la segunda recta:
Convertimos esta ecuación a su forma general, pasando todo a un miembro y ordenando términos, de donde ya podemos obtener su vector director:
Una vez tenemos los dos vectores, ya podemos aplicar la fórmula:
Empezamos calculando el producto escalar mediante su expresión analítica, que corresponde al numerador de la fórmula anterior:
Sustituimos las coordenadas de cada vector en la fórmula:
Y operamos:
Seguimos calculando los módulos de cada vector.
El módulo del vector de dirección de la primera recta es:
El módulo del vector de dirección de la segunda recta es:
Ya tenemos todos los datos para poder calcular el valor del coseno del ángulo:
Que despejando el ángulo, mediante la función inversa de seno, llegamos al valor del ángulo entre los vectores:
Que como verás es el mismo valor que nos salía con el otro procedimiento.
Utilizando este método, podemos tener los siguientes casos:
- Que el coseno del ángulo sea igual a 0 (cos α=0): En este caso el ángulo es 90º, por lo que las rectas son perpendiculares.
- Que el coseno del ángulo esté entre 0 y 1: Las rectas son secantes
- Que el coseno del ángulo sea igual a 1 (cos α=1): En este caso, el ángulo que forman las rectas es de 0º y por tanto las rectas son paralaleas o coincidentes (Habría que resolver el sistema para determinar si las rectas son paralelas o coincidentes)
Ejercicios resueltos sobre el ángulo de dos rectas
Ejercicio 1
Calcula el ángulo que forman las siguientes rectas:
Esta vez, voy a hallar el ángulo que forman las rectas con el método de sus vectores directores, ya que se pueden obtener fácilmente.
El vector de dirección de la primera recta es:
El vector de dirección de la segunda recta es:
Una vez tenemos los vectores, ya podemos aplicar la fórmula:
Calculamos el producto escalar de los vectores mediante su expresión analítica:
Calculamos los módulos de los vectores de dirección de cada recta:
Sustituimos en la fórmula:
Y por último calculamos el ángulo haciendo la inversa del coseno:
Las rectas forman un ángulo de 0º, porque lo que serán paralelas o coincidentes.
Ejercicio 2
Calcula el ángulo que forman las siguientes rectas:
Al igual que en el ejercicio anterior, al tener las rectas en forma continua también resulta fácil obtener sus vectores de dirección, que son:
Utilizamos por tanto el método de calcular el ángulo entre dos rectas con la fórmula obtenida a partir de sus vectores de dirección:
El valor del producto escalar de los vectores es:
Y los módulos de los vectores son:
Sustituimos los datos en la fórmula y operamos:
El ángulo por tanto es:
Es decir, las rectas son perpendiculares.
Ejercicio 3
Calcula el ángulo que forman las siguientes rectas:
Este ejercicio lo vamos a resolver con el método de las pendientes.
La primera ecuación de la recta:
La convertimos a su forma explícita y obtenemos su pendiente:
Con la ecuación de la segunda recta:
Hacemos lo mismo:
Aplicamos la fórmula de las pendientes:
Sustituimos cada pendiente por su valor:
Y operamos:
Haciendo la inversa de la tangente obtenemos el ángulo:
Nos sale un ángulo negativo, pero es igual a considerar que el ángulo es positivo.
Ejercicio 4
Calcula el ángulo que forman las siguientes rectas:
Este ejercicio también lo resolveremos con el método de las pendientes, ya que tengo las dos rectas en su forma explícita.
Las pendientes de las rectas son:
Aplicamos la fórmula:
Sustituimos cada pendiente por su valor:
Y operamos:
Un número dividido entre 0 no existe o es indeterminado.
Cuando la tangente de un ángulo no existe, quiere decir que el ángulo es de 90º:
Por tanto las rectas son perpendiculares.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: