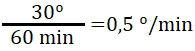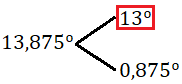A continuación vamos a ver cómo calcular el ángulo que forman las agujas de un reloj, con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
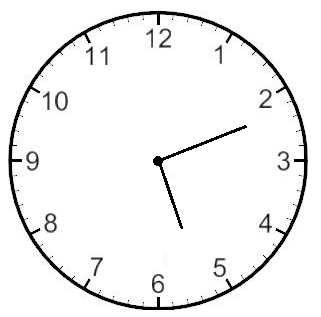
Te recuerdo, que la aguja más corta, que marca las horas se llama horario y la aguja más larga que marca los minutos se llama minutero.
Cómo calcular el ángulo del horario
Cuando el horario da una vuelta completa, es decir, parte desde las 12 h y vuelve a llegar a las 12 h, a recorrido 360º:
Entonces, ¿cuántos grados recorrerá el horario en una hora?
Para saber cuántos grados recorre el horario por hora, tenemos que dividir, los 360º de una vuelta completa entre las 12 horas que tiene el reloj:
Por tanto, por cada hora el horario avanza 30º.
Por tanto, para calcular el ángulo que forma el horario en una hora, tenemos que multiplicar el número de horas que han pasado por 30º.
Por ejemplo, a las 4 h, ¿qué ángulo formará el horario?
Pues solo tenemos que multiplicar las 4 horas que han pasado por los 30º que recorre en cada hora:
Por otro lado, hay que tener en cuenta que el horario no sólo se coloca justo en las horas en punto, sino que entre una hora y otra también se va moviendo por cada minuto que pasa.
¿Cuántos grados se mueve el horario por cada minuto?
Ya sabemos que el horario recorre 30º entre una hora y otra. Como en 1 hora hay 60 minutos, para saber cuántos grados se mueve el horario por minuto, tenemos que dividir los 30º entre los 60 minutos:
Por tanto, por cada minuto el horario avanza 0,5º.
Así que para calcular el ángulo que forma el horario, además de multiplicar el número de horas que han pasado por 30º, también hay que multiplicar los minutos que tenemos por 0,5º
Por ejemplo, a las 4 h 42 min, ¿qué ángulo formará el horario?
Para calcular el ángulo del horario a las 4 h 42 min, multiplicamos las 4 horas por 30º y sumarle los 42 minutos por 0,5º:
Al igual que el horario se va moviendo por cada minuto, si queremos afinar todavía más, también podemos calcular los grados que recorre el horario por cada segundo que pasa.
¿Cuántos grados se mueve el horario por cada segundo?
El horario recorre 0,5º entre un minuto y otro. Como en 1 minuto hay 60 segundos, para saber cuántos grados se mueve el horario por segundo, tenemos que dividir los 0,5º entre los 60 segundos:
El horario avanza 0,00833º porcada segundo que pasa.
Así que si conocemos las horas, los minutos y los segundos, podemos calcular el ángulo exacto del horario, multiplicando las horas por 30º, los minutos por 0,5º y los segundos por 0,00833º y sumando cada una de las multiplicaciones.
Por ejemplo, a las 4 h 42 min 26 s, ¿qué ángulo formará el horario?
En este caso, para calcular el ángulo del horario, multiplicamos las 4 horas por 30º, le sumamos los 42 minutos por 0,5º y le sumamos también los 26 segundos por 0,00833º:
Cómo calcular el ángulo del minutero
El minutero da una vuelta completa por cada hora que pasa. Cuando el minutero da una vuelta completa, es decir, parte desde las 12 h y vuelve a llegar a las 12 h, a recorrido 360º:
¿Cuántos grados recorrerá el minutero en un minuto?
Para saber cuántos grados recorre el minutero en un minuto, dividimos los 360º de una vuelta completa entre los 60 minutos que tiene una hora:
Por cada minuto que pasa, el minutero avanza 6º.
Así que para calcular el ángulo que forma el minutero, sólo tenemos que multiplicar los minutos que hayan pasado por 6º.
En este caso, no nos influyen las horas, ya que por cada hora, el minutero vuelve al inicio
Por ejemplo, ¿qué ángulo formará el minutero cuando hayan pasado 18 minutos?
Calculamos el ángulo multiplicando los 18 minutos por los 6º que recorre cada minuto:
También podemos calcular cuántos grados se mueve el minutero por cada segundo que pasa.
¿Cuántos grados se mueve el minutero por cada segundo?
El minutero recorre 6º de un minuto a otro. Como en 1 minuto hay 60 segundos, para saber cuántos grados se mueve el minutero por segundo, tenemos que dividir los 6º entre los 60 segundos:
Así que, por cada segundo que pasa, el minutero avanza 0,1º.
Así que para calcular el ángulo que forma el minutero, además de multiplicar el número de minutos por 6º, también hay que multiplicar los segundos que tenemos por 0,1º
Por ejemplo, ¿qué ángulo formará el minutero cuando hayan pasado 18 minutos y 36 segundos?
Para calcular el ángulo del minutero, multiplicamos los 18 minutos por 6º y sumarle los 36 segundos por 0,1º:
Cómo calcular el ángulo formado entre el horario y el minutero
Una vez sabemos cómo calcular el ángulo del horario y el ángulo del minutero, para saber qué ángulo se forma entre las dos agujas del reloj, al ángulo mayor le restamos el ángulo menor.
Tendrá el mayor ángulo la aguja que más adelantada esté, que podrá ser el horario o el minutero indistintamente.
Vamos a ver un ejemplo:
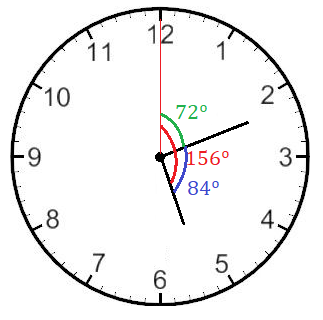
¿Qué ángulo forman las agujas del reloj a las 5 h 12 min?
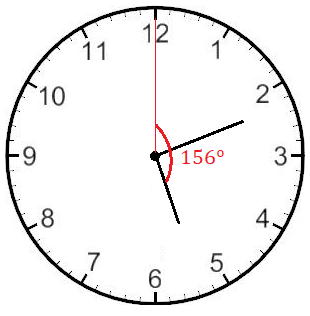
Calculamos el ángulo del horario:
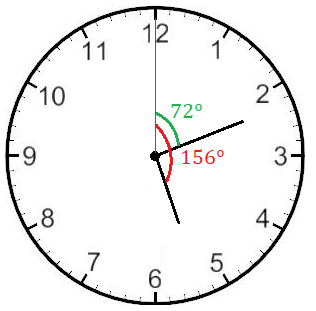
Calculamos el ángulo del minutero:
En este caso, el mayor ángulo es del horario, por tanto, al ángulo del horario le restamos el ángulo del minutero:
El ángulo que forman las agujas del reloj a las 5 h 12 min es de 84º:
Vamos a ver otro ejemplo:
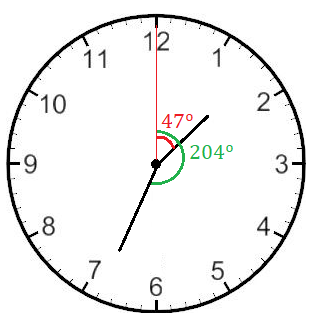
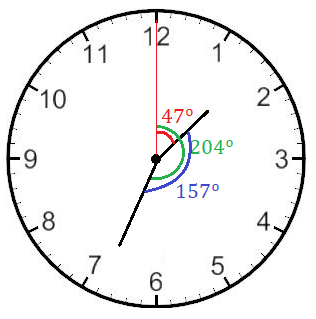
¿Qué ángulo forman las agujas del reloj a las 1 h 34 min?
Calculamos el ángulo del horario:
Calculamos el ángulo del minutero:
En este caso, el minutero está más adelantado que el horario, por lo que su ángulo es mayor. Para calcular el ángulo formado entre ambas agujas, restamos al ángulo del minutero el ángulo del horario:
Las agujas forman un ángulo de 157º:
Ejercicios resueltos de calcular el ángulo que forman las agujas de un reloj
Ejercicio 1
Calcula el ángulo que forman las agujas de un reloj a las 8 h 18 min:
El ángulo del horario es:
El ángulo del minutero es:
Restamos el ángulo del minutero al ángulo del horario:
Ejercicio 2
Calcula el ángulo que forman las agujas de un reloj a las 9 h 36 min:
Calculamos el ángulo del horario:
Calculamos el ángulo del minutero:
Al ángulo del horario le restamos el ángulo del minutero:
Ejercicio 3
Calcula el ángulo que forman las agujas de un reloj a las 7 h 52 min:
El ángulo del horario es:
El ángulo del minutero es:
El ángulo del minutero es el mayor, luego a este ángulo le restamos el ángulo del horario:
Ejercicio 4
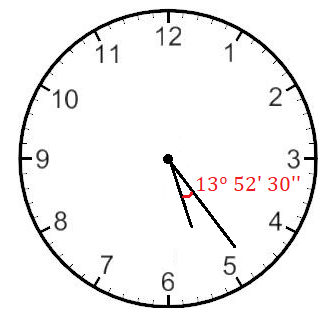
Calcula el ángulo que forman las agujas de un reloj a las 5 h 24 min 45 s:
En este ejercicio tenemos también los segundos.
Para calcular el ángulo del horario multiplicamos las 5 horas por 30º, le sumamos los 24 minutos por 0,5º y los 45 segundos por 0,00833º:
Calculamos el ángulo del minutero multiplicando los 24 minutos por 6º y sumándole los 45 segundos por 0,1º:
Al ángulo del horario le restamos el ángulo del minutero:
Aunque no es necesario, vamos a pasar esta medida a su forma compleja (tienes explicado en el Curso de Sistema Sexagesimal cómo hacerlo).
Separamos la parte entera de la parte decimal, quedando la parte entera como parte del resultado:
Pasamos los 0,875º a minutos multiplicando por 60:
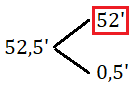
Separamos la parte entera de la parte decimal en los minutos:
Los 52′ correspondientes a la parte entera son parte del resultado y los 0,5′ los pasamos a segundos multiplicando por 60, que también son parte del resultado:
Por tanto, 13,875º es igual a 13º 52 minutos y 30 segundos:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: