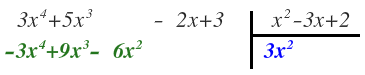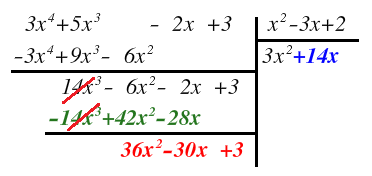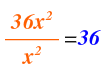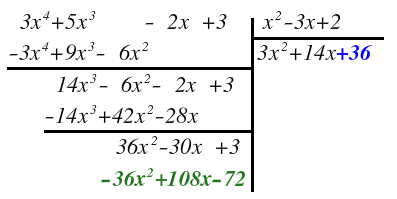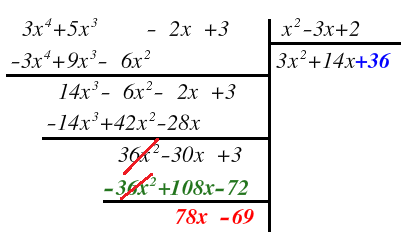A continuación te voy a explicar la división de polinomios. Te enseñaré cómo dividir un polinomio entre otro polinomio con el método general, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
La división de polinomios es uno de los temas que más dudas genera, debido a que hay que tener en cuenta muchos conceptos que normalmente no se terminan de entender y eso provoca que se vayan cometiendo numerosos errores.
Por eso, es muy importante que domines el resto de operaciones con monomios que tienes explicados en el Curso de Polinomios, ya que verás que lo vas a necesitar para realizar esta división.
Propiedades de la división de polinomios
Antes de seguir, para que entiendas mejor este método, vamos a recordar las partes que forman cualquier división, sea una división entre números o entre polinomios.
Cualquier división está formada por el dividendo, el divisor, el cociente y el resto:
Si estas partes, las escribimos en forma de polinomio, queda
Y cumplen las siguientes propiedades:
1- El grado del dividendo D(x) es mayor o igual que el grado del divisor d(x):
2- El grado del dividendo D(x) es igual al grado del divisor d(x) más el grado del cociente C(x):
3- El grado del resto R(x) es menor que el grado del divisor d(x):
4- El dividendo es igual al divisor por el cociente más el resto:
Si compruebas esta fórmula con una división de números, comprobarás que también se cumple.
División de polinomios
El método que te voy a explicar, corresponde al método general de división de polinomios, ya que existen más métodos para dividir polinomios, como por ejemplo el método o la regla de Ruffini, que veremos más adelante.
Este método sirve para dividir cualquier tipo de polinomios y para realizarlo hay que tener en cuenta las propiedades anteriores.
Si quieres ver la explicación en vídeo y no seguir leyendo el resto, aquí tienes un vídeo de cómo dividir polinomio entre polinomio con ejercicios resueltos paso a paso:
Si quieres que te quede más claro, vamos a resolver un ejemplo paso a paso:
El primer paso consiste en colocar y escribir correctamente el dividendo y el divisor para poder empezar su división.
En nuestro caso, el numerador es el dividendo y el denominador es el divisor.
Tanto el dividendo, como el divisor, los términos se escriben en orden decreciente de los grados de sus términos, es decir, empezando por el de mayor grado, hasta llegar al término de grado 0 (el término independiente).
En nuestro ejemplo, el dividendo no tiene término de grado 2, por lo que dejamos un espacio en su lugar. Nos queda así:
Una vez tenemos en su sitio el dividendo y el divisor, y con los correspondientes huecos de los términos que faltan, vamos a empezar a calcular el cociente.
Para ello, dividimos el primer término del dividendo entre el primer término del divisor:
Y lo colocamos en el cociente. Corresponde al primer término del cociente:
Ahora, debemos multiplicar este término del cociente por cada uno de los términos del divisor:
Los colocamos debajo del dividendo, pero cumpliendo éstas dos condiciones:
- Cada uno se coloca debajo de su término semejante, es decir, del término tenga el mismo grado o de su hueco correspondiente (en el caso de que el dividendo no tenga término de ese grado)
- Con el signo contrario
Nos queda de la siguiente manera:
Como dejamos un hueco para el término de grado 2, el 6x² lo colocamos debajo de ese hueco.
Y ahora en el dividendo, sumamos verticalmente las dos expresiones que tenemos:
Al tener cada término debajo de su término semejante del dividendo, esta suma se realiza de manera más ordenada. Es lo que buscamos también cuando dejamos el hueco en el dividendo del término que falte.
Al realizar esta suma, el término de mayor grado se anula, que es el objetivo de todos los pasos que hemos dado hasta ahora.
Llegados a este punto, nos ha quedado una nueva expresión algebraica en el dividendo cuyo grado es mayor que el grado del divisor.
Por tanto, seguimos dividiendo esta nueva expresión entre el divisor, repitiendo de nuevo todos los pasos:
Para calcular el segundo término del cociente, dividimos el primer término de la nueva expresión del dividendo, entre el primer término el divisor:
Y lo colocamos en el cociente. Corresponde al segundo término del cociente:
Ahora, igual que antes, multiplicamos este segundo término del cociente por cada uno de los términos del divisor y los colocamos en la parte del dividendo, debajo de su término semejante y con el signo contrario:
Sumamos verticalmente en el dividendo:
Anulando el término de mayor grado y obteniendo una nueva expresión, cuyo grado ahora es igual al grado del divisor, por lo que todavía podemos seguir dividiendo.
Volvemos a repetir el proceso para calcular el tercer término del cociente. Dividimos el primer término de la nueva expresión del dividendo, entre el primer término el divisor:
Y lo colocamos en el cociente, que corresponde al tercer término del cociente:
Seguimos multiplicando este tercer término del cociente por cada uno de los términos del divisor y los colocamos en la parte del dividendo, debajo de su término semejante y con el signo contrario:
Y volvemos a sumar verticalmente:
Ahora, la expresión resultante del dividendo tiene un grado menor que el grado del divisor. Por tanto, ya no podemos continuar, por lo que hemos terminado de dividir.
La última expresión que nos queda en la parte del dividendo, con grado menor que el grado del divisor, corresponde al resto R(x) y la expresión que hemos ido calculando, debajo del divisor, corresponde al cociente C(x).
Por tanto, el resultado de la división es el cociente C(x):
Y el resto R(x):
Si queremos expresar el dividendo D(x) en función del divisor d(x), del cociente C(x) y del resto R(x), lo podemos hacer siguiendo la cuarta propiedad de la división de polinomios:
Estos serían todos los polinomios que necesitamos:
Que si sustituimos nos queda:
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: