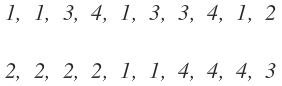A continuación te voy a explicar cómo hacer una tabla de frecuencias, según el tipo de datos estadísticos, ya sean aislados o agrupados en intervalos, con ejemplos resueltos paso a paso.
Si has llegado hasta aquí es porque quieres aprender cómo resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es una tabla de frecuencia
La tabla de frecuencia es una tabla donde los datos estadísticos aparecen bien organizados, distribuidos según su frecuencia, es decir, según las veces que se repite en la muestra.
En esta tabla se representan los diferentes tipos de frecuencias, ordenados en columnas.
La tabla de frecuencia es una herramienta que permite la realización de los gráficos o diagramas estadísticos de una forma más fácil.
Tipos de frecuencias
Antes de aprender a construir una tabla de frecuencias, debemos conocer los tipos de frecuencias que existen y cómo se calcula cada una de ellas. Existen frecuencias absolutas y relativas, así como frecuencias absolutas y relativas acumuladas.
Vamos a ver cada una de ellas más despacio:
Frecuencia absoluta
La frecuencia absoluta es el número de veces que un dato se repite dentro de un conjunto de datos. Se representa como fi, donde la «i» corresponde al número de dato.
La forma de obtener la frecuencia absoluta no es otra que contando las veces que aparece el dato en el conjunto de datos.
La suma de las frecuencias absolutas corresponde al número total de datos, representado por la letra N:
Frecuencia relativa
La frecuencia relativa de un dato es el número que se repite ese dato en relación al número total de datos, o en otras palabras, es la proporción de veces que aparece ese dato con respecto al total.
Se representa como «ni», siendo «i» el número de dato. y se calcula dividiendo la frecuencia absoluta de cada dato entre el número total de datos:
El valor de la frecuencia relativa siempre va a estar entre 0 y 1. El valor obtenido está en tanto por uno, pero lo podemos expresar en tanto por ciento si lo multiplicamos por 100.
La suma de todas las frecuencias relativas de todos los datos de la muestra es igual a 1 (cuando se expresa en tanto por 1, que es lo más común):
Frecuencia absoluta acumulada
La frecuencia absoluta acumulada es la suma de las frecuencias absolutas que se va acumulando hasta ese dato, es decir, la frecuencia absoluta acumulada de un dato en concreto se obtiene sumando su frecuencia absoluta a las frecuencias absolutas de los datos que son menores que él.
Se representa como «Fi», donde «i» es el número de dato.
Se calcula sumando la frecuencia absoluta de un dato más la frecuencia absoluta del dato anterior. Por tanto, la frecuencia absoluta acumulada del primer dato coincide con su frecuencia absoluta y la frecuencia absoluta acumulada del último dato coincide con el número total de datos.
Frecuencia relativa acumulada
La frecuencia relativa acumulada es el mismo concepto que para la frecuencia absoluta acumulada.
Se representa como «Ni», donde la «i» es el número de dato y se puede obtener como el cociente entre la frecuencia absoluta acumulada para cada dato entre el número de datos totales:
O también, como la suma de la frecuencia relativa de un dato más la frecuencia relativa del dato anterior. Así que, la frecuencia relativa acumulada del primer dato coincide con su frecuencia relativa y la frecuencia relativa acumulada es igual a 1.
Cómo construir una tabla de frecuencias con datos aislados o no agrupados. Ejemplo resuelto.
Si no quieres seguir leyendo, aquí tienes los dos ejemplos que vienen a continuación (cómo hacer una tabla de frecuencias con datos aislados y con datos agrupados) explicados paso a paso en formato vídeo por si te gusta más este formato:
O si lo prefieres puedes seguir leyendo (después de ver el vídeo o sin verlo):
Vamos a ver paso a paso cómo construir una tabla de frecuencias con datos aislados con el siguiente ejemplo:
En una urbanización se ha realizado una encuesta preguntando cuántos dormitorios tienen sus viviendas. Los resultados sobre el número de dormitorios por vivienda fueron los siguientes:
Obtener la tabla de frecuencias absolutas, relativas y acumuladas.
La tabla de frecuencias tendrá las siguientes 5 columnas:
- Datos (xi)
- Frecuencia absoluta (fi)
- Frecuencia absoluta acumulada (Fi)
- Frecuencia relativa (ni)
- Frecuencia relativa acumulada (Ni)
Vamos a ver cómo rellenar cada una de ellas.
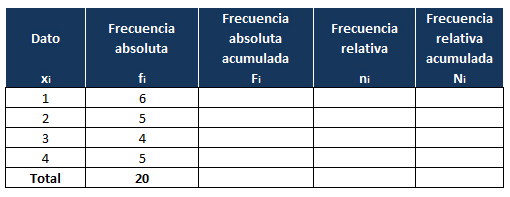
En la primer a columna, colocamos los valores de los datos pero sin repetir, ordenados de menor a mayor. En nuestro caso, tenemos varios 1, varios 2, varios 3 y varios 4, por lo que colocamos estos valores una vez en la tabla. Dejamos la última fila para colocar el total:
Ahora, vamos a obtener la frecuencia absoluta de cada uno de los valores. Para ello contamos las veces que se repite cada valor:
- El 1 se repite 6 veces
- El 2 se repite 5 veces
- El 3 se repite 4 veces
- El 4 se repite 5 veces
Colocamos cada valor en su casilla correspondiente y en la última fila, escribimos la suma de todas las frecuencias, que como puedes comprobar, también coincide con el número total de datos:
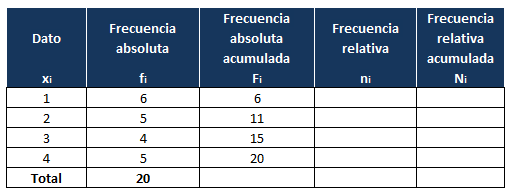
Vamos a obtener ahora la frecuencia absoluta acumulada de cada dato. En la primera fila, la frecuencia absoluta acumulada coincide con la frecuencia absoluta, es decir, ambas son 6.
Para el resto de filas, la frecuencia absoluta acumulada la obtenemos sumando la frecuencia absoluta acumulada del dato anterior (del dato de arriba) más su frecuencia absoluta (dato de su izquierda).
Por ejemplo, para el 2, la frecuencia absoluta acumulada es igual a 6, que es la frecuencia absoluta acumulada anterior, más 5 que es su frecuencia absoluta, cuyo resultado es 11. Para 3, 4 y 5 se calcula de la misma forma:
La frecuencia absoluta acumulada de 4 coincide con el número total de elementos.
Vamos ahora con la frecuencia relativa, que la calculamos con la siguiente fórmula:
Es decir, dividiendo cada frecuencia absoluta, entre el número total de elementos, que es 20 para todos, en este caso.
Por ejemplo, para el 1, la frecuencia relativa es:
Lo hacemos igual para el resto de datos y en la última fila, colocamos la suma de las frecuencias relativas:
Para obtener la frecuencia relativa acumulada, lo podemos hacer como para la frecuencia absoluta acumulada, es decir, la frecuencia relativa acumulada del primer dato es igual que su frecuencia relativa y para los datos siguientes es igual a su frecuencia relativa más la frecuencia relativa del dato anterior (del dato de arriba):
También la podemos calcular la frecuencia relativa acumulada, dividiendo cada frecuencia absoluta acumulada entre el número de elementos total:

Realizándose de la misma forma para el resto de datos.
La frecuencia relativa acumulada del 4 es igual a 1.
Cómo construir una tabla de frecuencias con datos agrupados en intervalos. Ejemplo resuelto.
Si tenemos un número muy grande de datos, éstos se agrupan en intervalos, para no tener que realizar tablas muy largas con muchos datos diferentes. También se agrupan en intervalos cuando las variables son continuas.
En estos caso se realiza una tabla de frecuencias con datos agrupados.
Los datos se agrupan en intervalos, llamados clases y es a estos intervalos los que se asignan sus frecuencias correspondientes.
Sobre las clases, debes conocer los siguientes conceptos:
- Límites de clase: Cada intervalo tiene un límite inferior, que pertenece a ese intervalo (cerrado por la izquierda con un corchete) y un límite superior que no pertenece (abierto por la derecha)
- Amplitud de clase: La amplitud es la diferencia entre el límite superior e inferior y debe ser la misma para cada intervalo
- Marca de clase: Es el punto medio de cada intervalo y es el valor que se utiliza para calcular otras medidas (realmente para el cálculo de frecuencias no es necesario este valor)
Vamos a ver un ejemplo de realizar una tabla de frecuencias con datos agrupados en intervalos:
Se toma una muestra de peces de una cierta especie y se miden sus longitudes en centímetros, cuyos resultados son:
Obtener la tabla de frecuencias absolutas, relativas y acumuladas.
La tabla de frecuencias tendrá las siguientes 5 columnas:
- Intervalos
- Frecuencia absoluta (fi)
- Frecuencia absoluta acumulada (Fi)
- Frecuencia relativa (ni)
- Frecuencia relativa acumulada (Ni)
Para rellenar la primera columna, tenemos que determinar el número de intervalos y la amplitud de los mismos. Para ello se identifica el valor más pequeño y el valor más grande, que en este caso son 5,42 y 8,42 respectivamente.
Ahora concretamos el número de intervalos que queremos y la amplitud para cada intervalo. Podemos hacerlo por ejemplo que con una amplitud de 0,5 y que empiecen desde 5 y lleguen hasta 8,5.
Nos quedan los siguientes intervalos:
Dejamos la última fila para el total.
Si queremos tener menos intervalos, sólo tenemos que ampliar la amplitud.
Para completar la columna de frecuencia absoluta, tenemos que ir contando los valores que pertenecen a cada intervalo.
Si por ejemplo tuviéramos el valor 5,5, pertenecería al segundo intervalo y no al primero, ya que el primer intervalo es abierto hasta 5,5, es decir, el 5,5 no está incluido y el segundo intervalo comienza a partir de 5,5, que sí está incluido, ya que el intervalo es cerrado por la izquierda.
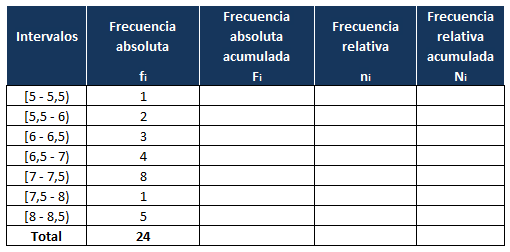
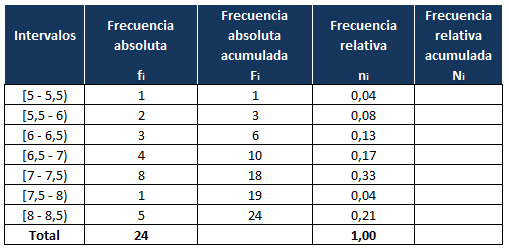
Después de contar nos queda de la siguiente manera:
Para completar la columna de la frecuencia absoluta acumulada de cada intervalo lo hacemos igual que en el caso anterior:en la primera fila, la frecuencia absoluta acumulada coincide con la frecuencia absoluta y para el resto de filas, la frecuencia absoluta acumulada la obtenemos sumando la frecuencia absoluta acumulada del dato anterior (del dato de arriba) más su frecuencia absoluta (dato de su izquierda).
Nos queda:
La frecuencia relativa la calculamos dividiendo cada frecuencia absoluta, entre el número total de elementos:
Por ejemplo, para el tercer intervalo, la frecuencia relativa es:
Lo hacemos igual para el resto de intervalos y en la última fila, colocamos la suma de las frecuencias relativas:
La frecuencia relativa acumulada del primer dato es igual que su frecuencia relativa y para los datos siguientes es igual a su frecuencia relativa más la frecuencia relativa del dato anterior (del dato de arriba):
O bien la podemos calcular la frecuencia relativa acumulada, dividiendo cada frecuencia absoluta acumulada entre el número de elementos total:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: