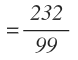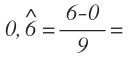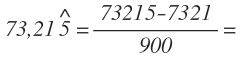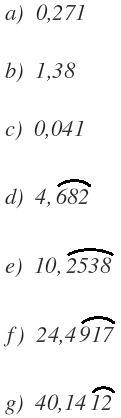A continuación te voy a explicar cómo pasar de decimal a fracción. Te lo explicaré paso a paso, para que lo entiendas todo y resolveremos algunos ejemplos y ejercicios paso a paso.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Para ponernos en situación vamos a ver los tipos de números decimales que existen:
Clasificación y tipos de números decimales
Existen dos tipos de números decimales: los números decimales exactos (o finitos) y los números decimales infinitos. Dentro de los números infinitos tenemos números decimales periódicos puros, los números decimales periódicos mixtos y los no periódicos.
Aquí te dejo un esquema para que lo visualices mejor.
Vamos a explicar ahora cada uno de ellos
Número decimal exacto
Los números decimales exactos son aquellos que tienen un número finito (que se acaba) de cifras decimales, como por ejemplo:
Número decimal periódico puro
Los números decimales periódicos puros son aquellos que tienen infinitas cifras decimales, donde se va repitiendo un patrón, formado por una o más cifras, al que se le llama periodo:
Se representa encerrando el periodo debajo de un arco, lo que indica que son esas cifras decimales las que se repiten continuamente.
Por ejemplo, en este caso el periodo es 26:
Y en este caso, el periodo es 478:
Como curiosidad, si quieres encontrar números decimales periódicos puros con periodos muy largos, sólo tienes que dividir cualquier número entre 7 (excepto los múltiplos de 7 claro)
Número decimal periódico mixto
Los números decimales periódicos mixtos son aquellos que tienen infinitas cifras decimales, donde también se va repitiendo un periodo, pero delante del periodo existen cifras decimales que no se repiten (llamado anteperiodo), como por ejemplo:
En este ejemplo, las dos primeras cifras decimales no se repiten (89) y luego tenemos el periodo que se repite infinitamente (126).
Número decimal infinito no periódico o irracionales
Los números decimales no periódicos o irracionales son aquellos que tienen infinitas cifras decimales, las cuales no se repiten siguiendo ningún patrón.
En este grupo de número decimales, se encuentran números muy conocidos en matemáticas, como el número π, el número e o el número de oro, además de las raíces que no son exactas:
Por ejemplo, son números decimales infinitos no periódicos el número pi, raíz de 2 o raíz de 3:
Una vez visto esto, vamos a ver ahora cómo podemos transformar los decimales a fracciones.
Los números decimales no periódicos son los únicos que no se pueden pasar a fracción. El resto te lo voy a ir explicando a continuación.
Aquí tienes un vídeo en el que resuelvo algunos ejercicios sobre pasar de decimal a fracción:
La explicación la tienes a continuación:
Cómo pasar un número decimal exacto a fracción
Para pasar un número decimal exacto a fracción, se escribe en el numerador el número decimal sin coma y en el denominador una potencia de 10, con tantos ceros como cifras decimales tenga el número.
Por ejemplo, si queremos pasar a decimal el número 0,75, en el numerador pondremos 75, que es el número decimal sin la coma (quedaría 075, pero el 0 a la izquierda desaparece porque no tiene valor). En el denominador podremos un 100, es decir una potencia de 10 con 2 ceros, ya que el número decimal tiene 2 cifras:
Después simplificamos la fracción:
Vamos a ver otro ejemplo:
En este caso el numerador corresponde a 3214, que es lo que queda al quitar la coma y en el denominador ponemos un 1000, es decir, una potencia de 10 con 3 ceros, ya que el número tiene 3 cifras decimales.
Una vez pasado a fracción simplificamos y queda:
Cómo pasar un número decimal periódico puro a fracción
Para pasar un número decimal periódico puro a fracción, en el numerador se escribe primero el número sin coma y se le resta la parte entera del número decimal. En el denominador, se escriben tantos 9 como cifras tenga el periodo.
Por ejemplo:
En el numerador, el número sin coma sería 234, al que le restamos la parte entera, es decir, la que está a la izquierda de la coma, que en este caso es un 2. En el denominador, ponemos un 99, es decir, un número con 2 nueves, ya que el periodo tiene 2 cifras.
Una vez hecho esto, realizamos la resta en el numerador y si se puede se simplifica la fracción, que en este caso no se puede simplificar:
Vamos a ver otro ejemplo:
En este caso, para el numerador, el número sin coma corresponde a un 6, que le restamos la parte entera que es un 0. Para el denominador, como sólo tenemos una cifra en el periodo, entonces será un 9.
Después operamos en el numerador y simplificamos la fracción:
Cómo pasar 0,9 periódico a fracción
Vamos a ver cómo pasar el 0,9 periódico a fracción. Verás que es algo bastante curioso.
En el numerador, escribimos el número sin coma que corresponde a un 9, y le restamos la parte entera que es un 0. En el denominador, como sólo tenemos una cifra en el periodo, escribimos un 9:
Y ahora operamos:
¿Qué ha pasado?
No hemos obtenido ninguna fracción, sino que hemos obtenido 1 como resultado.
Esto es porque en matemáticas el 0,999 es el número decimal periódico que es igual a 1:
Cómo pasar un número decimal periódico mixto a fracción
Para pasar un número decimal periódico mixto a fracción, en el numerador, se escribe primero el número decimal sin coma y se le resta la parte que está fuera del periodo, también sin coma, es decir la parte entera unida a los decimales que se quedan fuera del periodo.
El número del denominador estará formado por tantos 9 como cifras tenga el periodo, seguido de tantos 0 como cifras decimales haya fuera del periodo.
Por ejemplo:
En el numerador, el número sin coma sería 73215, al que le restamos la parte que queda fuera del periodo, sin coma, que en este caso es un 7321.
En el denominador, como tenemos una cifra dentro del periodo primero ponemos un 9, seguido de 2 ceros, que corresponde a las 2 cifras decimales que quedan fuera el periodo.
Después operamos en el numerador y simplificamos la fracción:
Vamos a ver otro ejemplo para que te quede más claro:
Para el numerador, el número sin coma es 61 y le restamos la parte que queda fuera del periodo, que en este caso es un 6. En el denominador, ponemos primero un 9, ya que dentro del periodo hay una cifra y un 0, ya que tenemos una cifra decimal fuera del periodo.
Para terminar, se realiza la resta en el numerador y después se simplifica:
Puedes comprobar si has pasado bien el número decimal a fracción tan sólo volviendo a realizar la división con la calculadora y viendo que el número decimal coincide.
Si quieres seguir aprendiendo a realizar operaciones con fracciones te recomiendo el Curso de Fracciones, con muchos ejercicios resueltos y propuestos para practicar.
Convertir decimales a fracciones. Ejercicios
Ejercicio 1
Pasar a fracción los siguientes números decimales:
Ejercicio 2
Resuelve la siguiente operación:
Tienes la solución en el vídeo de más arriba.
Ejercicio 1
Aquí tienes los resultados, que son los mismos que los del vídeo de más arriba:
Ejercicio 2
En primer lugar pasamos los números decimales a fracción:
Realizamos las restas de los denominadores:
Realizamos la multiplicación y división de fracciones. Lo dejamos indicado sin llegar a multiplicar los números con el objetivo de poder simplificar después:
Descomponemos los factores para poder simplificar:
Eliminamos los factores que se repiten en el numerador y el denominador:
Nos queda:
Realizamos la multiplicación en el numerador:
Para poder sumar o restar fracciones, necesitamos obtener el denominador común.
Para ello descomponemos los factores:
Y obtenemos su mínimo común múltiplo:
Reducimos las fracciones a común denominador:
Operamos y simplificamos:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: