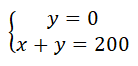Vamos a ver cómo resolver problemas de programación lineal. Te explicaré cuál es el procedimiento a seguir y lo aplicaremos en problemas resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolver algún ejercicio que se te resista o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Procedimiento para resolver problemas de programación lineal
Los problemas de programación lineal son problemas en los que hay que optimizar, es decir, maximizar o minimizar, una función lineal, llamada función objetivo, que depende de varias variables, que están sujetas a una serie de restricciones expresadas por inecuaciones lineales.
El procedimiento para resolver los problemas de programación lineal es el siguiente:
- Asignar las incógnitas: Estas incógnitas corresponderán a lo que el problema nos esté preguntando para optimizar su resultado
- Definir la función objetivo: Será una función lineal que dependerá de dos variables, x e y. Es la función que tendremos que maximizar o minimizar. Tiene la siguiente forma:
- Determinar las restricciones sujetas a la función objetivo: El enunciado nos indicará una serie de restricciones que se combinan con las variables de la función, junto con un valor límite para cada una. Tendremos que expresar cada restricción como una inecuación lineal. Nos ayudaremos de una tabla para ordenar la información.
- Obtener la región factible: La región factible es el recinto donde se cumplen todas las restricciones del problema, es decir, es la solución del sistema de inecuaciones. Se obtiene representando cada una de las inecuaciones lineales. los puntos que pertenecen a la región factible se llaman soluciones factibles y entre todas las soluciones, se encuentra la solución óptima (la máxima o la mínima) que coincidirá con uno de los vértices de la región factible.
- Hallar las coordenadas de los vértices de la región factible: Para ello, hay que resolver el sistema de ecuaciones que forman las dos rectas del vértice.
- Obtener los valores de la función objetivo con los valores de las coordenadas de cada uno de los vértices, para encontrar la solución óptima.
Consideraciones a tener en cuenta:
- En algunos problemas de programación lineal, se indican restricciones que no aportan información para obtener la solución, es decir, que no las necesitamos para definir la región factible. A estas restricciones se denominan restricciones redundantes.
- La región factible puede estar acotada (recinto cerrado) o no acotada (recinto abierto). Si la región factible está acotada, el problema tendrá una solución óptima. Si no está acotada, puede que tenga infinitas soluciones o ninguna solución.
Ahora, vamos a aplicar este procedimiento resolviendo algunos problemas de programación lineal paso a paso.
Problemas de programación lineal resueltos paso a paso
Problema 1
Con el fin de sufragar los gastos del viaje de estudios de año Trece, los alumnos de un instituto organizan la venta de bombones y mantecados. Disponen de 600 cajas de bombones y 1000 cajas de mantecados, que van a distribuir en dos tipo de lotes, A y B. Cada lote A consta de 2 cajas de bombones y 1 caja de mantecados. Cada lote B contiene 1 caja de bombones y 3 cajas de mantecados. Si el beneficio obtenido por un lote A es de 10 € y por un lote B es de 12 € se pide:
a) El número de lotes de cada tipo para obtener el máximo beneficio
b) El valor de dicho beneficio máximo
En primer lugar debemos asignar las incógnitas, que será lo que nos pregunte el problema para obtener los beneficios máximos. En este caso nos preguntan por el número de lotes, luego llamaremos x a la cantidad de lotes tipo A e «y» a la cantidad de lotes tipo B:
Una vez tenemos las incógnitas, definimos la función objetivo, que es la que nos determina el beneficio que queremos maximizar y depende de x y de «y». No dicen que el beneficio obtenido por un lote A es de 10 € y por un lote B es de 12 €, luego la función objetivo la obtenemos multiplicando el precio de cada lote por el número de cada lote:
Ahora vamos a determinar las restricciones que están sujetas a esta función. Para ello creamos una tabla donde en la que indicaremos el número de bombones y mantecados tiene cada lote, así como las unidades disponibles de cada uno de ellos.
En la primera fila colocamos los lotes de cada tipo, que es a los que les asignamos incógnita, así como las restricciones o las unidades disponibles. Después añadimos una fila para la cajas de bombones y otra para las cajas de mantecados. La tabla queda de esta forma:
Ahora vamos a ir rellenando la tabla. Nos dicen que cada lote A consta de 2 cajas de bombones y 1 caja de mantecados:
Y que disponen de 600 cajas de bombones:
Cada lote B contiene 1 caja de bombones y 3 cajas de mantecados:
Disponen de 1000 cajas de mantecados:
Ahora ya podemos determinar las restricciones de la función objetivo, que estarán dadas por inecuaciones lineales.
Por un lado, el número de lotes tipo A y tipo B, será mayor o igual que 0:
Luego, de la fila de las cajas de bombones, obtenemos que el número de cajas de bombones será igual a 2 por el número de lotes tipo A más el número de lotes tipo B y que eso no debe superar las 600 unidades, es decir, debe ser menor o igual a 600:
De la fila de las cajas de mantecados, obtenemos que el número de cajas de mantecados será igual al número de lotes tipo A más 3por el número de lotes tipo B y que eso debe ser menor o igual a 1000:
Tenemos por tanto un sistema de 4 inecuaciones lineales, que corresponden a las restricciones de la función objetivo.
El siguiente paso es representar cada una de las inecuaciones lineales (restricciones) para obtener la región factible, que es el recinto que determina la solución del sistema de inecuaciones y cuyos punto verifican todas las restricciones.
Representamos la primera restricción:
Representamos la segunda restricción:
La tercera restricción:
Y la cuarta restricción:
La región factible es la zona donde se cumplen todas las restricciones y queda determinada por los vértices A, B, C y D:
Ahora vamos a obtener las coordenadas de los vértices de la región factible, resolviendo el sistema formado por las rectas de corte de cada vértice.
El vértice A lo obtenemos resolviendo el sistema formado por las siguientes rectas:
Cuyo resultado es:
Vértice B:
Vértice C: 
El vértice D es el origen de coordenadas que es (0,0).
Por tanto, las coordenadas de cada vértice son:
Por último, hallamos los valores de la función objetivo (beneficios) para cada uno de los vértices, sustituyendo x e «y» por sus valores en cada vértice.
Para el vértice A:
Para el vértice B:
Para el vértice C:
La solución óptima, en la que los beneficios son máximos, corresponde al vértice B.
Así que, hay que vender 160 lotes tipo A y 280 lotes tipo B, siendo el beneficio máximo 4960 euros,
Problema 2
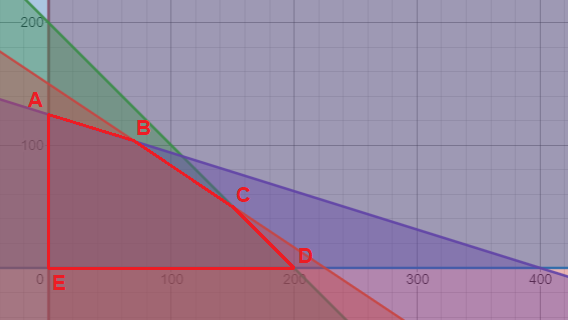
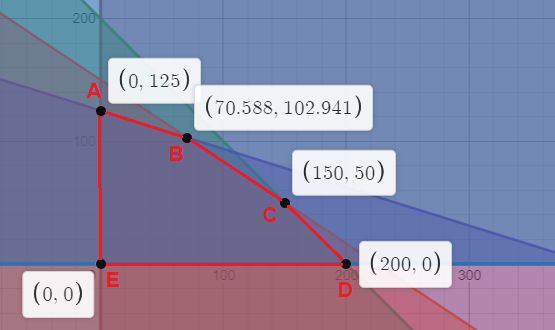
Se dispone de 200 hectáreas de terreno en las que se desea cultivar patatas y zanahorias. Cada hectárea dedicada al cultivo de patatas necesita 12,5 litros de agua de riego al mes, mientras que cada una de zanahorias necesita 40 litros, disponiéndose mensualmente de un total de 5000 litros de agua para el riego. Por otra parte, las necesidades por hectárea de abono nitrogenado son de 20 kg para las patatas y de 30 kg para las zanahorias, disponiéndose de un total de 4500 kg de abono nitrogenado. Si la ganancia por hectárea sembrada de patatas es de 300 € y de 400 € la ganancia por cada hectárea de zanahorias, ¿qué cantidad de hectáreas conviene dedicar a cada cultivo para maximizar la ganancia? ¿Cuál sería esta?
Empezamos asignando las incógnitas. El problema nos pregunta por la cantidad de hectáreas conviene dedicar a cada cultivo para maximizar la ganancia, por tanto, llamaremos x a las hectáreas dedicadas a las patatas e «y» a las hectáreas dedicadas a las zanahorias:
Ahora definimos la función objetivo. La ganancia por cada hectárea sembrada de patatas es de 300 € y la de cada hectárea de zanahorias es de 400 €, así que la función objetivo nos queda:
Seguimos con las restricciones sujetas a la función. Creamos una tabla con las hectáreas para las patatas (x) en una columna, las hectáreas para las zanahorias (y) en otra columna y las restricciones o cantidad disponible en otra. Añadimos una fila para el agua y otra para el abono:
Nos dicen que cada hectárea dedicada al cultivo de patatas necesita 12,5 litros de agua de riego al mes, mientras que cada una de zanahorias necesita 40 litros:
Se dispone mensualmente de un total de 5000 litros de agua para el riego:
Las necesidades por hectárea de abono nitrogenado son de 20 kg para las patatas y de 30 kg para las zanahorias:
Se dispone de un total de 4500 kg de abono:
Empezamos a determinar las restricciones que están sujetas a la función objetivo.
Con respecto a las hectáreas, tanto las dedicadas a las patatas (x) como las dedicadas a las zanahorias (y), serán mayores o iguales que 0:
Además, el enunciado del problema nos dice que se dispone de 200 hectáreas de terreno, luego la suma de todas las hectáreas no puede superar esa cantidad:
De la tabla obtenemos que el agua utilizada en cada tipo de hectárea, es decir, 12,5 litros por las hectáreas de patatas, más 40 litros por las hectáreas de zanahorias, debe ser menor que 5000 litros:
De la misma forma, de la última fila de la tabla obtenemos que el abono utilizado en cada tipo de hectárea, es decir, 20 kg por las hectáreas de patatas, más 30 kg por las hectáreas de zanahorias, no puede superar los 4500 kg:
Vamos a representar cada una de las 5 restricciones anteriores para obtener la región factible.
Primera restricción:
Segunda restricción:
Tercera restricción:
Cuarta restricción:
Y quinta restricción:
La región factible donde se cumplen todas las restricciones queda determinada por los vértices A, B, C, D y E:
Vamos a calcular las coordenadas de los vértices de la región factible, resolviendo el sistema formado por las rectas de corte de cada vértice.
Vértice A:
Vértice B:
Vértice C:
Vértice D:
El vértice E es el origen de coordenadas que es (0,0).
Las coordenadas de cada vértice son:
Por último, vamos a hallar los valores de la función objetivo (beneficios) para cada uno de los vértices, sustituyendo x e «y» por los valores de cada vértice.
Para el vértice A:
Para el vértice B:
Para el vértice C:
Para el vértice D:
Así que, la solución óptima, donde los beneficios son máximos es el vértice C, por lo que habría que cultivar 150 hectáreas de patatas y 50 hectáreas de zanahorias, siendo el beneficio máximo de 65000 €.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: