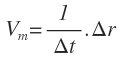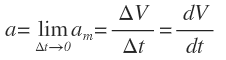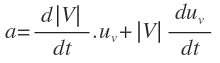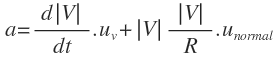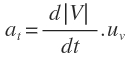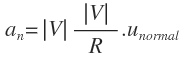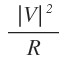A continuación voy a explicarte lo que necesitas saber para conocer la teoría y cómo se obtienen las fórmulas de la velocidad y el concepto aceleración y su fórmula con vectores.
Te explicaré las fórmulas tanto de la velocidad media y la velocidad instantánea, como de la aceleración media y la aceleración instantánea.
Además veremos cuáles son los componentes por los que está formada la aceleración.
Si has llegado hasta aquí es porque buscas ayuda para resolver algún problema de física y necesitas clases de física online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Física Online:
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y física. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus problemas de física
¿Qué es el movimiento?
Vamos a empezar definiendo el movimiento, concepto que nos ayudará a entender todo lo demás.
Si cuando viajamos de acompañante en una moto, nos preguntáramos si nos estamos moviendo, la respuesta a lo mejor no está tan clara.
Por un lado observamos que, efectivamente, que los árboles situados a ambos lados de la carretera vienen hacia nosotros, con lo que la respuesta sería que sí me muevo.
Por otro lado, mi distancia con el conductor de la moto permanece constante y por tanto, tendría que decir que no me estoy moviendo.
La solución a esta paradoja está en considerar que el movimiento es el cambio de posición con respecto a una referencia.
Si como referencia tomo un árbol de la carretera, sí me estoy moviendo. Si tomo como referencia al conductor de la moto no me estoy moviendo.
Con esta definición, es sencillo entender la frase el movimiento es siempre relativo, ya que se necesita relacionar la posición de un objeto con una posición de referencia elegida.
Para establecer, sin ninguna duda, si un cuerpo se mueve o no, es imprescindible que no se mueva absolutamente nada.
Durante muchísimos años, se creyó que las estrellas lejanas estaban completamente inmóviles en el firmamento y que por tanto, se podrían utilizar para indicar con absoluta confianza si un cuerpo estaba moviéndose en reposo absoluto.
Sin embargo, hoy sabemos que no existe nada en el universo que esté en reposo absoluto.
No podemos hablar, por lo tanto, de movimiento o reposo absolutos.
Posición de un cuerpo con respecto a una referencia
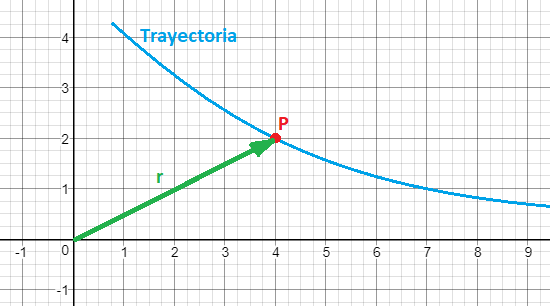
Llamamos trayectoria a la línea (curva o recta) que sigue un cuerpo durante su movimiento.
La posición de un cuerpo se determina mediante un vector r, conocido como vector de posición, que tiene como origen la referencia elegida y como extremo el lugar donde se encuentra el cuerpo.
Así en la imagen, se puede decir que la posición del cuerpo P, con respecto al punto O (0,0) viene dada por el vector de posición r:
Desplazamiento
Como el móvil se mueve a lo largo de su trayectoria, vamos a definir una nueva magnitud para determinar los cambios de posición.
Esta nueva magnitud es el vector desplazamiento, que se define como la diferencia entre dos vectores de posición final e inicial:
A partir de ahora vamos a referirnos al vector desplazamiento como:
El operador Δ (incremento), indica la operación de restarle el valor inicial al valor final de una determinada magnitud.
Velocidad media y velocidad instantánea
Todos los cambios de posición se realizan en un cierto intervalo de tiempo.
Velocidad media
Para distinguir entre dos móviles que realizan el mismo desplazamiento, pero en distinto tiempo se introduce una magnitud, que tiene en cuenta el tiempo que tarda el móvil en realizar su trayectoria. Hablamos de la velocidad media.
Se define la velocidad media de un cuerpo como el cociente entre su desplazamiento y el tiempo que tarda en recorrerlo:
La velocidad media es una magnitud vectorial.
Cuando se multiplica un vector por un número, el módulo del vector queda multiplicado por ese número, manteniendo dirección y sentido.
Este es el mismo caso. El denominador de esta ecuación es un número, por lo que la velocidad media es igual a un número por el vector desplazamiento:
En consecuencia, la velocidad media tiene la misma dirección y sentido que el vector desplazamiento y su módulo es igual al módulo del vector desplazamiento dividido entre el intervalo de tiempo:
Al módulo de la velocidad media se le puede llamar también celeridad media o rapidez media.
Por tanto, para que te quede más claro, ¿cuál es la diferencia entre velocidad y rapidez?
Pues que la velocidad es una magnitud vectorial y la rapidez es el módulo de la velocidad y es una magnitud escalar.
Velocidad instantánea
Se denomina velocidad instantánea o simplemente velocidad, a la velocidad media de un móvil cuando el intervalo de tiempo de ir de un punto a otro es muy pequeño, tan pequeño que el tiempo tiende a ser cero:
El operador d, indica que el incremento es muy pequeño.
La velocidad también tiene la misma dirección y sentido que el vector desplazamiento.
Como los intervalos de tiempo son muy pequeños el punto final de cada intervalo está muy próximo al punto de partida y eso significa que:
1. El módulo del vector desplazamiento dr, coincide con el espacio recorrido por el móvil: Esto no ocurriría cuando el intervalo de tiempo era grande. Observa esta imagen:
El móvil que sale del punto P, al cabo de un cierto intervalo de tiempo, llega al punto Q.
El módulo del vector desplazamiento mide menos que el espacio recorrido por el cuerpo. Si vamos disminuyendo el tiempo, es decir, que el móvil va retrocediendo, nos fijamos que el móvil ha pasado antes por R, antes por S, antes porque T, antes por U y así sucesivamente para cada uno de los puntos.
La diferencia entre lo que mide la curva y lo que mide el vector desplazamiento va disminuyendo. En el límite, cuando el intervalo de tiempo se aproxima muchísimo a cero, esa diferencia es nula.
2. El vector desplazamiento y el vector velocidad, son en cada punto tangente a la trayectoria.
3. Su módulo es igual al módulo del vector desplazamiento dividido entre el intervalo de tiempo:
Al módulo de la velocidad se le llama también celeridad o rapidez
Aceleración media y aceleración instantánea
La aceleración es una magnitud que nos informa si la velocidad de un móvil varía con el tiempo.
Fórmula de la aceleración media
Sea un móvil que en un cierto intervalo de tiempo, se mueve del punto 1 al punto 2:
En cada punto, lleva unas velocidades V1 y V2, que son diferentes en módulo y dirección.
La fórmula de la aceleración media es igual al vector variación de velocidad entre un intervalo de tiempo:
La aceleración media también es una magnitud vectorial.
Como antes se ha mencionado para la velocidad media la aceleración media tiene la misma dirección y sentido que el vector velocidad y su módulo es igual al módulo del vector velocidad dividido entre el intervalo tiempo:
Fórmula de la aceleración instantánea
Se denomina aceleración instantánea simplemente aceleración, a la aceleración de un móvil cuando se considera un intervalo de tiempo tan pequeño que tiende a cero.
La fórmula de la aceleración instantánea es:
Sin embargo, la aceleración instantánea no se suele calcular, ya que suele ser un dato del problema. Es decir, es la aceleración que tiene un determinado objeto o cuerpo en un instante dado.
La aceleración tiene la misma dirección y sentido que la variación de la velocidad dv y su módulo es igual al módulo de la variación de velocidad entre el intervalo de tiempo:
Aceleración normal y tangencial. Fórmulas
La velocidad es un vector que puede variar si cambia su módulo o su dirección. En cualquiera de los dos casos tiene que existir una aceleración.
De la definición de aceleración:
podemos sustituir el vector velocidad y su módulo y vector unitario:
Si derivamos un producto, el resultado es la suma de la derivada del primero, por el segundo sin derivar, más el primero sin derivar más la derivada del segundo:
Vamos a examinar ambos sumandos del segundo miembro.
El primero se refiere a como varía el módulo de la velocidad con el tiempo. Su dirección es la misma que la del vector velocidad, ya que posee su mismo de vector unitario.
A ese sumando se le conoce como aceleración tangencial, ya que igual que la velocidad, es tangente a la trayectoria.
El segundo sumando indica como varía con el tiempo la dirección de la velocidad.
Se puede demostrar que la variación del vector unitario de la velocidad con el tiempo, es otro vector perpendicular a él y cuyo módulo es:
siendo R el radio del arco de la trayectoria en ese punto:
Sustituyendo en la ecuación de la aceleración tendremos:
Como te comenté anteriormente, el primer sumando del segundo miembro es la aceleración tangencial:
Al segundo sumando se le denomina aceleración normal o centrípeta:
Cuyo módulo viene expresado por:
Para resumir, la celebración tiene dos componentes intrínsecas:
- La aceleración tangencial, que la poseen todos los móviles, cuya rapidez varía tiempo
- La aceleración normal, que la tienen aquellas móviles en los que la velocidad cambia de dirección con el tiempo, o en otras palabras, se mueven en trayectorias curvas.
El vector aceleración está relacionado con sus componentes de la siguiente manera:
Y sus módulos se relacionan mediante la siguiente ecuación:
¿Necesitas ayuda en física y matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar.
He diseñado un método práctico y efectivo que te ayudará a entender la física así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos problemas y saber aplicar las fórmulas que correspondan. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus problemas de física
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender física y matemáticas? Pulsa el botón para saber más: