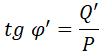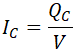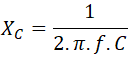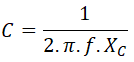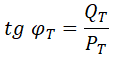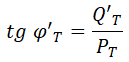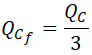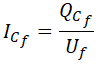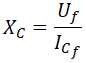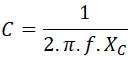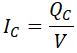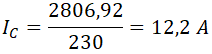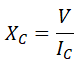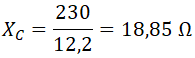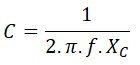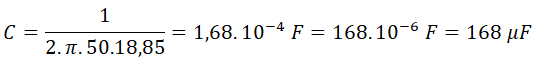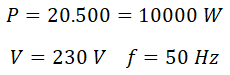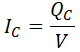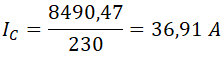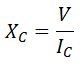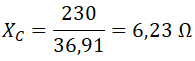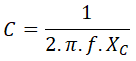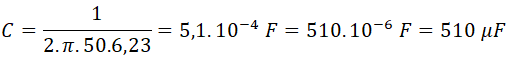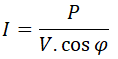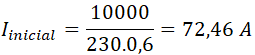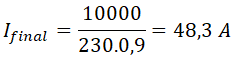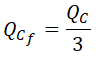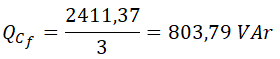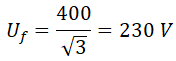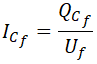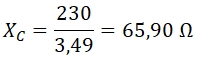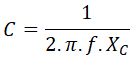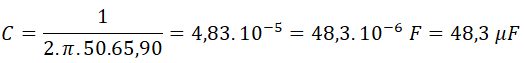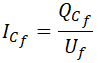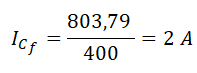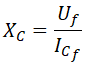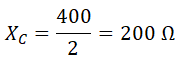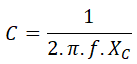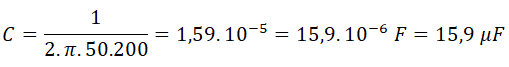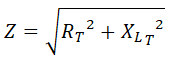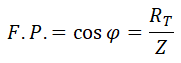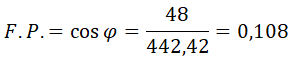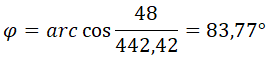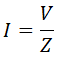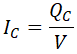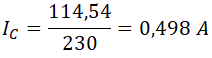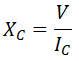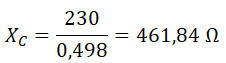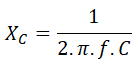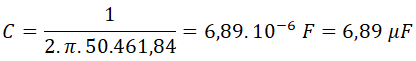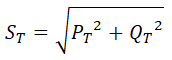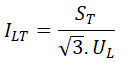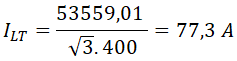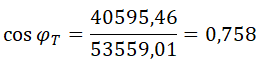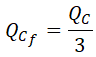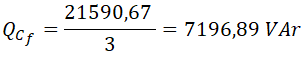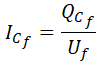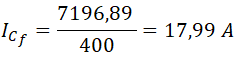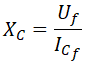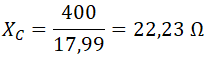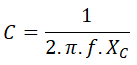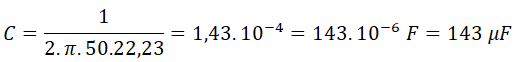Corrección del factor de potencia en circuitos monofásicos y trifásicos. Ejercicios

Vamos a ver cómo corregir el factor de potencia en circuitos monofásicos y trifásicos en corriente alterna, con el fin de aproximarlo lo máximo posible a la unidad al reducir la potencia reactiva de la instalación. Con ejercicios resueltos paso a paso.

¡Empezamos!

Si has llegado hasta aquí es porque hay algún ejercicio que no sabes resolver y necesitas clases de electrotecnia online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Electrotecnia Online:

VER CURSOS DE ELECTROTECNIA ONLINE

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y electrotecnia. Puedo explicarte paso a paso cualquier duda que no entiendas.

Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de electrotecnia.

Importancia de corregir el factor de potencia

Cuando un el factor de potencia está muy lejos de ser igual a la unidad se debe a una potencia reactiva elevada, causada por el efecto de la inducción de los bobinados.

La potencia reactiva no se transforma en trabajo útil, sino que únicamente sirve para generar el campo magnético y es devuelta al generador, por lo que la línea absorbe de la red eléctrica una potencia aparente muy superior a la que realmente se consume.

Como consecuencia, se produce un aumento de intensidad por los conductores que repercute directamente en el coste de consumo eléctrico.

La corrección del factor de potencia se lleva a cabo mediante condensadores, en el caso de circuitos monofásicos o en el caso de circuitos trifásicos mediante baterías de condensadores trifásicos, conectados en estrella o en triángulo dentro de una misma envolvente, que se conectan en paralelo a los receptores de la instalación, al principio de la línea.

Estas baterías de condensadores compensan parte de la potencia reactiva creada por las bobinas de la instalación.

Beneficios de corregir el factor de potencia

Cuando corregimos el factor de potencia y lo acercamos lo máximo posible a la unidad, se obtiene una disminución de la intensidad, así como de la potencia reactiva y como consecuencia de la potencia aparente.

Por otro lado, las compañías eléctricas no facturan la potencia reactiva, pero sin embargo exigen que los consumidores trabajen con un factor de potencia cercano a 1 (aproximadamente en 0,95) y para ello disponen de equipos de medida para determinar el factor de potencia medio utilizado durante el periodo de facturación.

Como la energía reactiva no se cobra, lo que se hace es aplicar un recargo en el precio de la energía consumida a los clientes que trabajen con un factor de potencia por debajo del recomendado.

En resumen, con la mejora del factor de potencia se consigue reducir la potencia aparente de la instalación, sin modificar la potencia activa, lo que conlleva una reducción de la intensidad consumida, lo que aporta ciertas ventajas, como la reducción de la sección en los conductores, reducción de la caída de tensión y reducción de la pérdida de potencia.

Corrección del factor de potencia mediante condensadores en paralelo en circuitos monofásicos

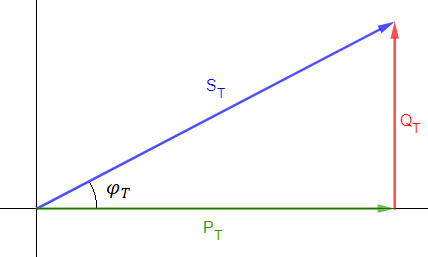
Partimos de la base de que tenemos un circuito con una potencia reactiva inductiva, al que queremos corregir el factor de potencia, cuyo triángulo de potencias es el siguiente:

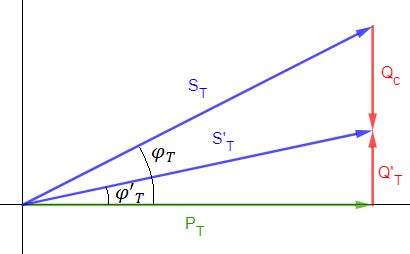
Para corregir el factor de potencia, instalamos en paralelo un condensador, lo que provoca que a la potencia reactiva total inicial (inductiva), se le resta la potencia reactiva del condensador, ya que al ser una potencia reactiva capacitiva, va en sentido contrario a la inductiva, obteniendo una potencia reactiva Q’ menor que la inicial:

Nos queda entonces un nuevo triángulo de potencias, donde ahora la potencia reactiva total es Q’ y por tanto, se ven modificadas la potencia aparente, que pasa a ser S’, el ángulo de desfase, que pasa a ser φ’, modificándose el factor de potencia, que es lo que queremos conseguir:

Cómo calcular la potencia reactiva capacitiva del condensador en circuitos monofásicos

Como hemos comentado antes, la nueva potencia reactiva del circuito Q’ es igual a la potencia reactiva antigua Q menos la potencia reactiva del condensador:

De esta expresión, podemos despejar la potencia reactiva del condensador:

Por otro lado, aplicando trigonometría al triángulo de potencias inicial (sin el factor de potencia corregido)tenemos:

De donde podemos despejar la potencia reactiva inicial:

Hacemos lo mismo en el triángulo de potencias final, es decir, después de corregir el factor de potencia:

Y despejamos la potencia reactiva final:

Ahora, en la expresión donde teníamos despejada la potencia reactiva del condensador:

Sustituimos las potencias reactivas inicial y final por las expresiones obtenidas por trigonometría:

Y por último, sacamos factor común a la potencia activa, quedándonos una fórmula para calcular la potencia reactiva del condensador en función de la potencia activa y los ángulos de desfase inicial y final:

Esta fórmula la puedes utilizar directamente para resolver tus ejercicios.

Cómo calcular la capacidad del condensador

Una vez conocida la potencia reactiva del condensador, podemos calcular la capacidad del condensador.

Como el condensador es puramente capacitivo, se cumple que su potencia reactiva es igual a la tensión aplicada al condensador, por la intensidad que circula por él:

De donde podemos despejar la intensidad que circula por el condensador:

Aplicando la ley de Ohm al condensador, tenemos que la reactancia capacitiva es igual a la tensión entre la intensidad:

Por otro lado, la fórmula de la reactancia capacitiva del condensador es:

de donde despejamos la capacidad del condensador:

Corrección del factor de potencia mediante baterías de condensadores en sistemas trifásicos

Tenemos una instalación a la que queremos corregir el factor de potencia, cuyo triángulo de potencias es el siguiente:

Cuando instalamos una batería de condensadores en la línea general de alimentación de la instalación, a la potencia reactiva total inicial (inductiva), se le resta la potencia reactiva de la batería de condensadores, ya que al ser una potencia reactiva capacitiva, va en sentido contrario a la inductiva, obteniendo una potencia reactiva Q’t reducida:

Nos queda por tanto un nuevo triángulo de potencias, donde ahora la potencia reactiva total es Q’t y por tanto, se ven modificadas la potencia aparente, que pasa a ser S’t, el ángulo de desfase, que pasa a ser φ’t y por tanto, también se modifica el factor de potencia, que es lo que buscamos.

Cómo calcular la potencia reactiva capacitiva de la batería de condensadores en sistemas trifásicos

De la expresión anterior, podemos despejar la potencia reactiva del condensador, que es igual a la potencia reactiva inicial menos la potencia reactiva final:

Por otro lado, aplicando trigonometría al triángulo de potencias inicial tenemos:

De donde done podemos despejar la potencia reactiva inicial:

Hacemos lo mismo en el triángulo de potencias final:

Y despejamos la potencia reactiva final:

Ahora, en la expresión donde despejamos la potencia reactiva del condensador:

Sustituimos las potencias reactivas inicial y final por las expresiones obtenidas por trigonometría:

Sacamos factor común a la potencia activa y nos queda:

Nos queda una fórmula para calcular la potencia reactiva de la batería de condensadores en función de la potencia activa y los ángulos de desfase inicial y final.

Cómo calcular la capacidad del condensador

Una vez conocida la potencia reactiva de la batería de condensadores, podemos calcular la capacidad del condensador por cada una de las fases de la batería de condensadores.

La potencia de cada una de las fases de la batería de condensadores será la tercera parte de la potencia reactiva total de la batería de condensadores:

Por otro lado, sabemos que la potencia reactiva en cada fase es igual a la tensión de fase por la intensidad de fase:

Expresión de la que podemos despejar la intensidad por fase de la batería de condensadores:

Aplicando la ley de Ohm a cada fase, tenemos que la reactancia capacitiva por fase es igual a la tensión de fase entre la intensidad de fase, valor que podemos calcular porque conocemos la tensión y la intensidad por fase:

Una vez calculada la reactancia capacitiva, podemos calcular la capacidad del condensador por fase con la siguiente fórmula:

Ejemplos de cálculo de condensadores y batería de condensadores para corregir el factor de potencia

Circuitos monofásicos

Ejemplo 1

Calcular las características del condensador que hay que conectar en paralelo a un motor monofásico de 2000 W, 230 V y 50 Hz con un factor de potencia de 0,5 para conseguir corregirlo hasta 0,95.

Tenemos un motor con las siguientes características:

cuyo factor de potencia es:

Calculamos el ángulo de desfase con la inversa del coseno:

Nos piden corregir el factor de potencia a 0,95:

que corresponde al siguiente ángulo de desfase:

Calculamos la potencia reactiva del condensador aplicando directamente la fórmula que depende de la potencia activa y los ángulos de desfase inicial y final:

Sustituimos valores y operamos:

La potencia reactiva del condensador es igual a:

de donde podemos despejar la intensidad de condensador:

Sustituimos valores y operamos:

Conocidas la tensión y la intensidad por el condensador, podemos calcular la reactancia capacitiva, aplicando la ley de ohm:

Con el valor de la reactancia capacitiva, ya podemos calcular la capacidad del condensador aplicando la siguiente fórmula:

Sustituimos valores y operamos:

Necesitamos un condensador de 168 μF a 230 V y 3 kVAr.

Ejemplo 2

El alumbrado de una nave industrial consiste en 20 lámparas de vapor de mercurio de 500 W cada una con un factor de potencia de 0,6 a 230 V y 50 Hz. Averiguar las características del condensador para conseguir elevar el factor de potencia de la instalación hasta 0,9, así como la intensidad de corriente de la instalación antes y después de la corrección del factor de potencia.

Las características de la instalación son:

Al ser el factor de potencia el mismo en todas las lámparas, el factor de potencia de la instalación es también 0,6:

que corresponde al siguiente ángulo de desfase:

Nos piden corregir el factor de potencia a 0,9:

cuyo ángulo de desfase es:

Calculamos la potencia reactiva del condensador con la siguiente fórmula:

Sustituimos valores y operamos:

Por otro lado, la potencia reactiva del condensador es igual a:

de donde despejamos la intensidad del condensador y la calculamos:

Calculamos la reactancia capacitiva, aplicando la ley de ohm:

Y finalmente, calculamos la capacidad del condensador a instalar en paralelo:

Necesitamos un condensador de 510 μF a 230 V y 8,5 kVAr.

Ahora vamos a calcular la intensidad antes y después de corregir el factor de potencia.

Sabemos que la fórmula para calcular la potencia activa es:

de donde podemos despejar la intensidad, ya que conocemos la potencia de la instalación, la tensión y el factor de potencia antes y después:

Para calcular la intensidad antes de corregir el factor de potencia sustituimos el coseno de φ por 0,6:

Y para calcular la intensidad después de corregir el factor de potencia sustituimos el coseno de φ por 0,9:

Como ves, uno de los beneficios de corregir el factor de potencia es reducir el consumo de la instalación.

Sistemas trifásicos

Vamos a ver con unos ejemplos resueltos, cómo calcular la batería de condensadores trifásica en una instalación trifásica, aplicando lo que hemos visto hasta ahora. Dependiendo de cómo se conecten las baterías (en estrella o en triángulo) cambiarán algunas de sus características.

Ejemplo 1

Una instalación se compone de 60 lámparas fluorescentes de 40 W, 230 V y un factor de potencia de 0,6. Las lámparas se han conectado de forma equilibrada a una red trifásica de 400 V y 50 Hz. Calcular la batería de condensadores en estrella que será necesario instalar en la línea general de alimentación para corregir el factor de potencia a 0,95.

Calculamos la potencia activa total de la instalación multiplicando el número de lámparas por la potencia unitaria de cada lámpara:

Las lámparas tienen un factor de potencia de 0,6:

A partir de la fórmula inversa del coseno, calculamos el ángulo de desfase de la instalación:

Queremos corregir el factor de potencia a 0,95:

Lo que corresponde a un nuevo ángulo de desfase:

Ya tenemos todos los datos para calcular la potencia del condensador con la siguiente fórmula (que hemos deducido más arriba):

Sustituimos valores y operamos:

La batería de condensadores a instalar en la línea de alimentación de la instalación debe tener una potencia reactiva de 2411,37 VAr.

Ahora vamos a calcular la capacidad de cada uno de los condensadores que forma la batería de condensadores.

Para ello, calculamos la potencia reactiva por fase dividiendo la potencia reactiva total entre 3:

La tensión de línea en una conexión en estrella es igual a raíz de tres veces la tensión de fase:

De donde despejamos la tensión de fase:

La potencia reactiva por fase es igual a la tensión de fase por la intensidad de fase:

De donde podemos despejar la intensidad que circula por cada fase de la batería de condensadores:

Sustituimos valores y operamos:

En cada fase, la reactancia capacitiva es igual a la tensión de fase entre la intensidad de fase:

Sustituimos valores y operamos:

Y finalmente calculamos la capacidad del condensador de cada fase:

Por tanto, la batería de condensadores a instalar deberá tener una potencia de 2411,37 VAr a 400 V y está formada por 3 condensadores de 48,3 μF a 230 V conectados en estrella.

Ejemplo 2

En la instalación del ejemplo anterior, calcular la batería de condensadores en triángulo que será necesario instalar en la línea general de alimentación para corregir el factor de potencia a 0,95.

En este caso, la potencia reactiva de la batería de condensadores será exactamente la misma que en el caso anterior:

Lo que sí será diferente es la tensión a la que trabaja la batería de condensadores así como la intensidad que circula por cada fase, por lo que se verá afectada la capacidad de los condensadores.

En una conexión en triángulo, la tensión de línea es igual a la tensión de fase:

Por lo que la tensión en caca fase de la batería de condensadores es:

La potencia reactiva por fase es igual a la tensión de fase por la intensidad de fase:

De donde podemos despejar la intensidad que circula por cada fase de la batería de condensadores, que en este caso es:

En cada fase, la reactancia capacitiva es igual a la tensión de fase entre la intensidad de fase:

Que sustituyendo valores y operando nos queda:

Por último calculamos la capacidad del condensador de cada fase:

Por tanto, la batería de condensadores a instalar deberá tener una potencia de 2411,37 VAr a 400 V y está formada por 3 condensadores de 15,9 μF a 400 V conectados en triángulo.

Cuando la conexión de la batería de condensadores es en triángulo, se consiguen condensadores de menor capacidad, pero de mayor tensión nominal que con una batería en estrella.

Ejercicios resueltos de corrección del factor de potencia en circuitos monofásicos y en sistemas trifásicos con varios receptores

Ejercicio resuelto en circuitos monofásicos

Se conectan en serie las bobinas de dos contactores a 230 V, 50 Hz de las siguientes características:

• Bobina número 1: R= 20 Ω y L=0,8 H
• Bobina número 2: R= 28 Ω y L=0,6 H

Calcula la corriente que fluye por las bobinas, la tensión aplicada a cada una, el factor de potencia del conjunto, las potencias del conjunto y la capacidad del condensador que habrá que conectar en paralelo para conseguir corregir el factor de potencia del conjunto a 0,95.

En primer lugar calculamos la resistencia total equivalente del circuito sumando las resistencias:

Por otro lado, calculamos las reactancias inductivas de cada bobina con la fórmula:

Para calcular la reactancia inductiva de la bobina número 1, sustituimos L por su valor y operamos:

Hacemos lo mismo para la reactancia inductiva de la bobina número 2:

Calculamos la reactancia inductiva total equivalente del circuito sumando ambas reactancias:

Una vez tenemos la resistencia y la reactancia total, obtenemos la impedancia equivalente del circuito:

Una vez obtenida la impedancia, podemos calcular el factor de potencia:

Y el ángulo de desfase, con la fórmula inversa del coseno:

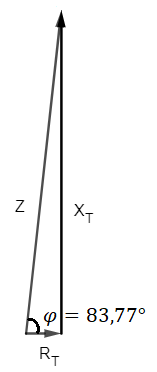
Nos queda el siguiente triángulo de impedancias:

El valor de la impedancia obtenido nos permite calcular también la intensidad del circuito, aplicando la ley de ohm, ya que conocemos la tensión:

Sustituimos valores y operamos:

Conocido el valor de la intensidad, de la resistencia total, de la reactancia total y de la impedancia, podemos calcular las potencias del circuito.

Calculamos la potencia activa:

Calculamos la potencia reactiva:

Y calculamos la potencia aparente:

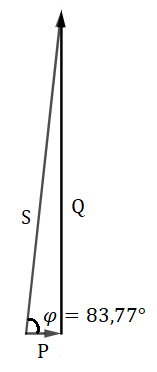
El triángulo de potencias nos queda de la siguiente forma:

Nos piden calcular la capacidad del condensador a instalar en paralelo para corregir el factor de potencia del conjunto a 0,95:

Con este coseno de φ, el nuevo ángulo de desfase será:

Es decir, al instalar un condensador en paralelo, a la potencia reactiva total inicial, que es inductiva, se le resta la potencia reactiva de la batería de condensadores, ya que al ser una potencia reactiva capacitiva, va en sentido contrario a la inductiva, obteniendo una nueva potencia reactiva Q’ más reducida, que si lo representamos en el triángulo de potencias tenemos:

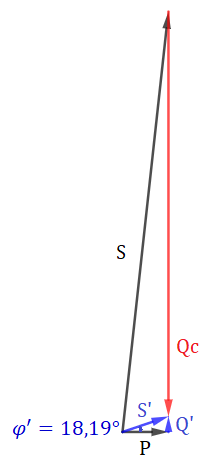
Nos queda por tanto un nuevo triángulo de potencias, donde ahora la potencia reactiva total es Q’ y por tanto, se ven modificadas la potencia aparente, que pasa a ser S’, el ángulo de desfase, que pasa a ser φ’ y por tanto, también se modifica el factor de potencia, que es lo que queremos conseguir.

Para calcular la potencia reactiva del condensador utilizamos la siguiente fórmula:

Sustituimos valores y operamos:

Esta es al potencia reactiva que restaríamos a la potencia reactiva inicial si quisiéramos obtener el valor de la potencia reactiva final Q’, una vez corregido el factor de potencia.

Con el valor de la potencia reactiva, podemos calcular la intensidad que circula por el condensador:

Y una vez conocida la intensidad que circula por el condensador, calculamos la reactancia capacitiva, aplicando la ley de ohm:

Sabemos que la reactancia capacitiva también se calcula con la siguiente fórmula:

De donde despejamos la capacidad del condensador:

Por último, sustituimos valores y operamos:

Por tanto, habría que instalar en paralelo un condensador de 6,89 μF de capacidad a 230 V y 115 VAr para que el factor de potencia del circuito sea igual a 0,95.

Ejercicio resuelto en circuitos trifásicos

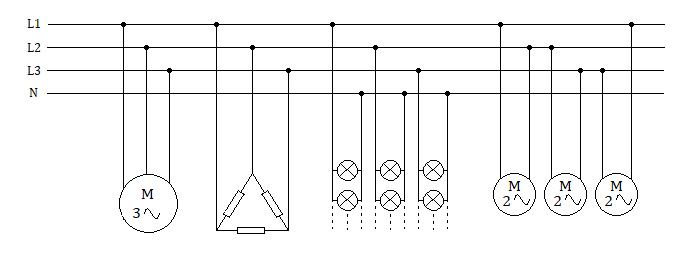
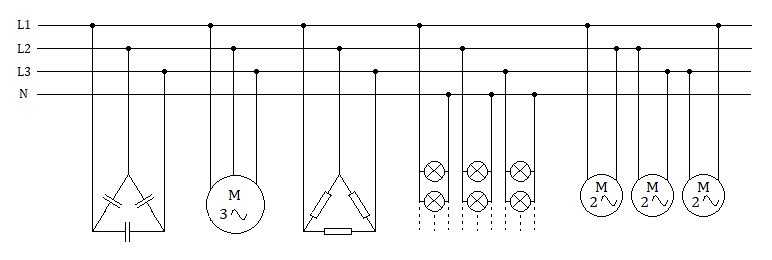
Una instalación eléctrica consta de los siguientes receptores conectados a una línea trifásica de 400 V:

• 1 motor trifásico de 10 kW y cos φ=0,75
• 1 horno trifásico  formado por tres resistencias de 50 Ω conectadas en triángulo
• 30 lámparas de vapor de mercurio de 500 W, 230 V y cos φ=0,6, conectadas equitativamente entre fase y neutro
• 3 motores monofásicos de 2 kW, 400 V y cos φ=0,7 conectados entre fases

Calcular:

a) La potencia aparente total de la instalación

b) Intensidad consumida por la instalación

c) El factor de potencia de la instalación

Se instala en la cabeza de la instalación una batería de condensadores en triángulo para corregir el factor de potencia hasta 0,95.

Calcular:

d) Características de la batería de condensadores

Los apartados a, b y c de este ejercicio los tienes resuelto con todo detalle en la lección de Cálculo de instalaciones trifásicas con varios receptores. Aquí, dejaremos un pequeño resumen para tener los resultados de los tres primeros apartados y nos centraremos en resolver paso a paso el apartado d.

En primer lugar, calculamos las potencias activa y reactiva de cada receptor y una vez las tengamos, la potencia activa total será la suma de las potencias activas de cada receptor:

La potencia reactiva total será la suma de las potencias reactivas de cada receptor:

La potencia aparente total la calculamos con la fórmula:

Sustituimos los valores de la potencia activa total y la potencia reactiva total y operamos:

Una vez que conocemos la potencia aparente total de la instalación, ya podemos obtener la intensidad total que consume la línea, a partir de la fórmula para calcular la potencia aparente:

Despejamos la intensidad de línea, sustituimos valores y operamos:

Por último, calculamos el factor de potencia de la instalación, a partir del triángulo de potencias total de la instalación:

Ahora vamos a calcular las características de la batería de condensadores a instalar para corregir el factor de potencia de la instalación a 0,95.

Con la fórmula inversa del coseno, calculamos el ángulo de desfase inicial de la instalación:

Se desea que el nuevo factor de potencia sea igual a 0,95:

El nuevo ángulo de desfase será igual a:

Calculamos la potencia reactiva del condensador con la siguiente fórmula

Sustituimos valores y operamos:

La batería de condensadores a instalar debe tener una potencia reactiva de 21590,67 VAr.

Calculamos ahora la capacidad de cada uno de los condensadores que forma la batería de condensadores, por lo que obtenemos la potencia reactiva por fase dividiendo la potencia reactiva total entre 3:

En una conexión en triángulo, la tensión de línea es igual a la tensión de fase:

La tensión en caca fase de la batería de condensadores es:

Por otro lado, la potencia reactiva por fase es igual a la tensión de fase por la intensidad de fase:

De la fórmula anterior despejamos la intensidad que circula por cada fase de la batería de condensadores:

Sustituimos valores y operamos:

Además, en cada fase, la reactancia capacitiva es igual a la tensión de fase entre la intensidad de fase:

Sustituyendo valores y operando nos queda:

Finalmente, calculamos la capacidad del condensador de cada fase con la fórmula:

Sustituimos valores y operamos:

La batería de condensadores a instalar deberá tener una potencia de 21590,67 VAr a 400 V y está formada por 3 condensadores de 143 μF a 400 V conectados en triángulo.

¿Necesitas ayuda en electrotecnia y matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar.

He diseñado un método práctico y efectivo que te ayudará a entender la electrotecnia así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas de electrotecnia
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?

Te explicaré lo que necesitas aprender para entender electrotecnia y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender electrotecnia y matemáticas? Pulsa el botón para saber más:

ENSÉÑAME ELECTROTECNIA