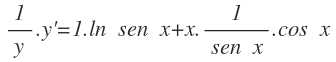A continuación te voy a explicar en qué consiste el método de la derivación logarítmica y en qué casos hay que aplicarlo, con ejercicios resueltos paso por paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cuando usar el método de la derivación logarítmica
Existen fórmulas de funciones derivadas calcular la derivada de una función potencial, es decir, cuando la x o una función están elevadas a un número:
De la misma forma, existen fórmulas de funciones derivadas calcular la derivada de una función exponencial, es decir, cuando un número está elevado a x o a una función:
Sin embargo, no tenemos ninguna fórmula para derivar funciones que sean potenciales y exponenciales a la vez, es decir que tanto las x o las funciones estén en la base y en el exponente:
Por tanto, con este tipo de funciones potenciales-exponenciales es cuando hay que utilizar el método de la derivación logarítmica.
En el siguiente apartado veremos cuál es su procedimiento. Para entenderlo bien, es necesario que tengas muy claro cómo derivar funciones logarítmicas y como aplicar la regla de la derivada de un producto. Si necesitas revisarlo, en el Curso de Derivadas lo tienes explicado paso a paso, en el que te enseño a derivar paso a paso desde el principio.
Procedimiento del método de la derivación logarítmica
El procedimiento para derivar funciones potenciales-exponenciales mediante el método de la derivación logarítmica es el siguiente:
- Aplicar logaritmos neperianos a ambos miembros de la ecuación
- Aplicar propiedades de los logaritmos pasando la función exponente a multiplicar al logaritmo del segundo miembro
- Derivar por separado ambos miembros de la ecuación, teniendo en cuenta que la «y» del primer miembro es una función compuesta y por tanto hay que multiplicar por su derivada y’
- Despejar y’
- Operar en el segundo miembro para simplificar
- Sustituir el valor de «y» por su valor, el cual lo obtenemos de la ecuación original
Resolviendo unos cuantos ejercicios lo entenderás mejor, que es lo que haremos en el siguiente apartado.
Ejercicios resueltos del método de la derivación logarítmica
Vamos a resolver un par de ejercicios para que te quede más claro cuáles son los pasos de la derivación logarítmica.
Por ejemplo:
Aplicamos logaritmos neperianos en ambos miembros de la ecuación:
Aplicamos las propiedades de los logaritmos, pasando a multiplicar al logaritmo la función que hacía de exponente, en el segundo miembro:
Derivamos en ambos miembros de la igualdad. En el primer miembro, derivamos con respecto de «y», considerando «y» como una función compuesta y por lo tanto, hay que multiplicar por su derivada que es y’.
En el segundo miembro, aplicamos la regla de la derivada de un producto:
Operamos en el segundo término del segundo miembro, ya que se anulan las x:
Ahora debemos despejar y’ (la derivada de y). Para ello, primero pasamos multiplicando la «y» a todo el segundo miembro:
Por último, debemos sustituir la «y» por su valor y eso lo obtenemos de la ecuación original:
Por tanto, sustituyendo la «y» nos queda:
Y ese sería el valor de la derivada.
Vamos a ver otro ejemplo:
Empezamos aplicando logaritmos neperianos en ambos miembros de la ecuación:
Aplicamos propiedades de los logaritmos pasando a multiplicar la x del exponente al logaritmo neperiano:
Derivamos por separado ambos miembros de la ecuación:
Ahora vamos a operar en el segundo miembro teniendo en cuenta que el coseno entre el seno es igual a la cotangente:
Realizando este cambio nos queda de la siguiente forma:
Despejamos la y’ pasando la «y» al segundo miembro multiplicando:
Sustituimos la «y» por su valor, obtenido de la ecuación original, llegando a la obtención de su derivada:
Como ves, el procedimiento para derivar funciones potenciales-exponenciales por el método de la derivación logarítmica es siempre igual, por lo que si has entendido cómo he resuelto estos dos ejercicios, sabrás resolverlos todos.
Si necesitas aprender a derivar, te recomiendo el Curso de Derivadas, en el que empezamos a derivar funciones muy sencillas y terminados derivando todo tipo de funciones, con ejercicios resueltos paso a paso y propuestos con la solución para practicar.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: