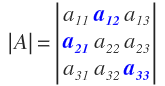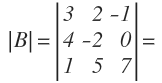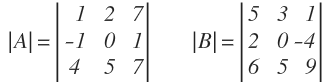Vamos a ver qué son los determinantes y te explicaré cómo calcular determinantes de orden 2 y de orden 3, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué son los determinantes
Un determinantes es un número asociado a una matriz cuadrada.
Este número permite estudiar y analizar un sistema de ecuaciones lineales, analizar si una matriz tiene matiz inversa y calcular esa matriz inversa.
Vamos a ver ahora cómo se calcula el determinante de una matriz cudrada.
Cómo se calcula un determinante de orden 2
El determinante de una matriz cuadrada de orden dos se calcula como producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria.
En general, para una matriz cuadrada de orden 2:
Los elementos de la diagonal principal son los elementos situados en la diagonal que va desde la esquina superior izquierda hasta la esquina inferior derecha:
Los elementos de la diagonal secundaria son los elementos situados en la diagonal que va desde la esquina superior derecha hasta la esquina inferior izquierda:
Por tanto, el determinante de una matriz cuadrada de orden 2 se calcular de la siguiente forma:
Ejercicio resuelto de determinante de orden dos
Vamos a ver un ejemplo de cómo se resuelve un determinante de orden 2.
Calcular el determinante asociado a la siguiente matriz cuadrada:
El determinante de esa matriz cuadrada es:
Para calcularlo, realizamos el producto de los elemento de la diagonal principal menos el producto de los elementos de la diagonal secundaria:
Y operamos:
El determinante de la matriz A es igual a 2.
Cómo se calcula un determinante de orden 3
Vamos a explicar cómo se calcula el determinante asociado a una matriz cuadrada de orden 3, también llamado como un determinante de orden 3.
Para una matriz de orden 3:
Su determinante de orden 3 será:
Para calcular este determinante, podemos utilizar la regla de Sarrus. Esta regla sólo funciona para los determinantes de orden 3. Para determinantes de orden 4 o superior, se utiliza otro procedimiento, que lo tienes explicado en otra lección.
Regla de Sarrus
Para que te queda muy claro, vamos a ir viendo paso a paso cómo aplicar la regla de Sarrus, al mismo tiempo que vamos resolviendo un determinante de orden 3.
Vamos a calcular el siguiente determinante de orden 3 por la regla de Sarrus:
Un determinante de orden 3 es igual a:
- El producto de los elementos de la diagonal principal
Este producto nos queda de la siguiente manera:
- Más el producto de los elementos de la línea paralela superior a la diagonal principal por el elemento del vértice opuesto a esa línea
Que se lo añadimos al desarrollo:
- Más el producto de los elementos de la línea paralela inferior a la diagonal principal por el elemento del vértice opuesto a esa línea
Que nos queda:
- Menos el producto de los elementos de la diagonal secundaria:
- Menos el producto de los elementos de la línea paralela superior a la diagonal secundaria por el elemento del vértice opuesto a esa línea
- Menos el producto de los elementos de la línea paralela inferior a la diagonal secundaria por el elemento del vértice opuesto a esa línea
Por tanto, el determinante de una matriz cuadrada de orden 3:
Es igual:
Nos queda operación compuesta por 6 términos. Los términos que están en el sentido de la diagonal principal están sumando y los términos que quedan en el sentido de la diagonal secundaria están restando. Además cada término está compuesto por 3 elementos.
Para que se sea más fácil de recordar al regla de Sarrus, ten en cuenta que siempre debes ir multiplicando 3 elementos. Por tanto, cuando te falte un elemento lo tienes en el vértice opuesto del determinante.
Ejercicios resueltos de determinantes de orden 3
Vamos a resolver unos ejercicios sobre calcular determinantes de orden 3.
Ejercicio 1
Calcula el determinante de orden 3 asociado a la siguiente matriz cuadrada:
El determinante de esa matriz cuadrada es:
Aplicamos la regla de Sarrus y queda:
Y operamos:
El determinante de la matriz A es igual a 0.
Ejercicio 2
Calcular el siguiente determinante de orden 3:
En este caso, tenemos elementos que son números negativos. Por tanto, hay que tener en cuenta por un lado la regla de los signos a la hora de multiplicar los elementos entre sí y por otro, el signo que precede a cada término según le corresponda por la aplicación de la regla de Sarrus.
Por tanto, en primer lugar aplicamos la regla de Sarrus:
Y después operamos teniendo en cuenta la regla de los signos:
Ejercicios propuestos
1- Calcula los siguientes determinantes de orden 2:
2- Calcula los siguientes determinantes de orden 3:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

Exámenes resueltos de Matemáticas II Selectividad (EvAU) Castilla-La Mancha

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Asturias

Exámenes resueltos de Matemáticas II Selectividad (PevAU) Andalucía

Exámenes resueltos de Matemáticas II Selectividad (EBAU) La Rioja

Exámenes resueltos de Matemáticas II Selectividad (EBAU) Castilla y León

Exámenes resueltos de Matemáticas II Selectividad (EvAU) Navarra

Exámenes resueltos de Matemáticas II Selectividad (PAU) Valencia