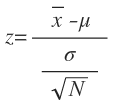A continuación vamos a ver qué es la media muestral y cómo se distribuyen las medias de una distribución muestral, con ejercicios resueltos paso a paso.
¡Vamos allá!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
La media muestral
La inferencia estadística trata de averiguar características de una población, a partir del estudio de una muestra.
Es decir, para conocer tendencias o datos de una población, como por ejemplo puede ser un país, como no es posible encuestar a todo el país, lo que se hace es encuestar un conjunto de individuos que pertenezca a esa población o lo que es lo mismo, una muestra de la población.
Por ejemplo, queremos conocer cual es la estatura media en un determinado país.
¿Qué tendría que hacer para obtener esta estatura media?
Pues para hacerlo exacto, tendría que medir a todos los habitantes del país y obtener la media.
Como no es posible hacer esto, lo que se hace es obtener una muestra de los habitantes del país y de este conjunto de individuos calculo su media. La media de la muestra es lo que se llama la media muestral y se representa de la siguiente manera:
La muestra debe ser representativa fiel que refleja la población. Para ello, esta muestra debe mantener las mismas proporciones que la población total (hombres y mujeres, edades…).
Existen diferentes tipos de muestreos, pero en esta lección no nos detendremos en eso sino que nos centraremos en aprender a resolver ejercicios.
Distribución de la media muestral
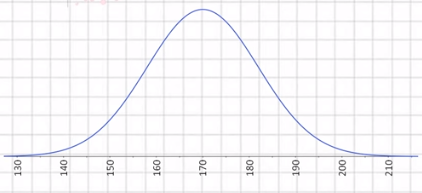
Supongamos que sabemos que la altura de un determinado país sigue una distribución normal de media 170 y desviación típica 12 N(170,12):
Cuya curva de distribución normal sería como ésta:
Ahora imaginemos que tomamos una muestra de tamaño N, donde N es el número de personas y a estas personas les calculo su media muestral.
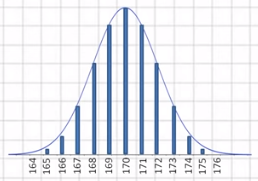
Si tomo diferentes muestras y voy calculando su media muestral, voy obteniendo diferentes valores de la media muestral, que si las represento en una tabla de frecuencias, vemos que a su vez, los valores de las medias muestrales forman otra curva de distribución normal:
Si nos detenemos a analizar estas dos curvas de distribución normal (la de la población y la de las muestras) vemos que ambas tienen la misma media (170).
También vemos que la forma en la que se distribuyen las medias de una muestra es una curva normal mucho más compacta, donde los valores están más cerca del valor central, por lo que la desviación típica de la curva normal de las muestras será menor y se calcula mediante la siguiente fórmula:
Donde N es el número de individuos de la muestra.
De esta fórmula se deduce, que cuantos más individuos haya en la muestra, la desviación típica será más pequeña, lo que quiere decir que las medias, se concentrarán todavía más en torno al valor central y se acercarán más a la media de la población.
Por tanto, si la población sigue una distribución normal de media μ y desviación típica σ:
La distribución normal de las medias muestrales, tendrá la misma media que la población, pero la desviación típica estará dividida entre raíz de N:
Ejercicios resueltos de distribución de la media muestral
Ejercicio 1
La duración media de las bombillas de una determinada marca sigue una distribución normal N(1500,160)
a) Si escogemos una bombilla al azar, ¿cuál es la probabilidad de que funcione más de 1524 horas?
b) Si escogemos una muestra de 100 bombillas y calculamos su duración media, ¿cuál es la probabilidad de que sea superior a 1524 horas?
Apartado a:
Si escogemos sólo una bombilla, estamos teniendo en cuenta toda la población que sigue una distribución normal de media μ y desviación típica σ N(μ,σ):
Que en nuestro caso es:
Nos preguntan la probabilidad de que una bombilla funcione más de 1524 horas, es decir:
Por tanto, lo primero que tenemos que hacer es tipificar la x:
Sustituyo valores y obtengo el valor de z:
La probabilidad de durar más de 1524 horas es igual a la probabilidad de que z sea mayor que 0,15 y para poder utilizar la tabla de distribución normal, eso es igual a 1 menos la probabilidad de que z sea menor o igual a 0,15:
La probabilidad de que z sea menor o igual a 0,15 la obtengo directamente de la tabla y me da:
Sustituyo este valor y calculo:
Por tanto, la probabilidad de que una bombilla funcione más de 1524 horas es de 44,04% o lo que es lo mismo el 44,04% podría durar más de 1524 horas.
Apartado b:
Si tomamos un muestra de 100 bombillas la distribución normal tiene la misma media que la población, pero la desviación típica estará dividida entre raíz de N:
Me piden cuál es la probabilidad a que la duración media de esa muestra sea superior a 1524 horas:
Tipificamos la media, pero teniendo en cuenta la nueva desviación típica:
Sustituyo datos y calculo:
La probabilidad de la media sea superior 1524 horas es igual a la probabilidad de que z sea mayor que 1,5 y para poder utilizar la tabla de distribución normal, eso es igual a 1 menos la probabilidad de que z sea menor o igual a 1,5:
Obtengo la probabilidad de que z sea menor o igual a 0,15 directamente de la tabla:
Sustituyo este valor y calculo:
Hay un 6,68% de probabilidad de que si tomo una muestra de 100 bombillas, la media de su duración sea superior a 1524 horas.
Ejercicio 2
Los pesos de las ovejas de una cierta ganadería tienen una media de 50 kg con una desviación típica de 4. Elegimos al azar una muestra aleatoria simple de 100 ovejas. Determina:
a) La probabilidad de que su media sea superior a 51 kg.
b) La probabilidad de que su media sea inferior a 56 kg.
c) La probabilidad de que su media sea superior a 49 kg.
d) La probabilidad de que su media esté entre 49,5 kg y 50,3 kg.
La distribución normal de la población es:
Calculamos la desviación típica de la muestra, obteniendo la siguiente distribución normal para la muestra:
Con esta distribución contestaremos a los apartados del ejercicio.
Apartado a:
Nos preguntan la probabilidad de que la media de la muestra sea superior a 51 kg.
Tipificamos la media muestral, teniendo en cuenta la desviación típica de la distribución normal de la muestra:
La probabilidad de que la media sea mayor que 51 es igual a la probabilidad de que z sea mayor que 2,5 y para poder utilizar la tabla de distribución normal, eso es igual a 1 menos la probabilidad de que z sea menor o igual a 2,5:
Obtengo la probabilidad de que z sea menor o igual a 2,5 directamente de la tabla:
Y lo sustituyo en la operación anterior:
La probabilidad de que la media de la muestra sea superior a 51 kg es de un 0,62%. Es un porcentaje muy pequeño, ya que estamos muy cerca de 3,5 veces la desviación típica, a la derecha de la media y por encima de ese valor tendría un 0%.
Apartado b:
Nos preguntan la probabilidad de que la media de la muestra sea inferior a 56 kg.
Tipificamos la media muestral:
La probabilidad de que la media sea menor que 56 es igual a la probabilidad de que z sea menor que 15:
Si te das cuenta, la tabla de distribución estándar llega hasta z=3,99, lo que quiere decir que la probabilidad de que z sea menor que 4 es igual a 1 y pasa lo mismo con valores de las desviación típica mayores que 4, luego la probabilidad de que z sea menor que 15 también es igual a 1
La probabilidad de que la media de la muestra sea inferior a 56 kg es de un 100%
Apartado c:
Nos preguntan la probabilidad de que la media de la muestra sea superior a 49 kg.
Tipificamos la media muestral:
La probabilidad de que la media sea mayor que 49 es igual a la probabilidad de que z sea mayor que -2,5 y para poder utilizar la tabla de distribución normal, eso es igual a la probabilidad de que z sea menor o igual a 2,5, que lo obtenemos directamente de la tabla:
La probabilidad de que la media de la muestra sea superior a 49 kg es de un 99,38%
Apartado d:
Nos preguntan la probabilidad de que la media de la muestra esté entre 49,5 kg y 50,3 kg.
Tipificamos las medias muestrales:
La probabilidad de que la media esté entre 49,5 y 50,3 es igual a la probabilidad de que z esté entre -1,25 y 0,75:
Que es igual a la siguiente expresión tal y como explico en lección de cómo utilizar la distribución normal N(0,1):
Directamente de la tabla obtenemos la probabilidad de que z sea menor o igual a 0,75 y la probabilidad de que z sea menor o igual a 1,25
Sustituimos los valores en la operación anterior y operamos:
La probabilidad de que la media de la muestra esté entre 49,5 kg y 50,3 kg es de un 66,78%
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: