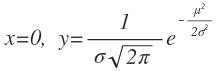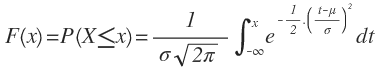A continuación te voy a explicar qué es la distribución normal y veremos cuáles son sus propiedades para entender cómo funciona.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es la distribución normal
La distribución normal es un modelo de distribución muy utilizado para variables continuas, que se ajusta a un gran número de variables de nuestro entorno. También es conocida como distribución de Gauss.
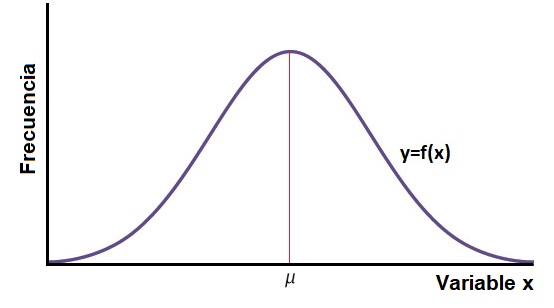
Si representamos los datos de una determinada muestra en una tabla de frecuencias, donde en el eje x representamos la variable en cuestión y en el eje «y» su frecuencia, vemos que la curva de distribución normal tiene forma de campana:
Esta curva tiene una serie de características, que vamos a ver a continuación.
La gráfica recibe el nombre de curva o campana de Gauss, ya que tiene forma de campana.
Los parámetros de una distribución normal son la media μ y la desviación típica σ y se designa por N(μ,σ).
Como ves en la gráfica, la media μ está justo en el centro y es el valor que más se repite, por lo que también es la moda.
La curva es simétrica con respecto a la media, es decir, tiene la misma forma a la derecha que a la izquierda de la media.
La desviación típica σ nos marca la homogeneidad de los valores, es decir, lo cerca o lejos que están todos los valores de la media. Si los valores están muy concentrados con respecto a la media, la desviación típica tendrá un valor muy bajo y la curva tendrá una forma más afilada. Si los valores estás más repartidos y se alejan mucho de la media, la desviación típica tendrá un valor muy alto y la curva tendrá una forma más achatada.
Por ejemplo, en esta imagen tenemos varias curvas de distribución normal con distinta desviación típica. Observa como cuanto mayor es la desviación típica, la curva es más achatada:
Entre las variables que se distribuyen con una distribución normal podemos encontrar las que se refieren a aspectos físicos, psicológicos, sociológicos, como pesos, diámetros, alturas, cociente intelectual, puntuación de un examen, etc.
Por ejemplo, las estaturas de una determinada población siguen una distribución normal. Si medimos las estaturas de la población y la representamos en una tabla de frecuencias, donde en el eje x se representa la estatura y en el eje «y» la cantidad de personas, nos queda algo así:
Podemos observar que la mayoría de la población se concentra en el centro, es decir, mide entre 160 y 180 cm y el valor que más se repite es 170, que es la media. Muy pocas personas miden 190 y muy pocas personas miden 145. La gráfica tiene forma de campana.
Existen muchas variables continuas en las que la representación gráfica de una muestra tiene forma de campana, siguiendo este modelo de distribución normal.
Función de densidad de la distribución normal
La curva de la distribución normal viene determinada por una función llamada función de densidad, cuya fórmula es la siguiente:
Por tanto, según Gauss, si conocemos los valores de la media μ y la desviación típica σ y representamos la función, obtenemos la curva de una distribución normal en forma de campana.
Por supuesto que esta fórmula no es necesario aprendérsela. Solamente la indicamos para saber de dónde sale la curva de la distribución normal y cómo se comporta para poder trabajar con ella posteriormente.
Propiedades de la función densidad de la distribución normal
Conocer las propiedades de la función densidad f(x) de una distribución normal N(μ,σ), cuya gráfica sabemos que tiene forma de campana, hará que comprendamos mejor dicha distribución así como su aplicación.
Las principales propiedades son las siguientes:
Dominio
El dominio es todo R, es decir, (-∞,∞). Para valores superiores a 4 o inferiores a -4, los valores que toma la función son poco significativos.
Simetrías
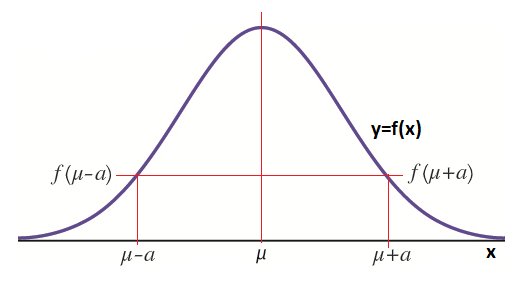
La función es simétrica con respecto de la recta vertical x=μ, ya que se cumple que para cualquier número real «a», f(μ+a)=f(μ-a):
Cortes con los ejes
La curva de la distribución normal no corta al eje de abcisas o el eje x. Corta al eje de ordenadas o eje «y» en el siguiente punto:
Extremos
La función no tiene mínimos. Tiene un máximo en el punto x=μ
Monotonía
La función es creciente hasta la recta vertical x=μ y a partir de ese punto es decreciente.
Puntos de inflexión
La curva tiene dos puntos de inflexión en los valores de abcisas: x=μ-σ y x=μ+σ:
Área encerrada bajo la curva
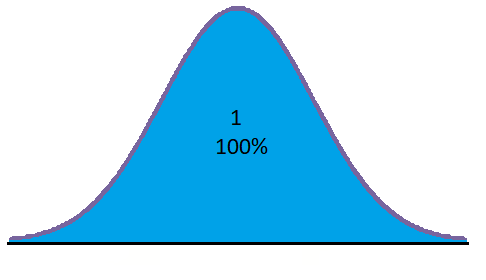
El área comprendida entre la curva y el eje x es igual a 1. Si calculamos el área mediante la integral entre menos infinito e infinito de la función, su resultado es igual a 1:
Es decir, representa la probabilidad del suceso seguro. Si la expresamos en porcentaje, este valor sería del 100%.
Si elegimos dos valores a y b, el área encerrada entre la curva, el eje x y las ordenadas en los puntos a y b es la probabilidad de obtener un valor x entre a y b:
El área encerrada entre la curva, el eje x y dos valores cualesquiera, las podemos traducir en porcentaje de la muestra o en probabilidad.
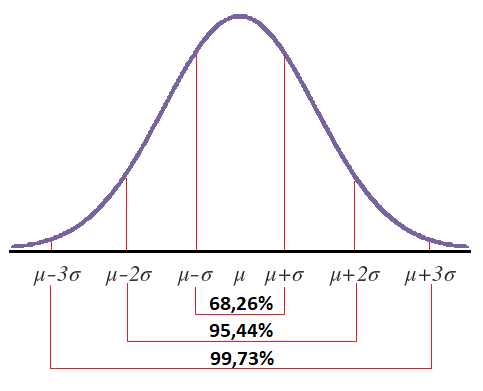
Áreas en ciertos intervalos
En la distribución normal N(μ,σ) se cumple que:
- En el intervalo (μ-σ, μ+σ) se encuentra el 68,26% del área total
- En el intervalo (μ-2σ, μ+2σ) se encuentra el 95,44% del área total
- En el intervalo (μ-3σ, μ+3σ) se encuentra el 99,73% del área total
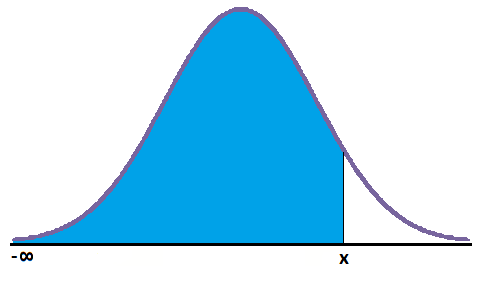
Función de distribución
Para una variable continua X que se ajusta a una distribución normal N(μ,σ), la función de distribución viene dada por la siguiente expresión:
donde F(x) representa el área encerrada bajo la curva de la función desde -∞ hasta x, es decir, el tanto por ciento de valores que están distribuidos entre -∞ y x:
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: