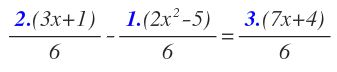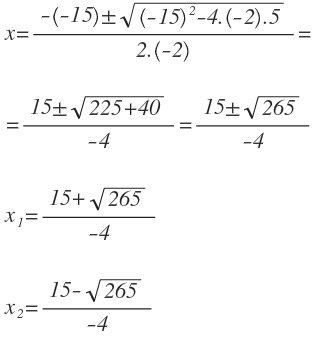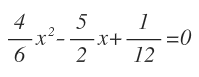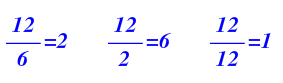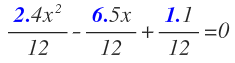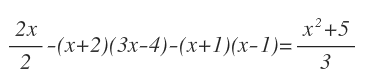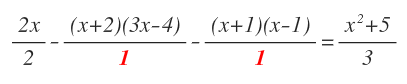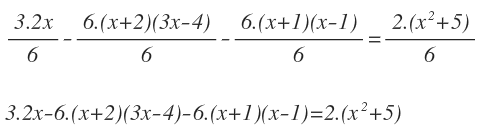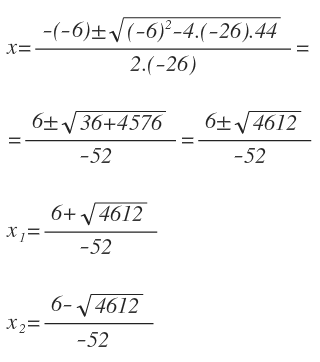A continuación te voy a explicar cómo resolver ecuaciones de segundo grado con denominadores y paréntesis, con ejercicios resueltos paso a paso.
En el curso de ecuaciones de segundo grado, tienes una lección donde explico más despacio y desde el principio cómo eliminar los paréntesis en una ecuación se segundo grado. Consúltala si lo necesitas.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo eliminar denominadores en ecuaciones de segundo grado
Eliminar los denominadores es el primer paso que debe realizarse para simplificar una ecuación de segundo grado.
Para ello, previamente hay que obtener el denominador común de todos los denominadores de la ecuación y después obtener cada fracción equivalente.
Vamos a verlo más despacio paso a paso. Por ejemplo, tenemos la siguiente ecuación:
Empezamos calculando el denominador común, que es el mínimo común múltiplo de los denominadores:
Las fracciones de la ecuación pasarán todas a tener como denominador 6 y las dejamos preparadas para calcular su nuevo denominador.
Para que las fracciones sean equivalentes, se debe multiplicar en el numerador y en el denominador por el mismo número.
Al colocar el denominador común, indirectamente ya hemos multiplicado el denominador original por un número. Por tanto, queda multiplicar el numerador por ese mismo número para que la fracción sea equivalente.
¿Pero cómo obtenemos ese número?
Se obtiene dividiendo el común denominador entre el denominador de la fracción original:
Por tanto, los números por los que hay que multiplicar cada numerador serían éstos:
Los colocamos multiplicando en su numerador correspondiente:
Hasta aquí hemos obtenido fracciones equivalentes a las originales, todas con el mismo denominador y cada una multiplicada por el mismo número en el numerador y en el denominador
Ahora ya podemos eliminar los denominadores. Eliminarlos es equivalente a multiplicar cada miembro por el denominador común, es decir, por 6 y nos queda:
El siguiente paso es eliminar los paréntesis. Éste paso es mejor hacerlo después de eliminar los denominadores para no cometer errores con los signos.
Date cuenta que aunque sea multiplicar por 1, lo hemos puesto. De esta forma no perdemos el signo menos que lleva delante la fracción. Muchas veces, se comete el error de no cambiar de signo a todos los términos que encierra el paréntesis.
Después de eliminar paréntesis nos queda:
Llevamos todos los términos al primer miembro:
Y agrupamos términos:
Quedándonos una ecuación de segundo grado completa que se resolvería que pasamos a resolver:
Recuerda que cuando un término no tiene denominador es lo mismo que si tienen un 1 y que no se pueden agrupar todos los términos que no tienen denominador en una sola fracción con denominador 1.
Por ejemplo, en esta ecuación:
Cada término sin denominador tendría un 1:
Pero no es correcto hacerlo así:
Ya que por ejemplo el signo menos que sólo afecta a 3x, al agrupar en una misma fracción también hacemos que afecte al 6, por lo que estaríamos modificando la ecuación.
Ecuaciones de segundo grado con fracciones
Una variante de las ecuaciones de segundo grado con denominadores es cuando aparecen fracciones.
Se diferencian de las anteriores en que cuando aparecen fracciones, los denominadores sólo afectan a un término. No tenemos fracciones cuyos numeradores tienen sumas o restas en el numerador, es decir, en el numerador sólo hay un término.
El procedimiento para eliminar los denominadores en el caso de las fracciones es el mismo que el que he explicado en el apartado anterior.
Vamos a verlo con un ejemplo:
Vemos en esta ecuación como x² y x están multiplicadas por una fracción, aunque no lo parezca. Antes de obtener factor común, debemos realizar esas multiplicaciones
Las fracciones se multiplican en línea. Para multiplicar cada fracción por x² y x se multiplican por el numerador y los denominadores se multiplican por 1, quedando de la siguiente manera:
Ahora ya podemos obtener común denominador, que es el mínimo común múltiplo de los denominadores:
Calculamos el número por el que debemos multiplicar el numerador de cada fracción:
Y multiplicamos numeradores:
Eliminamos el denominador:
Y finalmente operamos:
Nos queda una ecuación de segundo grado completa que habría que resolver con la fórmula general.
Quitar denominadores en las ecuaciones es tener claro cómo calcular sus fracciones equivalentes a partir del denominador común.
Hay que estar muy atentos con los signos, sobre todo con los signos menos que están delante de las fracciones, ya que cuando eliminemos los denominadores, cambiarán de signo a todos los términos del numerador.
Para evitar esto, es mejor multiplicar paréntesis después de eliminar denominadores.
Y ahora te dejo con unos ejercicios para que practiques y compruebes si lo has entendido todo.
Ejercicio resueltos de ecuaciones de segundo grado con denominadores
Resuelve las siguientes ecuaciones de segundo grado:
Con lo explicado hasta ahora, has aprendido a resolver las ecuaciones de segundo grado con denominadores.
Tan solo nos queda un paso más para que aprendas a resolver todas las ecuaciones de segundo grado y ese paso es que tengas denominadores y paréntesis en la misma ecuación.
Pues eso es justo lo que vamos a ver en el siguiente apartado. Empezaremos viendo los pasos a seguir y resolveremos un par de ejemplos.
Pasos para resolver ecuaciones de segundo grado sin simplificar
Es muy difícil encontrarnos ecuaciones de segundo grado simplificadas y preparadas para poder resolverlas. Lo más normal es que nos enfrentemos a ecuaciones con denominadores, paréntesis y potencias.
Los pasos a seguir para simplificar una ecuación de segundo grado que tenga denominadores y paréntesis son los siguientes:
- Eliminar paréntesis y corchetes que impidan eliminar denominadores
- Eliminar denominadores
- Eliminar paréntesis y corchetes
- Pasar todos los términos al primer miembro
- Agrupar términos semejantes
- Aplicar el método de resolución que corresponda, dependiendo si nos queda una ecuación de segundo grado completa o incompleta
Conforme vamos avanzando en los pasos, la ecuación se irá volviendo más sencilla.
Si no sabes qué paso es el siguiente en el momento de resolver tu ecuación, pregúntate si lo que vas a hacer puede hacerse o hay algo que te lo impide.
Si hay algo que te lo impide, entonces vuelve a preguntarte lo mismo para eliminar ese algo y si no hay nada, ese será el siguiente paso.
Por ejemplo: ¿puedo multiplicar este paréntesis por el número que tiene delante? No, porque el paréntesis está elevado al cuadrado, antes debo resolverlo.
¿Puedo resolver el cuadrado del paréntesis? Sí (has encontrado el primer paso)
Ejemplos de ecuaciones de segundo grado con denominadores y paréntesis
Como mejor se aprende es con ejemplos, así que empecemos. Tenemos la siguiente ecuación:
Empezamos eliminando los denominadores. ¿Hay algo que lo impida? No, pues adelante.
El denominador común es el 15 y después de calcular los números por los que hay que multiplicar los numeradores y por último multiplicamos cada numerador por su número correspondiente:
Eliminamos los denominadores:
Ahora vamos con los paréntesis. Empezamos aplicando la fórmula del cuadrado de una resta en el paréntesis que está al cuadrado. Además se pueden multiplicar números dentro de los términos
Fíjate como he encerrado entre paréntesis el resultado de desarrollar el cuadrado de una resta, ya que todo está multiplicado por -3.
Ahora opero dentro del paréntesis del primer miembro, multiplicando números y resolviendo cuadrados y en el segundo miembro ya multiplico el número por el paréntesis:
Ya sólo me queda un paréntesis que lo resuelvo multiplicando por -3 todos los términos que encierra
Hemos eliminado también los paréntesis. Ahora paso todos los términos al primer miembro:
Y agrupo términos semejantes:
Una vez simplificada, ha quedado una ecuación de segundo grado completa que resolvemos con la fórmula general:
Si te has dado cuenta en cada paso a veces puedo hacer más de una operación al mismo tiempo, pero sólo avanzo un paso en cada término. Es decir, no hago de memoria varias operaciones y después lo escribo.
Puedes hacerlo siempre que sepas lo que estás haciendo. Todo tiene que tener un por qué. Si lo haces sin entenderlo estarás abocado a tener un fallo.
Vamos con otro ejemplo:
En esta ecuación podríamos empezar multiplicando los paréntesis primero, ya que no hay ninguna operación previa que lo impida y obviamente, llegaríamos al mismo resultado.
Aun así vamos a empezar por eliminar denominadores, siguiendo el procedimiento que hemos empezado.
Los términos que no tienen denominador, tienen un 1 que normalmente no se escribe. Además ten en cuenta que los términos están separados por los signos más y menos, por lo que (x+2)(3x-4) y (x+1)(x-1) son dos términos:
Aclarado eso, obtenemos el común denominador:
Y calculamos los números por los que hay que multiplicar los numeradores:
Procedemos a multiplicar los numeradores y a eliminar denominadores:
Ahora nos centramos en eliminar los paréntesis.
Con (x+2)(3x-4) hay que multiplicar todos los términos de los paréntesis. El resultado lo encerramos entre paréntesis porque está multiplicado todo por -6.
(x+1)(x-1) se resuelve con una de las fórmulas de los productos notables, más concretamente con la de suma por diferencia. Volvemos a colocar el resultado entre paréntesis ya que también está multiplicado por -6.
Y en el segundo miembro podemos multiplicar el número por el paréntesis.
Como ves, en el mismo paso para la ecuación, realizamos un paso para cada término, pero sólo uno.
Te recomiendo, sobretodo al principio, no realizar varios pasos de cabeza y luego escribirlo, para ahorrarte pasos, ya que tienes muchas posibilidades de cometer un error.
En el siguiente paso, operamos dentro de los paréntesis:
Y ahora multiplicamos cada paréntesis por el número que tiene delante:
Una vez hemos eliminado también los paréntesis, pasamos todos los términos al primer miembro:
Y reagrupamos términos, quedándonos una ecuación de segundo grado completa:
Que pasamos a resolverla:
Ejercicios resueltos de ecuaciones de segundo grado con denominadores y paréntesis
Resuelve las siguientes ecuaciones:
Si lo has entendido todo, ahora no tienes ningún problema para resolver cualquier ecuación de segundo grado. Sólo necesitas un poco de práctica y si no, siempre tienes el curso de ecuaciones de segundo grado, donde tienes explicado todo desde el principio.
Déjame darte un último consejo:
Cuando las ecuaciones tienen paréntesis y denominadores hay que dar numerosos pasos. Evidentemente, con práctica podrás realizar varios pasos al mismo tiempo, pero al principio no te lo recomiendo por dos razones:
- Te permite detectar los errores en el caso de que los cometas cuando repases la ecuación
- A veces, el operar de memoria puede llevar a error. Escribir todos los pasos permite a tu mente descansar y no hacerla trabajar en exceso, sobre todo en los exámenes.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: