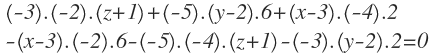Ecuaciones del plano. Ejercicios resueltos paso a paso.

A continuación te voy a explicar cómo expresar todas las formas de las ecuaciones de un plano. Al igual que una recta, el plano tiene la ecuación vectorial, las ecuaciones paramétricas y las ecuaciones implícitas. Con ejercicios resueltos paso a paso.

Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Un plano no tiene ecuación contínua.

Para definir una recta, necesitamos saber un punto por donde pasa y un vector de dirección. En este caso, un plano queda definido por al conocer un punto por donde pasa y dos vectores de dirección, ya que al tener un plano dos dimensiones, cada vector director indica una dimensión del plano.

Comentar también que un plano queda definido si conocemos tres puntos que pertenezcan al plano y estos no están alineados, ya que si estuvieran alineados, formarían una recta (veremos este caso con un ejercicio más abajo).

Empezamos explicando cada una de las ecuaciones del plano.

Ecuación vectorial del plano

Como comentábamos al principio, un plano queda definido por un punto por donde pase y dos vectores de dirección, que también son los datos que necesitamos para obtener la ecuación vectorial del plano.

Tenemos un punto P0 por donde pasa el plano:

Un vector de dirección:

Y otro vector de dirección:

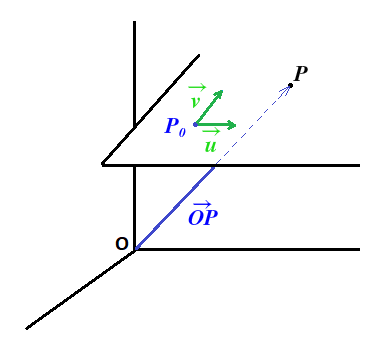
Tal y como se representa en la siguiente imagen:

Si tomamos un punto cualquiera del plano, como el punto P:

La ecuación vectorial del plano se determina por el vector OP, que es el vector que tiene origen en el origen de coordenadas y el extremo en ese punto P que pertenece al plano:

El vector OP se puede obtener como la suma vectorial de un vector con origen en el origen de coordenadas y extremo en el punto P0 (vector OP0), más otro vector con origen en el punto P0 y extremo en el punto P (vector P0P):

Que se representaría de la siguiente manera:

El vector PoP se puede expresar como una suma vectorial de los vectores de dirección multiplicados cada uno por un número, «t» y «s», tal que su longitudes sumen vectorialmente al vector PoP:

Que gráficamente sería:

Por tanto, la ecuación vectorial de un plano se expresa de la siguiente manera:

Y si ponemos cada vector en función de sus coordenadas, nos queda:

Que es la ecuación vectorial de un plano y se puede obtener directamente conocidos un punto perteneciente al plano y los dos vectores de dirección, donde X0, Y0 y Zo son las coordenadas del punto, U1, U2 y U3, las coordenadas de un vector de dirección, V1, V2 y V3, las coordenadas del otro vector de dirección:

Y «t» y «s» son dos números pertenecientes al conjunto de los números reales.

Ecuaciones paramétricas del plano

Las ecuaciones paramétricas de un plano se obtienen a partir de la ecuación vectorial:

Multiplicamos «t» y «s» por las coordenadas del vector de dirección al que multiplican:

Ahora sumamos los tres vectores, expresándolas en un sólo vector, coordenada a coordenada:

Finalmente, podemos escribir en expresiones separadas la ecuación de cada una de las coordenadas del vector que nos ha quedado en el segundo miembro, obteniendo las ecuaciones paramétricas del plano:

Donde Xo, Yo y Zo son las coordenadas del punto por donde pasa el plano, U1, U2 y U3 son las coordenadas de uno  de los vectores directores y V1, V2 y V3 son las coordenadas del otro vector director:

Las ecuaciones paramétricas del plano pueden obtenerse directamente si se conoce el punto por donde pasa el plano y ambos vectores de dirección, sustituyendo las coordenadas de cada uno por su valores correspondientes.

Ecuación implícita del plano

La ecuación implícita del plano se obtiene eliminando los parámetros «t» y «s», o lo que es lo mismo, resolviendo el sistema considerando «t» y «s» como incógnitas, y «x», «y» y «z» por tanto como términos independientes.

Así que, pasamos los términos independientes al segundo miembro:

La matriz de coeficientes sería en este caso:

Y la matriz ampliada:

Al ser la matriz de los coeficientes de dimensión 3×2, para calcular su rango, tendríamos que encontrar una submatriz cuadrada contenida en ella, cuyo determinante sea distinto de cero. Esta submatriz cuadrada sería de orden 2, por lo que el rango de A sería igual a 2:

Para que el sistema tenga solución, es decir, para que sea un sistema compatible determinado, el rango de la matriz ampliada también debe ser igual a 2:

Por tanto, para forzar a que el rango de la matriz ampliada sea igual a 2, su determinante debe de ser igual a cero:

De esta forma, desarrollamos el determinante de la matriz ampliada y lo igualamos a cero:

Llegando a la ecuación implícita del plano:

Siendo  el vector «n» de coordenadas (A,B,C) un vector normal (perpendicular) al plano, donde A, B y C son los coeficientes de la ecuación implícita del plano:

donde A, B, C y D son los coeficientes de la ecuación.

Coordenadas el vector normal (perpendicular) a un plano

Una vez tenemos la ecuación implícita del plano:

podemos obtener las coordenadas del vector «n», un vector normal (perpendicular) al plano, cuyas coordenadas son A, B y C:

siendo A, B y C los coeficientes de la ecuación implícita del plano.

Si realizamos el producto escalar del vector normal n, por el vector PoP (vector con origen en el punto P0 y extremo en el punto P y perteneciente al plano), su resultado es igual a cero, al formar un ángulo de 90º entre ambos vectores, con lo que también demostramos que ambos vectores son perpendiculares:

Cómo pasar de la ecuación implícita del plano a paramétricas y vectorial

Más arriba te he ido explicando cómo a partir de un punto y dos vectores de dirección se obtiene la ecuación vectorial y las ecuaciones paramétricas y cómo obtener la ecuación implícita a partir de las ecuaciones paramétricas.

Ahora te voy a enseñar el proceso contrario, es decir, partiendo de la ecuación implícita del plano, cómo obtener las ecuaciones paramétricas y por tanto, un punto y dos vectores de dirección del plano y hallar también la ecuación vectorial del plano.

Vamos a verlo resolviendo el siguiente ejercicio:

Escribe la ecuación vectorial y las ecuaciones paramétricas del siguiente plano expresado con su ecuación implícita:

En este ejercicio partimos de la ecuación implícita o general de un plano:

Tenemos que resolver este ecuación que depende de tres incógnitas. Para que tuviera solución, el número de ecuaciones debería ser igual al número de incógnitas, así que nos faltan dos ecuaciones.

En primer lugar, despejamos una de las incógnitas, dejándola en función de las otras dos. En este caso, despejaremos la «y», al ser la única que no está multiplicada por un coeficiente, evitando así tener denominadores. Nos queda:

Ahora vamos a añadir las dos ecuaciones que nos faltan.  A x le asignamos el parámetro t:

Y a z le asignamos el parámetro s:

En la ecuación en la que despejamos la «y», sustituimos x y z por sus nuevos valores:

Obteniendo el un sistema compatible indeterminado, de tres ecuaciones con tres incógnitas, que a su vez, se corresponde con las ecuaciones paramétricas del plano:

A partir de las ecuaciones paramétricas, obtenemos directamente un punto perteneciente al plano y dos vectores de dirección:

Y una vez tenemos el punto y los vectores de dirección, ya podemos obtener la ecuación vectorial:

Ejercicios resueltos sobre ecuaciones del plano

Vamos a resolver ahora unos ejercicios paso a paso para aplicar todo lo aprendido hasta ahora.

Ejercicio 1

Expresa las ecuaciones del plano en todas sus formas, determinado por el punto:

Y los vectores de dirección:

Empezamos con la ecuación vectorial:

Sustituimos  Xo, Yo y Zo por las coordenadas del punto y tanto U1, U2, U3 como V1, V2, V3, por las coordenadas de cada vector de dirección:

Seguimos con las ecuaciones paramétricas:

Igual que antes sustituimos las coordenadas del punto y las de los vectores de dirección por sus valores:

Por último vamos a obtener la ecuación implícita. Consideramos «t» y «s» como las incógnitas y «x», «y» y «z» pasan a ser términos independientes, por lo que los pasamos al segundo miembro:

La matriz de los coeficientes es:

Y la matriz ampliada es:

Vamos a calcular el rango de A, para ello, vamos a seleccionar la mayor submatriz cuadrada contenida en ella, cuyo determinante sea distinto de cero. Seleccionamos el que está formado por las filas 1 y 2 y las columnas 1 y 2:

Calculamos su determinante:

El determinante es distinto de cero, por lo que el rango es igual a 2, que coincide con el orden de la submatriz:

Para que el sistema tenga solución, el rango de la matriz ampliada también debe ser igual a 2:

El rango de la matriz ampliada será igual a 2, si su determinante es igual a cero:

Por tanto, forzamos a que su determinante sea igual a cero:

Desarrollamos el determinante con la regla de Sarrus, igualando su resultado a cero:

En el primer miembro, multiplicamos los números que nos quedan fuera de los paréntesis y anulamos los términos que están multiplicados por cero:

Eliminamos paréntesis:

Operamos y reordenamos términos, obteniendo por fin la ecuación implícita del plano:

Ejercicio 2

Hallar la ecuación implícita del plano que pasa por los puntos A, B y C:

Como te indiqué al principio de la lección, un plano queda determinado si conocemos 3 puntos que estén contenidos en el plano.

Para poder obtener las rectas conociendo 3 puntos, uno de ellos lo consideramos como P0, es decir, como un punto que pertenece al plano y con los otros dos formamos los vectores de dirección.

Vamos a verlo.

Vamos a dejar el punto A, como el punto que pertenece al plano:

El primer vector de dirección lo calcularemos como un vector con origen en el punto A y extremo en el punto B:

El segundo vector de dirección, tiene origen en el punto A y extremo en el punto C:

Una vez tenemos el punto y los dos vectores de dirección, obtenemos las ecuaciones paramétricas, ya que las necesitamos para después calcular la ecuación implícita.

Las ecuaciones paramétricas las obtenemos sustituyendo los valores de las coordenadas del punto y de los vectores de dirección, que nos queda:

Ahora consideramos «t» y «s» como las incógnitas y «x», «y» y «z» como términos independientes, por lo que los pasamos al segundo miembro:

La matriz de los coeficientes es:

Y la matriz ampliada es:

Escogemos las filas 1 y 2 y las columnas 1 y 2 para formar una submatriz cuadrada contenida en A:

Cuyo determinante es:

Que es distinto de cero, luego el rango de A es 2:

Para que el sistema tenga solución, el rango de la matriz ampliada también debe ser 2:

Por tanto, el determinante de la matriz ampliada debe ser igual a cero:

Desarrollamos el determinante en el primer miembro, dejando el segundo miembro igual a cero (lo he escrito en dos líneas):

Multiplicamos los números que quedan fuera de los paréntesis:

Y multiplicamos cada número por los términos de dentro del paréntesis para eliminarlos:

Operamos y reordenamos términos, llegando a la ecuación implícita del plano:

Que simplificando la ecuación queda:

Ejercicios propuestos sobre ecuaciones del plano

Halla la ecuación de los planos, en todas las formas posibles, determinados por las siguientes condiciones:

a) Plano que pasa por el punto P (2,-3,5) y tiene como vectores de dirección u=(1,1,2) y v=(3,-2,1)

b) Plano que pasa por los puntos P (3,-1,0) y Q (1,-1,3) y contiene al vector v=(1,2,3)

c) Plano que pasa por los puntos A (1,2,3), B (-1,0,2) y C (2,-1,0)

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS