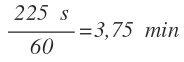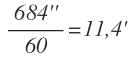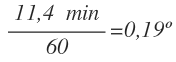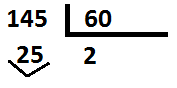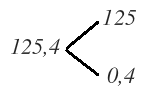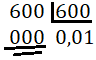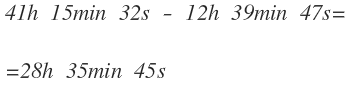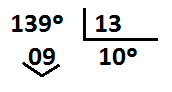A continuación te voy a explicar qué es el sistema sexagesimal y cómo podemos pasar de unas unidades a otras en su forma simple (más adelante te explicaré también qué es esto).
También te enseñaré cómo pasar de forma simple a forma compleja y de forma compleja a forma simple, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¿Qué es el sistema sexagesimal?
El sistema sexagesimal es un sistema de numeración en el que cada 60 unidades se cambia de unidad.
El tiempo y los ángulos están medidos con el sistema sexagesimal.
Las unidades de tiempo que se miden con este sistema son las horas los minutos y los segundos:
Las unidades para los ángulos son grados minutos y segundos:
Tanto las medidas de tiempo como las medidas de ángulos se pueden expresar en forma simple o en forma compleja.
Vamos a ver qué significa cada una de esas formas.
Medidas en forma simple y en forma compleja
Las medidas en forma simple son aquellas que se expresan en una sola unidad, como por ejemplo:
Las medidas en forma compleja se expresan en más de una unidad, como por ejemplo:
En esta lección, te voy a enseñar cómo pasar de unas unidades a otras en su forma simple y la forma compleja la dejaremos para la siguiente lección.
Cómo pasar de segundos a minutos
La unidad más pequeña dentro del sistema sexagesimal son los segundos, tanto como para el tiempo como para los ángulos.
60 segundos equivalen a 1 minuto, tanto para el tiempo:
Como para los ángulos:
Eso quiere decir que a partir de 60 segundos, puedo cambiar de unidad y expresarlo en minutos.
¿Cómo paso de segundos a minutos?
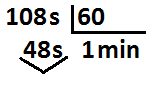
Para pasar los segundos a minutos, hay que dividir los segundos entre 60, porque estoy pasando a una unidad más grande. El resultado de la división estará en minutos.
Por ejemplo: ¿Cuántos minutos son 225 segundos?. Expresar en forma simple:
¿Cuántos minutos son 87 segundos?.Expresar en forma simple:
Podría expresar el resultado en minutos y segundos, pero eso sería en forma compleja, que lo tienes explicado en el Curso de Sistema Sexagesimal, donde puedes aprender a pasar de forma simple a forma compleja y a realizar operaciones en sl sistema sexagesimal.
¿Puedo pasar los segundos a minutos si tengo menos de 60 segundos?
Sí que se puede, pero el resultado sería un número más pequeño que 1.
Por ejemplo: ¿Cuántos minutos son 38 segundos?. Expresar en forma simple:
Como ves, el resultado es menor a 1 minuto.
Cómo pasar de minutos a horas o de minutos a grados
Como acabamos de ver, la siguiente unidad más grande que los segundos son los minutos, tanto pare el tiempo como para los ángulos.
60 minutos equivalen a 1 hora para el tiempo:
Y 60 minutos equivalen a 1 grado para los ángulos:
Lo que significa que a partir de 60 minutos, puedo cambiar de unidad y expresarlo en horas para el tiempo o en grados para los ángulos
¿Cómo paso de minutos a horas o de minutos a grados?
Para pasar los minutos a horas o a grados, hay que dividir los minutos entre 60. El resultado de la división estará en horas o en grados, según sea para el tiempo o para los ángulos
Por ejemplo: ¿Cuántas horas son 287 minutos?. Expresar en forma simple:
¿Cuántos grados son 155 minutos?. Expresar en forma simple:
¿Se pueden pasar los minutos a horas grados si tengo menos de 60 minutos?
Al igual que ocurre con los segundos, sí que se puede, pero el resultado sería un número más pequeño que 1.
Por ejemplo, ¿cuántos grados son 46 minutos?
Dividimos 46 minutos entre 60 y nos queda:
Cómo pasar de segundos a horas o de segundos a grados
Para pasar los segundos a horas, primero tengo que pasar los segundos a minutos y después esos minutos a segundos, en el caso del tiempo.
Para el caso de los ángulos sería igual: primero hay que pasar los segundos a minutos y después los minutos a grados.
Es decir, dividir entre 60 dos veces.
Por ejemplo, ¿cuantas horas serán 5268 segundos?
Primero divido los segundos entre 60 para calcular los minutos:
Y estos minutos los vuelvo a dividir entre 60 para calcular las horas:
Otro ejemplo: ¿Cuántos grados son 684 segundos?
Divido los segundos entre 60:
Y los minutos los vuelvo a dividir entre 60:
Cómo pasar de horas a minutos o de grados a minutos
Para pasar de horas a minutos, como estoy pasando de una unidad más grande a otra más pequeña, tengo que multiplicar por 60.
Por ejemplo, ¿cuántos minutos son 3 horas?
Multiplico las horas por 60 y me queda:
¿Cuántos minutos son 54º?
Para los grados hacemos lo mismo:
Cómo pasar de minutos a segundos
De la misma forma, para pasar de minutos a segundos, estoy pasando a una unidad más pequeña, por tanto, también tengo que multiplicar por 60.
Por ejemplo, ¿cuántos segundos son 15 minutos?
Multiplico los minutos por 60 y me queda:
Cómo pasar de horas a segundos o de grados a segundo
Para pasar de horas o grados a segundos, estoy pasando a una unidad dos veces más pequeña, por lo que tengo que multiplicar por 60 dos veces. Primero paso las horas a minutos y después los minutos a segundos.
Por ejemplo, ¿cuántos segundos son 4 horas?
Multiplico las horas por 60 y tengo los minutos:
Y ahora multiplico los minutos por 60 y tengo los segundos:
¿Cuántos segundos son 25º?
Primero multiplico los grados por 60 para obtener los minutos:
Y después multiplico los minutos por 60 para obtener los segundos:
Paso de medidas de forma simple a compleja
A continuación te voy a explicar cómo pasar las unidades de forma simple a forma compleja y como pasar de unas unidades a otras en forma compleja.
Cómo pasar segundos a minutos en forma compleja
Para pasar los segundos a minutos en forma compleja, dividimos manualmente los segundos entre 60. El cociente serán los minutos y el resto serán los segundos que sobran:
Vamos a ver un ejemplo: Expresar 145 segundos en minutos y segundos.
Dividimos 145 entre 60:
El resultado son 2 minutos y el resto 25 segundos, por tanto, 145 segundos son 2 minutos y 25 segundos:
Si tuviéramos menos de 60 segundos, no podemos pasarlos a minutos en forma compleja, ya que el resultado de la división sería menor que 1.
Cómo pasar minutos a horas o grados en forma compleja
Para pasar minutos a horas o grados en forma compleja, es decir, en horas y minutos, dividimos manualmente entre 60. El resultado serán las horas y el resto los minutos que sobren.
Por ejemplo: ¿Cuántos grados y minutos son 213′?
Dividimos manualmente 213 entre 60:
Me da como resultado 3, que son grados y como resto 33 minutos:
Al igual que ocurre con los segundos, para pasar los minutos a horas o grados tengo que tener más de 60 minutos
Cómo pasar minutos de forma simple a forma compleja
Vamos a ver ahora cómo pasar minutos de forma simple a forma compleja. Te lo explicaré con un ejemplo:
Expresar en forma compleja 125,4′:
En primer lugar separamos la parte entera de la parte decimal (no olvides que la parte decimal lleva delante 0,):
Si la parte entera es igual o mayor a 60 la dividimos manualmente entre 60, tal y como te expliqué más arriba. El cociente serán grados y el resto minutos.
Como tenemos 125′, vamos a dividirlo entre 60:
Por tanto, 125′ son 2º y 5′:
Si la parte entera fuera menor que 60 se quedaría tal y como está
Por otro lado nos queda la parte decimal, que la tenemos que pasar a segundos. Para ello, la multiplicamos por 60:
Por tanto, 0,4 minutos son 24 segundos, que lo tenemos que añadir al resultado de la parte entera y la medida inicial en forma compleja será:
Vamos con otro ejemplo: Expresar en forma compleja 18,95 minutos:
En primer lugar, separamos la parte entera de la parte decimal
Esta vez, la parte entera se queda tal y como está ya que es menor que 60.
Pasamos la parte decimal a segundos multiplicando por 60:
Que se lo añadimos a los 18 minutos de la parte entera y por tanto 18,95 minutos son:
Cómo pasar horas o grados de forma simple a forma compleja
Para pasar horas o grados de forma simple a forma compleja, se procede de manera similar a como acabamos de ver en el apartado anterior.
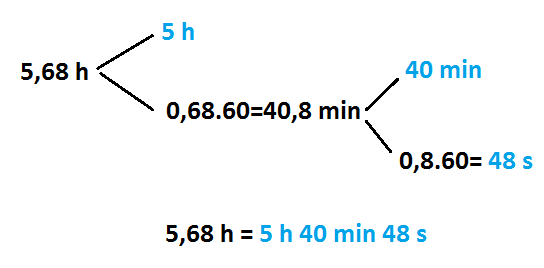
Por ejemplo: Expresar en forma compleja 5,68 h:
Separamos la parte entera de la parte decimal:
La parte entera la dejamos tal y como está. Por tanto ya tenemos 5 horas del resultado de la forma compleja.
La parte decimal, la pasamos a minutos multiplicándola por 60:
Por tanto, 5,68 horas serán igual a 5 hora y 40,8 minutos:
Ahora estos 40,8 minutos, los volvemos a pasar a forma compleja, repitiendo el proceso.
Separamos la parte entera de la parte decimal:
La parte entera la dejamos tal y como está, ya que es menor de 60 y la parte decimal la multiplicamos
Por tanto, 40,8 minutos es igual a 40 minutos y 48 segundos:
Y para finalizar, ya tenemos la cantidad inicial en forma compleja:
Te dejo aquí como resumen todos los pasos que hemos dado para pasar las horas a forma compleja:
Si quieres seguir aprendiendo todo sobre el sistema sexagesimal, te recomiendo el Curso de Sistema Sexagesimal, donde aprenderás también te explico cómo pasar medidas de forma compleja a simple y todas las operaciones en el sistema sexagesimal. Ideal para aprenderlo todo paso a paso.
Cómo pasar de forma compleja a incompleja
A continuación te voy a enseñar cómo pasar las medidas de su forma compleja a su forma simple, es decir, las que medidas que están expresadas en varias unidades, expresarlas en una sola unidad.
Paso de medidas de forma compleja a forma simple
Para pasar las medidas de forma compleja a incompleja hay que convertir cada una de las unidades en la que queremos obtener y después sumarlas.
Vamos a ir viendo varios ejemplos.
Expresar en segundos
Expresar en segundos 6h 58 min 45 s:
Primero tenemos que pasar las 6 horas a segundos, los 58 minutos a segundos, los 45 segundos ya los tenemos y sumar todos los segundos.
Para pasar las horas a segundos tenemos que multiplicar por 60 dos veces. La primera vez que multiplicamos por 60, pasamos las horas a minutos:
La segunda vez que multiplicamos por 60 convertimos los minutos que hemos obtenido en la operación anterior a segundos:
Por tanto, 6 horas corresponden a 21600 segundos:
Ahora pasamos los minutos a segundos multiplicando por 60:
Por tanto, 58 minutos corresponden a 3480 segundos:
A modo de resumen, ponemos todas las unidades juntas en segundos:
Y finalmente sumamos todos los segundos que tenemos:
Por tanto, hemos pasado la medida en horas, minutos y segundos a segundos:
Expresar en minutos
Expresar en minutos 25º 39′ 5»
Pasamos los 25º a minutos y los 5» a minutos. Y sumamos todos los minutos.
Para pasar los 25º a minutos, multiplicamos por 60:
25º corresponden a 1500′:
Para pasar los 5» a minutos, dividimos entre 60, ya que estamos pasando a una unidad mayor:
A modo de resumen, ponemos todas las unidades juntas en minutos:
Y sumamos todos los minutos que tenemos:
Por tanto, 25º 39′ 5» corresponden a 1539,08′:
Expresar en horas o en grados
Para expresar en horas o en grados cualquier medida, debes tener en cuenta que tanto los minutos como los segundos los estás pasando a una unidad mayor y tendrás que dividir por 60, dos veces en el caso de los segundos y una vez en el caso de los segundos.
Una vez tengas todo en horas o en grados, sólo tienes que sumarlos.
Vamos a ver un ejemplo: Expresar en horas 4 h 45 min 36 s:
Dividimos los 36 segundos entre 60 para pasarlos a minutos:
Como el dividendo es menor que el divisor, le añadimos un cero al dividendo y en el cociente añadimos un cero seguido de una coma decimal:
Ahora dividimos 360 entre 60:
Por tanto, 36 segundo son 0,6 minutos:
Estos 0,6 minutos los dividimos una vez más entre 60 para pasarlos a horas:
Para eliminar los decimales del dividendo, movemos un lugar hacia la derecha la coma decimal y al divisor le añadimos un cero:
Como el dividendo es más pequeño que el divisor, añadimos 2 ceros al dividendo y como consecuencia, en el cociente añadimos 0,0:
Ahora dividimos 600 entre 600:
Por tanto, 0,6 minutos equivalen a 0,01 horas:
Ahora vamos a pasar los 45 minutos a horas. Para ellos dividimos entre 60:
Como 45 es menor que 60, le añadimos un cero a 45 y en el cociente añadimos 0,:
Ahora dividimos 450 entre 60. Obtengo 2 decimales en el cociente ya que ha visto que el resto de la división iba a ser cero:
Por tanto, 45 minutos equivalen a 0,75 horas;
Por último sumamos las horas de cada unidad y nos queda:
Si quieres aprender a trabajar con el sistema sexagesimal, te recomiendo el Curso de Sistema Sexagesimal. Échale un vistazo a sus lecciones.
Operaciones en el sistema sexagesimal. Ejercicios resueltos
A continuación voy a explicarte cómo operar en el sistema sexagesimal con medidas en forma compleja. Aprenderás a sumar, restar, multiplicar y dividir en el sistema sexagesimal.
Cómo sumar en el sistema sexagesimal
Vamos a realizar la siguiente suma:
En primer lugar sumamos los grados con los grados, los minutos con los minutos y los segundos con los segundos, colocando una medida debajo de otra y colocando el resultado debajo de ellas:
Si lo segundos suman más de 60, hay que pasarlos a forma compleja, es decir, a minutos y segundos, dividiéndolos entre 60. El cociente serán minutos y el resto serán segundos.
En nuestro caso, tenemos 81», que suman más de 60, por lo que los pasamos a forma compleja dividiendo entre 60:
Y nos queda:
El minuto se lo sumamos a los 83 minutos que ya teníamos:
Y los 21 segundos forman parte del resultado final, que ahora es éste, después de realizar el cambio:
No ha variado, tan solo hemos pasado los segundos a minutos y segundos para no tener más de 60 segundos.
Si tenemos más de 60 minutos hay que hacer lo mismo que hemos hecho con los segundos, es decir, pasarlos a forma compleja (horas y minutos) dividiendo entre 60.
En nuestro caso tenemos 84′, por lo que los dividimos entre 60. El cociente serán grados y el resto serán minutos:
Por tanto, 84′ son igual a 1º y 24′:
El grado se lo sumamos a los 51º que ya teníamos:
Y los 24 minutos formarán parte del resultado, que nos queda:
Por tanto, la suma de las dos medidas en forma compleja con su resultado es:
Cómo restar en el sistema sexagesimal
Ahora vamos a ver cómo se resta en el sistema sexagesimal. Vamos a realizar la siguiente resta:
Colocamos las medidas verticalmente para realizar la resta y ponemos cada unidad debajo de la misma unidad: las horas debajo de las horas, los minutos debajo de los minutos y los segundos debajo de los segundos:
Recuerda que cuando realizamos una resta, la cantidad que se coloca arriba se llama minuendo y la que se coloca debajo se llama sustraendo.
Te recuerdo esto para poder referirme a cada medida mientras te voy explicando cómo restar en el sistema sexagesimal.
Empezamos restando los segundos.
Si no es posible porque los segundos del minuendo son menores que los segundos del sustraendo, en el minuendo, se convierte uno de los minutos en 60 segundos y se suman a los segundos que ya tiene. Con esto se consigue que los segundos del minuendo sean mayores que los segundos del sustraendo.
En nuestro caso, a 32 segundos no podemos restarle 47 segundos. Por tanto, vamos a coger uno de los minutos del minuendo y lo vamos a convertir en segundos.
Para ello, de los 15 minutos que tenemos, le restamos 1:
Ese minuto que hemos restado lo pasamos a segundos:
Y se lo sumamos a los 32 segundos que ya teníamos:
Por lo que la medida me queda de la siguiente manera (con 1 minuto menos y 60 segundos más, que al fin y al cabo es lo mismo):
Colocamos la nueva medida transformada en el minuendo y ahora sí, procedemos a restar los segundos:
Seguimos restando los minutos.
Si la cantidad de minutos del minuendo son menores que la cantidad de minutos del sustraendo, tenemos que hacer algo similar que hemos hecho con los segundos, es decir, en el minuendo, tenemos que convertir una de las horas en 60 minutos y sumar esos 60 minutos a los que ya tenemos.
Al hacerlo así, tendremos más minutos en el minuendo que en el sustraendo y podremos restarlos.
En nuestro caso, no podemos restar 39 minutos a 14 minutos, por tanto, vamos a coger una de las 41 horas, las vamos a pasar a minutos y se las vamos a sumar a los 14 minutos que tenemos.
Para ellos, de las 41 horas que tenemos, le restamos 1:
Esa hora, la pasamos a minutos:
Y esos 60 minutos se los sumamos a los 14 minutos que ya tenemos:
Por lo que la medida transformada queda con una hora menos y 60 minutos más:
Colocamos la nueva medida en el minuendo de la resta, y ahora sí, ya se pueden restar los minutos:
Y finalmente restamos las horas:
La resta de las dos medidas en forma compleja con su resultado es:
Cómo multiplicar una medida sexagesimal por un número
Te voy a explicar ahora cómo multiplicar una medida sexagesimal por un número, con este ejemplo:
Multiplicamos las horas, los minutos y los segundos independientemente por el número:
Y procedemos igual que en la suma. Si la cantidad de segundos son más de 60, hay que pasarlos a forma compleja, es decir, a minutos y segundos, dividiéndolos entre 60. El cociente serán minutos y el resto serán segundos.
En nuestro caso, tenemos 108 segundos, por lo que los pasamos a forma compleja dividiendo entre 60:
Que nos queda:
El minuto se lo sumamos a los 136 minutos que ya teníamos:
Y los 48 segundos pasan a formar parte del resultado final, que ha quedado así:
Si tenemos más de 60 minutos, tenemos que pasarlos a forma compleja, dividiendo entre 60. Como tenemos 137 minutos, los pasamos a forma compleja (horas y minutos) dividiendo entre 60:
Que nos queda:
Los 17 minutos forman parte del resultado final y las 2 horas se las sumamos a las 24 horas que ya teníamos:
Y el resultado final queda así:
Por tanto, la multiplicación de la medida sexagesimal por el número, con su resultado es:
Como dividir una medida sexagesimal entre un número
Para terminar, te voy a explicar cómo dividir una media sexagesimal entre un número, con este ejemplo:
Empezamos dividiendo entre 13 manualmente los grados:
El cociente forma parte del resultado y el resto hay que multiplicarlo por 60 para pasarlo a minutos:
Se suman estos minutos a los 46 que ya tenemos:
Y estos 596 minutos son los que se dividen entre 13:
El cociente forma parte del resultado y el resto hay que multiplicarlo por 60 para pasarlo a segundos:
Se los sumamos a los 16» que ya tenemos:
Y estos segundos son los que se dividen entre 13:
En este caso ya no se divide manualmente porque el resto ya no podemos seguir pasándolo a otra unidad más pequeña.
Por tanto, la división de la medida sexagesimal entre el número con su resultado es:
¿Quieres profundizar más? Te recomiendo el Curso de Sistema Sexagesimal. Explicaciones más detalladas y con ejercicios propuestos para resolver.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: