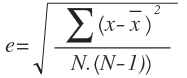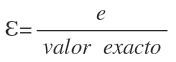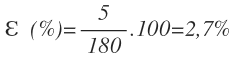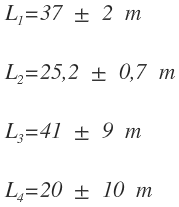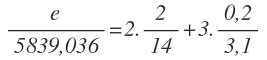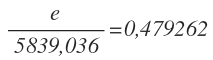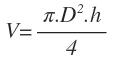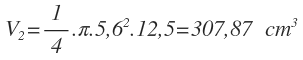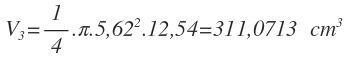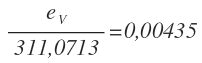Los errores absolutos y relativos son dos tipos de errores experimentales ¿Cuál es la diferencia entre ellos y cómo se calculan?
Es lo que vamos a ver a continuación, pero antes, tenemos que aprender un poco más sobre los errores en las medidas.
Si has llegado hasta aquí es porque buscas ayuda para resolver algún problema de física y necesitas clases de física online y es muy probable que también necesites refuerzo en matemáticas. Si después de leer esto, quieres seguir aprendiendo paso a paso, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Física Online:
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas y física. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus problemas de física
En este vídeo tienes explicados cómo calcular el error absoluto y el error relativo con ejercicios resueltos paso a paso:
https://youtu.be/FB8FWO8ze0o
Y a continuación tienes todo explicado más despacio:
Error en las medidas
En cualquier medición que se realice, siempre se cometen errores. Estos errores pueden provenir de dos fuentes: errores sistemáticos y los aleatorios o accidentales.
Los errores sistemáticos son los debidos al aparato de medida y se pueden corregir utilizando instrumentos adecuados. Para que un aparato sea adecuado, tiene que se fiel, exacto y preciso:
- Un aparato es fiel cuando al medir el mismo objeto varias veces, el resultado es el mismo
- Un aparato es exacto cuando el resultado obtenido coincida con el valor real
- Un aparato es preciso cuando es capaz de medir pequeñas variaciones de una magnitud.
Los errores aleatorios o accidentales, son los debidos a la persona que está realizando la medición. Estos errores se dan por defecto y por exceso. Para reducirlos, se realizan repetidas mediciones y se utiliza como valor exacto el valor medio.
Por tanto, todas las medidas están afectadas por un error experimental y es por eso que la medición va acompañada por una incertidumbre, que es un valor que se obtiene gracias al cálculo del error absoluto y el error relativo:
Error absoluto
El error absoluto se define como la diferencia entre el valor real y el valor aproximado, en valor absoluto:
donde:
- El valor real es el valor que en teoría mide la magnitud a medir
- El valor aproximado es la media de las diferentes medidas
Este valor del error absoluto es el debido a la persona que realiza la medición. Además, está el error debido a la precisión del instrumento de medida, que coincide con la unidad más pequeña con la que puede medir el aparato.
El error absoluto será el mayor valor entre el error del medidor y el error del aparato.
El error absoluto se mide en las mismas unidades que la medición.
Además, se expresa siempre con una cifra distinta de cero, redondeándose siempre en exceso. Es decir, no podemos expresar el error absoluto de esta forma:
Sino que el 0,018 debemos redondearlo a 0,02:
Por otro lado, error no puede ser más precisa (en decimales) que el error. Deben ser igual de precisas. Si el error está expresado en centésimas, la medición no puede ir expresada en unidades:
Sino que la medición debe ir también expresada en centésimas:
Si la medición es un número entero, entonces para llegar a las centésimas añadiríamos ceros después de la coma.
Ejemplo de cálculo de error absoluto
Una barra de metal mide 10 metros de largo. La medimos con un metro calibrado en milímetros y nos da una medición de 9,998 metros. ¿Cuál es el error absoluto?
En nuestro caso, el metro mide en milímetros, luego el error del aparato es:
El error debido a la persona que realiza la medición es la diferencia entre el valor real y el valor aproximado:
En este caso el valor es 10 m y el valor aproximado es 9,998 m, que es el valor obtenido, por lo que el error es:
Una vez obtenidos el error del aparato y el error del medidor, el error absoluto es el mayor de los dos:
Observa como tanto la medida como el error están expresados en milésimas y el error sólo tiene una cifra distinta de cero.
Cálculo del error absoluto en medidas directas
Vamos a ver ahora cómo calcular el error absoluto cuando se realizan varias medidas directas.
En este caso debemos utilizar la siguiente fórmula:
Donde en el numerador tenemos la suma del cuadrado de cada dato medido menos el valor medio de los datos y en el denominador N es el número de datos.
Por ejemplo:
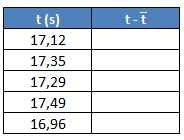
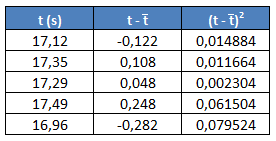
En un experimento tomamos las siguientes medidas de tiempo. ¿Cuál es el error absoluto de la medida?:
En primer lugar, calculamos la media de las mediciones, que será el valor exacto de la medición. Para ello, sumamos todos los valores y dividiendo entre el número de mediciones, que en este caso es 5:
Calculamos y nos queda:
Por tanto, este valor de 17,242 s, lo consideraremos el valor exacto de la medición.
Vamos a calcular el error absoluto de la medición aplicando la siguiente fórmula:
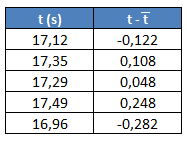
Empezamos calculando la suma del numerador. Para ello, añadimos una columna a la tabla de datos, donde a cada valor le restaremos la media:
Por ejemplo, para el primer dato de 17,12 s, este cálculo nos queda:
Lo hacemos igual para el resto de valores y lo vamos escribiendo en esta columna:
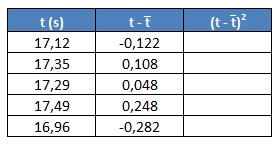
Después añadimos otra columna donde elevamos los valores obtenidos en la segunda columna al cuadrado:
Por ejemplo, para el primer valor de la segunda columna sería:
Lo hacemos igual para el resto de datos:
Estamos buscando la suma del valor de cada dato menos la media al cuadrado, por tanto, para obtenerlo, sólo tenemos que sumar todos los valores de la tercera columna:
Sustituimos este valor en la fórmula, N lo sustituimos por 5, que es el número de datos que tenemos y calculamos:
Este error absoluto corresponde al error del medidor:
El valor del error absoluto debe tener sólo una cifra distinta de cero y reondearse por exceso, por lo que redondeamos a 0,1:
Por otro lado, debemos obtener el error del aparato, que es igual a la unidad más pequeña con la que puede medir el instrumento de medida. En nuestro caso el error del aparato es 0,01, ya que hemos podido medir hasta centésimas de segundo:
El error absoluto es el mayor entre el error del medidor y el error del aparto. Como el mayor es el error del medidor nos quedamos con el valor de 0,1 s para el error absoluto.
La medida final la expresamos como el valor exacto, que era la media de las medidas con su error absoluto:
Como el valor de la medición y el error deben tener la misma precisión (mismo número de decimales), ajustamos el valor exacto a los decimales del error, por lo que nos queda que el valor final de la medición es:
Error relativo
El error relativo se calcula dividiendo el error absoluto entre el valor exacto:
El error relativo se mide en porcentaje, luego para obtener directamente el error en tanto por ciento, a la expresión anterior hay que multiplicarla por 100:
El error relativo lo utilizamos para determinar la precisión de la medición. Nos dice la proporción del error con respecto al valor exacto de la medición. Una medida es buena cuando no supera el 5%.
Ejemplo de error relativo
Vamos a ver un ejemplo de cálculo de error relativo:
Queremos medir 180 cm³ de agua con una probeta con un error relativo menor del 3%. ¿Bastará con una probeta graduada de 5 en 5 cm³ o necesitaremos una que vaya de 2 en 2 cm³?
El valor exacto de la medida es 180 cm³. Con la probeta graduada de 5 en 5 cm³, tenemos un error del aparato de 5 cm³, que es el error absoluto de la medición en este caso, por lo que la medida con su error nos queda:
Vamos a calcular el error relativo para este caso con la fórmula:
Sustituimos el error absoluto y el valor exacto y calculamos:
El valor relativo que obtenemos es de 2,7%, que es menor de 3%, por lo que la probeta graduada de 5 en 5 cm³ nos valdría.
Vamos a ver el caso de la probeta graduada de 2 en 2 cm³. En este caso la medida con su error absoluto es:
Calculamos su error relativo:
El error relativo es todavía más bajo que en el caso anterior, ya que tenemos más precisión en la medida.
Por tanto, cualquiera de las dos probetas nos valdría y con la segunda obtenemos una mayor precisión.
Cálculo del error absoluto en medidas indirectas
Veamos cómo calcular el error absoluto cuando las medidas con indirectas, es decir, se obtienen haciendo operaciones a partir de otras medidas tomadas directamente.
Se distinguen dos casos:
- Cuando en la expresión matemática sólo aparecen sumas y restas, el error absoluto es la suma de los errores absolutos de las medidas directas.
- Cuando en la expresión matemática aparecen productos, divisiones y potencias, el error relativo del producto es la suma de los errores relativos de las diferentes magnitudes implicadas, multiplicadas por sus exponentes.
Vamos a ver un ejemplo de cada uno de los casos.
Cómo calcular el error absoluto en medidas indirectas cuando sólo aparecen sumas y rectas
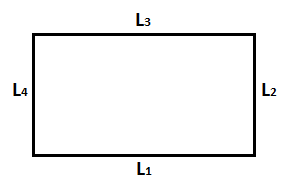
Calcular el perímetro del siguiente rectángulo:
Sabiendo que las medidas de sus lados son:
El perímetro de este rectángulo es:
Para calcular el valor exacto del perímetro sumamos los valores de las medidas:
Para calcular el error absoluto del perímetro, sumamos los valores de los errores absolutos:
El error absoluto sólo puede tener una cifra distinta de cero, por lo que redondeamos por exceso:
El valor del perímetro con su error es:
Como la medida y el error deben tener la misma precisión, ajustamos el número de decimales del valor de la medida al número de decimales del error (ninguno) y redondeamos (en este caso no es necesario que sea siempre por exceso).
El valor de final del perímetro es:
Cómo calcular el error absoluto en medidas indirectas cuando aparecen productos, divisiones y potencias
Supongamos que queremos calcular el valor de M junto con su error y que M se calcular mediante la siguiente expresión:
Los valores de l y de t son:
En primer lugar calculamos M con los valores exactos de l y t:
Ahora vamos a calcular el error absoluto de M. Como en la expresión para calcular M aparecen productos, sabemos que el error relativo de M es igual al error relativo de l, multiplicado por su exponente, más el error relativo de l multiplicado por su exponente:
Por otro lado, sabemos que el error relativo es igual al error absoluto dividido por el valor exacto:
Sustituimos esta última expresión en cada uno de los errores relativos. En el caso del error relativo de M, no conocemos su valor absoluto, puesto que es lo que queremos calcular, y lo dejamos como incógnita:
Operamos en el segundo miembro:
Pasamos el denominador del primer miembro multiplicando al segundo miembro y calculamos:
Redondeamos el error absoluto por exceso:
El valor de M con su error es:
Finalmente, ajustamos el número de decimales del valor de la medida al número de decimales del error y redondeamos:
Vamos a ver otro ejemplo de cómo calcular el error absoluto en medidas indirectas:
Tres estudiantes determinan el volumen de un mismo cilindro. El primero lo hace directamente y obtiene una medida de 308 ± 4 cm³. El segundo lo hace midiendo el diámetro de la base y la altura con una regla y después calculando el volumen con la fórmula V=(π.D².h)/4. Las medidas que obtiene son h=12,5 ± 0,1 cm y D=5,6 ± 0,1 cm. El tercero también utiliza la fórmula del volumen pero utiliza un calibre para tomar medidas. Las medidas que obtiene son h=12,54 ± 0,01 cm y D=5,62 ± 0,01 cm. Hallar los tres volúmenes.
El volumen del primer alumno ya lo tenemos puesto lo obtiene directamente:
El segundo alumno obtiene las siguientes medidas:
Utiliza la siguiente fórmula para calcular el volumen:
Para poder utilizar la expresión de los errores relativos, es necesario que tengamos un producto de factores. Para ello, en vez de dividir entre 4, lo que hacemos es convertir el denominador en la fracción 1/4, que multiplique al resto de factores:
Calculamos el valor exacto de V con los valores de las medidas de h y de D:
El error absoluto lo calculamos a partir de los errores relativos. El error relativo del volumen será igual a la suma de los errores relativos de cada uno de los factores, multiplicados por su exponente:
El error relativo de 1/4 y el error relativo de π se consideran despreciables y por tanto son igual a 0. El resto de errores relativos los sustituimos por los errores absolutos entre el valor exacto, quedando como incógnita el error absoluto del volumen:
Operamos en el segundo miembro:
Pasamos el denominador del primer miembro multiplicando al segundo miembro y calculamos:
Redondeamos el valor del error absoluto por exceso:
La medida del volumen del segundo alumno con su error es:
Finalmente redondeamos el valor de la medida para que tenga la misma precisión que el error:
El tercer alumno obtiene las siguientes medidas:
Utilizamos la siguiente fórmula para calcular el volumen:
Sustituimos valores y calculamos el valor exacto del volumen:
Igual que antes, utilizamos los errores relativos para calcular el error absoluto:
Sustituimos los errores relativos por el error absoluto entre el valor exacto:
Operamos en el segundo miembro:
Y pasamos el denominador del primer miembro multiplicando al segundo miembro:
Redondeamos el error absoluto por exceso:
El valor del volumen con su error es:
Finalmente, redondeamos el valor exacto para que tenga la misma precisión que el error:
¿Necesitas ayuda en física y matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar.
He diseñado un método práctico y efectivo que te ayudará a entender la física así como las matemáticas que necesitas aplicar, paso a paso, explicándote justo lo que necesitas para saber resolver todos problemas y saber aplicar las fórmulas que correspondan. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus problemas de física
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender física y las matemáticas que necesitas aplicar. ¿Quieres informarte de como puedes aprender física y matemáticas? Pulsa el botón para saber más: