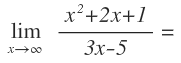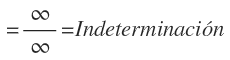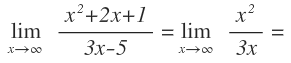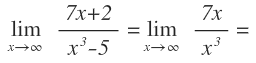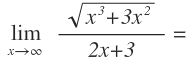A continuación te voy a explicar cómo resolver la indeterminación infinito entre infinito en el cálculo de límites.
Normalmente, para resolver el límite, tan sólo tenemos que sustituir la x por el valor al que tiende.
No obstante hay veces que nos encontramos con que al sustituir, el resultado sea una indeterminación y en ese caso, debemos utilizar el método de cálculo que corresponda en cada caso.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Cómo calcular límites con indeterminaciones del tipo infinito entre infinito. Ejercicios resueltos.
Este tipo de indeterminación lo encontramos en los límites de cuando x tiende a infinito (o menos infinito) de funciones racionales y al sustituir nos queda ∞/∞.
En general son tienen esta forma:
Cuando tengamos la indeterminación de límites infinito entre infinito, tenemos que eliminar términos del numerador y del denominador y dejar sólo los términos de mayor grado arriba y abajo.
Una vez lo tenemos los términos de mayor grado, podemos operar y eliminar las x que se repitan tanto en el numerador como en el denominador.
Al operar, la indeterminación desaparece y debemos sustituir de nuevo la x por el número al que tiende para llegar al resultado.
Para resolver y entender muy bien este tipo de indeterminaciones es importantes dominar tanto los polinomios como las fracciones algebraicas. Si no es tu caso, antes de seguir te aconsejo hacer el Curso de Polinomios y el Curso de Fracciones Algebraicas.
Vamos a ir viéndolo paso a paso con varios ejercicios resueltos como ejemplo. Empezamos con este límite:
Todos los límites empiezan resolviéndose igual: sustituyendo la x por el número al que tiende, es decir, no se resuelve sabiendo antes de empezar que va a ser una indeterminación. Eso no tenemos por qué saberlo.
Una vez hemos sustituido la x y operando, entonces podemos llegar a un resultado concreto o llegar a la conclusión de que es una indeterminación.
En primer lugar, sustituimos la x por infinito y nos queda una indeterminación:
Para resolver este tipo de indeterminación dejamos en el numerador y en el denominador sólo el término de mayor grado:
Una vez hemos dejado el término de mayor grado, operamos y eliminamos los factores que se repitan tanto en el numerador como en el denominador. En este caso, podemos eliminar una x en cada lado:
Y finalmente, hemos sustituido otra vez la x por infinito, pero esta vez, ya no tenemos ninguna indeterminación y el resultado es infinito entre un número, que es igual a infinito.
Vamos a ver otro ejemplo:
Empezamos sustituyendo la x por infinito y nos queda:
Esta vez tenemos un infinito negativo en el denominador, pero sigue siendo el mismo tipo de indeterminación.
Dejamos el término de mayor grado en el numerador y el denominador:
Operamos eliminando una x del numerador y otra del denominador y sustituimos otra vez la x por infinito, llegando al resultado de menos infinito, ya que estamos dividiendo por un número negativo:
Seguimos con otro ejemplo:
Sustituimos la x por infinito y llegamos a la indeterminación infinito entre infinito:
Dejamos el término de mayor grado en el numerador y en el denominador:
Operamos y podemos eliminar una x tanto en el numerador como en el denominador. Esta vez en el numerador no tenemos ninguna x, por lo que a la hora de sustituir, el infinito nos queda sólo en el denominador y por tanto, un número entre infinito, da como resultado cero:
Vamos a terminar la indeterminación infinito partido por infinito con este ejemplo:
Sustituimos la x por infinito y queda la indeterminación infinito partido por infinito:
Dejamos el término de mayor grado arriba y abajo:
Al operar, podemos eliminar x elevado al cuadrado tanto en el numerador como en el denominador, por lo que desaparecen las x. Por tanto, a la hora de volver a sustituir la x por infinito, como no tenemos x, el resultado es el mismo número que nos ha quedado:
Indeterminación infinito entre infinito con raíces
Cuando nos encontramos radicales en los límites suele causar confusión. Vamos a ver cómo resolverlos si tenemos la indeterminación de infinito entre infinito con raíces.
Por ejemplo:
Sustituimos la x por infinito y llegamos a la conclusión de que es una indeterminación:
Nos quedamos con el término de mayor grado, pero ahora hay que tener cuidado con los radicales. En el numerador, el término de mayor grado es el primero, ya que el segundo término está dentro de otra raíz y por tanto el grado es menor.
En el denominador, el término de mayor grado es el de la raíz.
Nos queda por tanto el mismo término arriba y abajo:
Al operar, nos queda que la función es igual a 1, ya que ambos términos se pueden dividir entre sí, y por tanto, el límite de la función cuando x tiende a infinito es igual a 1:
Vamos a ver otro ejemplo:
Sustituimos la x por infinito y nos queda la indeterminación de infinito partido por infinito
Dejamos el término de mayor grado en el numerador y en el denominador:
Y ahora tenemos que operar, pero no se ve tan claro cómo operar para eliminar una de las x, como en el resto de ejemplos que hemos visto.
En primer lugar la raíz la pasamos a exponente fraccionario:
Y ahora, para operar con las x las consideramos como una división de potencias de la misma base, donde mantenemos la x y restamos los exponentes:
Y nos queda una sola x en el numerador, que al sustituir por infinito, el resultado es infinito:
Conclusión de la indeterminación infinito entre infinito
Con la indeterminación de infinito entre infinito, el resultado va a depender del grado de los polinomios del numerador y del denominador:
- Si el grado de P(x) es menor que el grado de Q(x) el resultado va a ser cero
- Si el grado de P(x) es mayor que el grado de Q(x) el resultado va a ser infinito o menos infinito
- Si el grado de P(x) es igual que el grado de Q(x) el resultado va a ser un número
En los ejemplos resueltos que hemos ido resolviendo a lo largo de la lección, hemos visto al mismo tiempo cada uno de los casos.
¿Necesitas clases de matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: