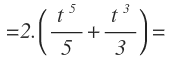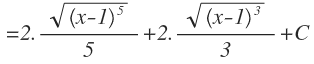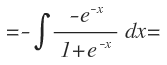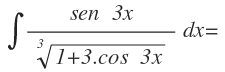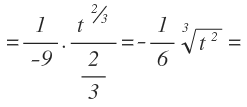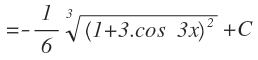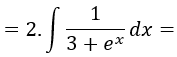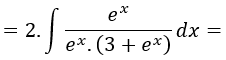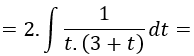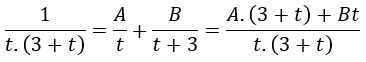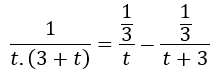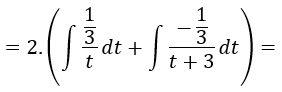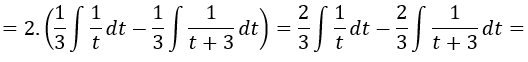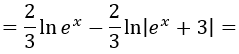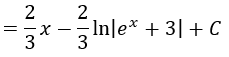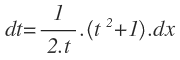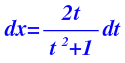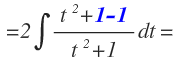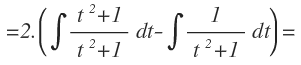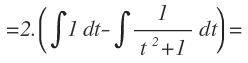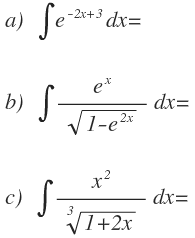Integración por sustitución o cambio de variable. Ejercicios resueltos.

A continuación te voy a enseñar cómo integrar por el método de sustitución o de cambio de variable, con ejercicios resueltos paso por paso.

Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Cómo resolver integrales por sustitución

Las integrales que se resuelven por el método de sustitución o cambio de variable no siguen ninguna metodología establecida.

Se realiza un cambio de variable para simplificar la integral y facilitar su resolución, que generalmente llamaremos t. Se resuelve la nueva integral en función de la nueva variable t y una vez resuelta, se vuelve a cambiar la variable t por su expresión en función de la variable x.

Una buena forma de aprender a resolver integrales por sustitución es practicando, lo que hará que deduzcas antes cuál es el cambio de variable a realizar, por haber realizado otra integral similar.

Ejercicios resueltos de integrales por sustitución

Vamos a resolver unas cuantas integrales por sustitución paso por paso

Integral por sustitución 1

En general, cuando tengamos una raíz en una integral, realizamos el cambio de variable con el contenido de la raíz o bien toda la raíz. En este caso, el cambio de variable es:

de donde podemos despejar la x:

Y en esta última expresión derivamos en ambos miembros:

(el cambio t=x-1 también es posible)

Como ves, una vez hecho el cambio de variable, tenemos que buscar la forma para poder poner todos los factores que aparecen en la integral en función de la nueva variable.

Ahora sustituimos los factores de la integral por los nuevos factores en función de x:

Operamos y sacamos fuera la constante:

Integramos aplicando el método de integrales inmediatas:

Operamos para eliminar el paréntesis:

Y finalmente, volvemos a cambiar la variable «t» por su expresión en función de x y le añadimos la constante:

Integral por sustitución 2

En este caso, la nueva variable es igual a e elevado a -x:

En esta expresión, derivamos en ambos miembros:

Para poder sustituir dt en la integral, necesitamos un signo menos, que se lo añadimos y se lo quitamos:

Sustituimos todos los factores por los nuevos en función de «t»:

Integramos por medio de integrales inmediatas:

Volvemos a sustituir la t por su expresión en función de x y le añadimos la constante:

Integral por sustitución 3

En este caso, la nueva variable será igual al contenido de la raíz:

Y en esta expresión derivamos en ambos miembros:

Para poder sustituir dt en la integral necesitamos un -9, que se lo añadimos y se lo quitamos:

Sustituimos todas las variables en función de x por su correspondiente expresión en función de t y ponemos la raíz en su forma exponencial:

Integramos aplicando integrales inmediatas y volvemos a dejar el resultado en forma de raíz:

Finalmente, volvemos a sustituir la «t» por su expresión en función de x:

Integral por sustitución 4

Sacamos la constante fuera de la integral:

Ahora realizamos el cambio de variable. La nueva variable es igual a e elevado a x:

Derivamos en ambos miembros:

Para poder sustituir dt en la integral, necesitamos un signo menos, nos falta un e elevado a x, por lo que se lo añadimos al numerador y para no alterar la función, lo añadimos también en el denominador:

Sustituimos todas las variables en función de x por su correspondiente expresión en función de t:

Nos ha quedado una integral racional con raíces reales distintas en el denominador, que pasamos a resolver.

Descomponemos la función racional en una suma de fracciones simples:

Sustituimos la función racional de la integral por la suma de fracciones simples:

Operamos:

Resolvemos la integral:

Una vez resuelta la integral, sustituimos t por su expresión en función de x (deshacemos el cambio de variable):

Y por último, operamos en el primer término y añadimos la constante:

Integral de la raíz de e elevado a x menos 1

La resolución de la integral de la raíz de e elevado a x menos 1 es bastante compleja ya que no es nada intuitiva.

Empezamos realizando el cambio de variable igual a la raíz de e elevado a x menos 1 (la dejo en azul porque la necesitaremos más adelante):

De esta expresión podemos despejar e elevado a x:

Por otro lado, en la primera expresión derivamos en ambos miembros:

Nos ha quedado una expresión en la que volvemos a tener la raíz de e elevado a x menos 1 y además tenemos otro e elevado a x. Ambos los podemos sustituir en función de t, gracias a las dos expresiones anteriores:

Y de esta última ecuación, podemos despejar dx para tenerlo en función de t (que también la dejo en azul):

Con las expresiones que tenemos para expresar la raíz de e elevado a x menos 1 y dx en función de t (ambas en color azul), realizamos la sustitución en nuestra integral:

Sacamos fuera la constante y operamos:

Vemos que el denominador es perfecto para aplicar la fórmula de la integral inmediata del arco tangente, pero no así el numerador.

No obstante, si en el numerador sumamos 1 y lo volvemos a restar para no alterar el resultado de la función:

Podemos separar la integral en dos nuevas integrales:

Una de las cuales el numerador y el denominador se anula y la otra queda preparada para resolverla con la fórmula de la integral inmediata del arco tangente:

Integramos:

Operamos para eliminar el paréntesis:

Y finalmente volvemos a sustituir la «t» por su expresión en función de x y le añadimos la constante:

Ejercicios propuestos

Resuelve las siguientes integrales:

¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS