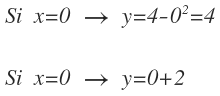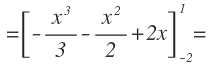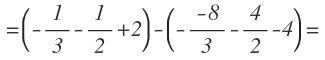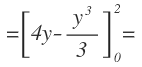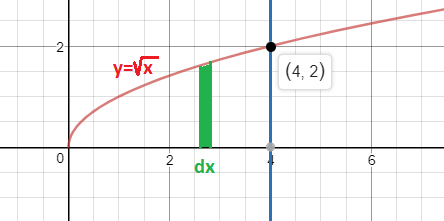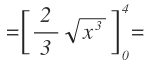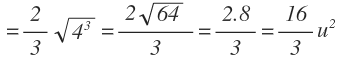A continuación te voy a explicar cómo calcular áreas mediante integrales iteradas dobles. Veremos cómo calcular áreas dependiendo del orden de integración elegido, con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Tienes disponibles el Curso de Integración Múltiple donde además te explico con todo detalle cómo calcular volúmenes o cómo calcular integrales triples, por ejemplo.
¡Vamos allá!
Calcula áreas con integrales iteradas dobles con el orden de integración dy.dx
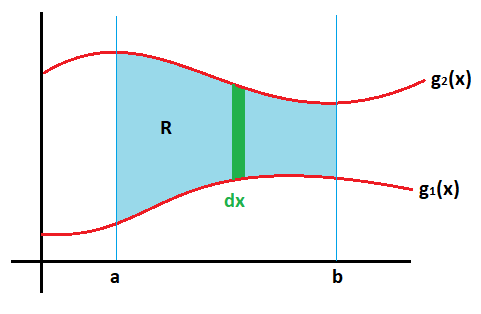
Vamos a considerar una región plana R acotada por:
Que representada gráficamente queda:
Esta región R está compuesta por infinitos rectángulos dx, representados como un rectángulo vertical:
Este rectángulo vertical dx tiene dos características muy importantes:
- Se mueve horizontalmente entre los límites de x a y b.
- En función de su posición, va variando su altura adaptándose a las funciones g2(x) y g1(x), quedando siempre dentro de ambas funciones, por lo que su altura está limitada superiormente por la función que de arriba g2(x) e inferiormente por la función de abajo g1(x).
Por tanto, con este rectángulo podemos deducir los límites integración para la variable x, que son los dos límites entre los que se puede desplazar el rectángulo horizontalmente, por tanto, es por eso que el área de esa región viene dada por la integral definida:
Por otro lado, podemos reescribir el integrando g2(x)-g1(x) como una nueva integral definida, pero integrada para la variable «y».
Vamos a ver cómo.
Los límites de esta integral están determinados por la altura del rectángulo dx, es decir entre las funciones g2(x) y g1(x) y al ser «y» la variable de integración, el diferencial en este caso es dy:
Resolvemos esta integral utilizando la regla de Barrow y nos queda:
Por tanto, sustituyendo en la integral definida anterior el integrando g2(x)-g1(x), por la integral con respecto a «y», el área de la región R se puede expresar como la integral iterada:
El rectángulo vertical, implica el orden de integración dy.dx.
Calcula áreas con integrales iteradas dobles con el orden de integración dx.dy
Análogamente, podemos calcular el área de una región cambiando el orden de integración a dy.dx.
En este caso, la región R está delimitada por:
Date cuenta de que ahora, las funciones entre las que está limitada la variable x, depende de «y».
Y al igual que antes, esta región R está compuesta por infinitos rectángulos, pero esta vez los rectángulos son horizontales y corresponden a dy. Por tanto, dy se representa como un rectángulo horizontal:
Este rectángulo horizontal dy tiene dos características muy importantes:
- Se mueve verticalmente entre los límites de «y» c y d.
- En función de su posición, va variando su longitud adaptándose a las funciones h2(y) y h1(y), quedando siempre dentro de ambas funciones, por lo que su longitud está limitada superiormente por la función que de arriba h2(y) e inferiormente por la función de abajo h1(y).
Por tanto, con este rectángulo podemos deducir los límites integración para la variable y, que son los dos límites entre los que se puede desplazar el rectángulo verticalmente.
Los límites de integración para la variable x están determinados por la longitud del rectángulo, es decir, por ambas funciones.
En este caso, el área de la región R se puede expresar como la integral iterada:
El rectángulo horizontal, implica el orden de integración dx.dy..
Integrales iteradas dobles para el cálculo de áreas
En resumen, si queremos calcular el valor del área de una región en el plano mediante una integral iterada, está vendrá dada por:
1- Si R está definida por:
donde g1 y g2 son contínuas en [a,b], entonces el área de R será:
2- Si R está definida por:
donde h1 y h2 son contínuas en [c,d], entonces el área de R será:
¿Cómo sabemos qué integral iterada utilizar para el cálculo de áreas?
Cuando las funciones entre las que se define el área vienen dadas en función de x, el rectángulo representativo del área será vertical y por tanto el orden de integración será dy.dx.
Por otro lado, si las funciones vienen dadas en función de «y», el rectángulo representativo será horizontal y el orden de integración será dy.dx.
No obstante, podemos cambiar el orden de integración modificando los límites de la región.
Para cada problema en concreto, uno de los dos órdenes hará más sencillos los cálculos. El orden de integración elegido afecta a la dificultad de los cálculos, pero no al resultado. En cada caso, se elige el orden de integración más conveniente.
Vamos a verlo con unos ejercicios resueltos
Ejercicios resueltos de cálculo de áreas con integrales iteradas dobles
Ejercicio resuelto 1
Calcular el área delimitada por estas dos funciones mediante una integral iterada doble:
Como las funciones estás definidas en función de x, vamos a utilizar el orden de integración dy.dx
En primer lugar, vamos a calcular los puntos de corte de estas dos funciones, ya que los puntos de corte serán los límites de integración de al variable x, es decir, los límites entre los cuales se mueve horizontalmente el rectángulo vertical dx.
Para hallar los puntos de corte, igualamos las dos funciones:
Nos queda una ecuación de segundo grado, por lo que pasamos todos los términos a un miembro e igualamos a cero:
Simplificamos términos:
Y resolvemos la ecuación. Las soluciones son:
Por lo que los límites para dx son -2 y 1. Siempre ponemos en el límite inferior el número menor y en el límite superior el límite mayor.
Los límites para la variable «y», están definidos por la altura del rectángulo, que se mueve entre las dos funciones. La función que quede arriba será el límite superior y la que quede abajo el límite inferior.
Para saber esto podemos dibujar ambas funciones:
Vemos que queda por encima la función:
Por lo que ésta será la que determine el límite superior y la otra función la que determine el límite inferior.
También podemos sustituir el mismo valor de x para cada función y cuyo valor de la función sea mayor, será la función que quede por encima. Vamos a sustituir por ejemplo por x=0 en ambas funciones:
Vemos nuevamente que la función 4-x² da como resultado un valor mayor que x+2, por lo que queda demostrado que 4-x² es el límite superior.
Por tanto, una vez que sabemos los límites, ya podemos escribir al integral iterada doble:
Que queda:
Ahora integramos primero la integral que queda dentro, es decir, la que depende de dy, mediante la regla de Barrow:
Sustituimos el resultado de la integral por el límite superior y le restamos el resultado de sustituir el resultado de la integral por el límite inferior:
Operamos dentro del paréntesis:
Nos queda una integral que depende de la variable x. Integramos aplicando la regla de Barrow:
Restamos sustituyendo el límite superior menos el límite inferior:
Operamos y llegamos a la solución:
No te olvides que la solución debe estar en unidades cuadradas, ya que estamos calculando áreas.
Ejercicio resuelto 2
Dibujar la región cuya área viene dada por la integral:
Representar esa misma área cambiando el orden de integración a dy.dx u verificar que las dos integrales dan el mismo resultado.
Vemos que el orden de integración es dx.dy y que la región está definida por los límites:
Eso quiere decir que en este caso dy se representa por un rectángulo horizontal, que los límites exteriores de la integral doble, 0 y 2, son los límites entre los cuales se puede mover dy verticalmente y los límites internos y² y 4, son los límites entre los que se adapta la longitud del rectángulo dy.
En otras palabras, el área está acotada a la izquierda por la función y² y a la derecha por la recta x=4. Además está acotada inferiormente por el eje x (y=0) y superiormente por el valor 4 (y=4):
Vamos a calcular el valor de esta integral:
Integramos y aplicamos la regla de Barrow para la integral interior, integrada con respecto a x:
Ahora hacemos lo mismo para la integral que nos queda, integrada con respecto a y:
Ahora vamos a cambiar el orden de integración a dy.dx.
Para ello, en primer lugar, definimos la función en función de x, despejando la y:
Ahora, en la región anterior, colocamos el triángulo vertical dx:
Vemos que el triángulo se puede desplazar horizontalmente entre los valores de x 0 y 4:
Los cuales son los límites de integración externos para la variable x.
Además vemos que la altura del rectángulo dx se mueve entre el eje x (y=0) y la función (ahora definida en función de x):
Los cuales son los límites internos de integración para la variable «y», luego el área de la región viene dada por la integral:
Vamos a demostrar que el resultado es el mismo que con la integral anterior.
Integramos la integral interior y aplicamos la regla de Barrow:
Hacemos lo mismo con la integral que nos queda:
Y vemos que efectivamente el resultado es el mismo.
Cálculo de áreas con más de una integral iterada doble
En ocasiones no es posible calcular el área de una región con una única integral. En estos casos se puede dividir al región en subregiones, cuyas áreas sean calculables mediante integrales iteradas dobles.
El área total será la suma de las áreas.
Vamos a ver un ejemplo:
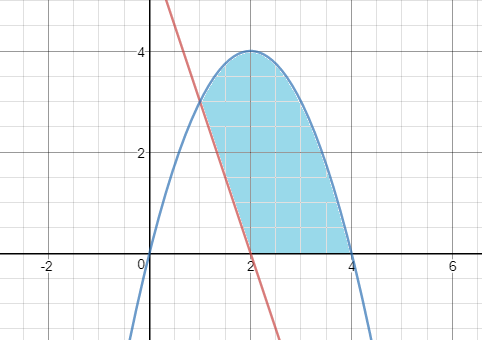
Calcular el área de la región R comprendida entra la parábola y=4x-x², el eje x y por encima de la recta y=-3x+6:
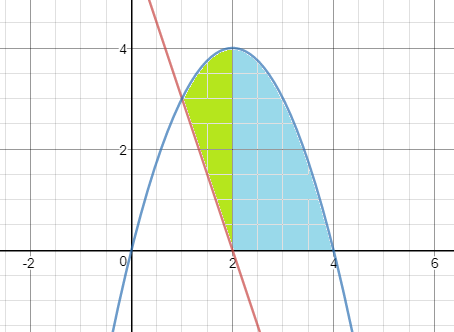
En primer lugar, dividimos el área de dos partes, en el punto donde la recta corta al eje x:
En ambas regiones conviene utilizar el rectángulo vertical dx y por tanto el orden de integración será dy.dx
La región de la izquierda queda definida entre los puntos 1 y 2 (los puntos corte de la recta con la parábola y el eje x respectivamente) que es por donde puede moverse horizontalmente el rectángulo:
y corresponden al los límites exteriores.
Los límites interiores para integrar con respecto a y, los determina la altura del rectángulo que está acotado inferiormente por la recta y superiormente por la parábola:
En la región de la derecha, el triángulo vertical dx, puede moverse entre los puntos 2 y 4 (punto de corte de la recta con el eje x y de la parábola con el eje x):
Y la altura del rectángulo la determinan inferiormente el eje x (y=o) y superiormente la parábola. Por los que los límites interiores para integrar con respecto a «y» son:
Por tanto, el área vendrá determinada por la suma de las dos integrales:
Que las resolvemos y queda:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: