A continuación vamos a ver la intersección de planos en el sistema diédrico, con ejercicios resueltos paso a paso. Te explicaré con todo detalle, los diferentes casos que se te pueden presentar y cómo resolverlos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
La intersección de dos planos
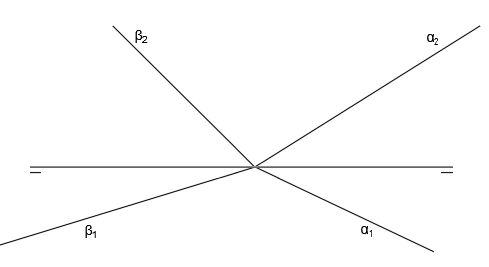
La intersección de dos planos da como resultado una línea recta, tal y como puedes observar en el siguiente esquema en tres dimensiones:
La intersección del plano α con el plano β da como resultado la recta i.
Si te das cuenta, la traza vertical de la recta V, coincide con la intersección de las trazas verticales de los planos α2 y β2. De la misma forma, la traza horizontal de la recta H, coincide con la intersección de las trazas horizontales de los planos α1 y β1. Esto nos da una pista para hallar la intersección de dos planos en diédrico, que será lo que veamos en el siguiente apartado.
Intersección de dos planos en el sistema diédrico. Ejercicios resuelto
¿Cómo realizar la intersección de dos planos en el sistema diédrico?
Como sabemos, la intersección de dos planos da como resultado una recta, por lo que tenemos que hallar dicha recta intersección.
Vamos a ver cómo hacerlo paso a paso, mediante un ejemplo.
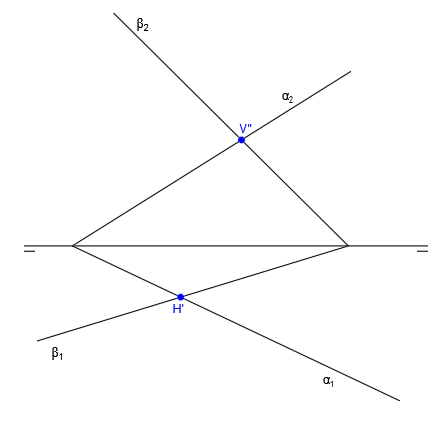
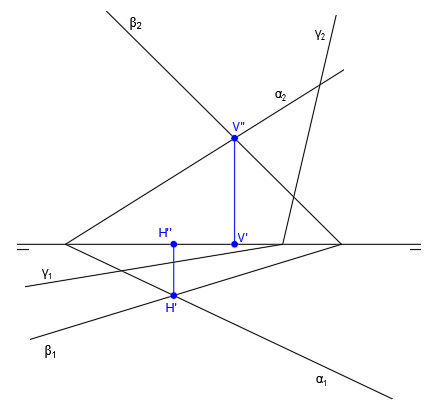
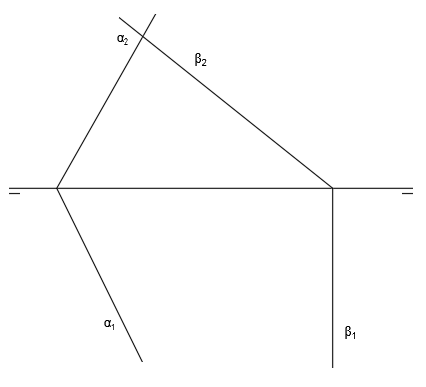
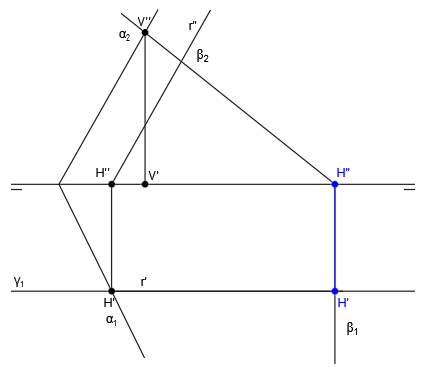
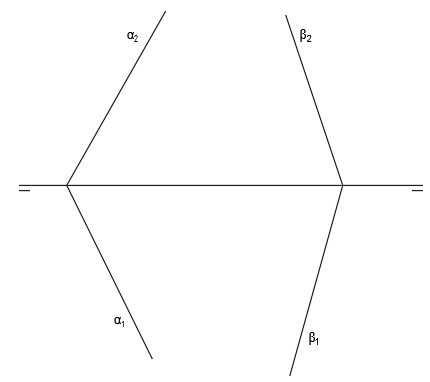
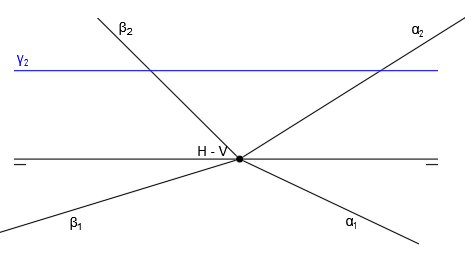
Tenemos los siguientes dos planos representados en el sistema diédrico mediante sus correspondientes trazas:
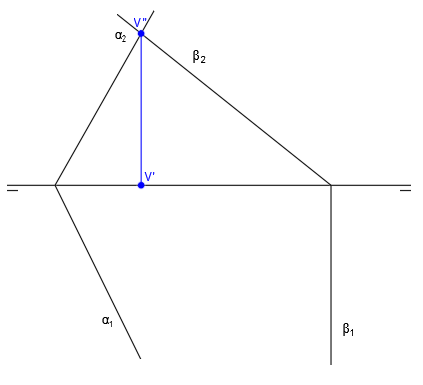
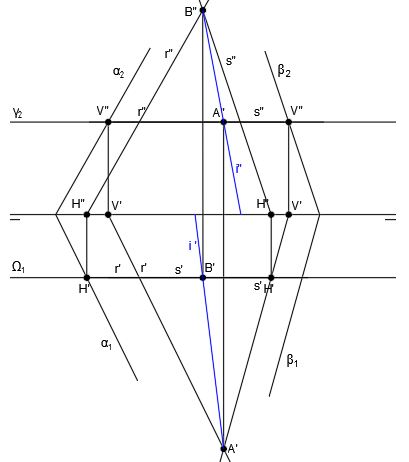
Tal y como hemos comentado antes, los puntos donde se unen las trazas de los planos coincidirán con las trazas de la recta intersección, por lo que el punto donde se unen α2 y β2 será la proyección vertical de la traza vertical de la recta intersección (V”) y el punto donde se unen α1 y β1 será la proyección horizontal de la traza horizontal de la recta intersección (H’):
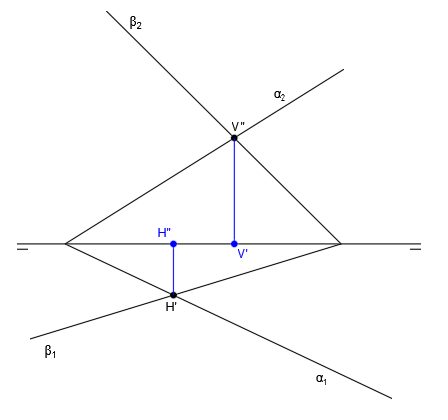
A partir del punto V”, trazamos una línea vertical hacia abajo. El punto de corte de esa línea vertical con la línea de tierra será la proyección horizontal de la traza vertical V’.
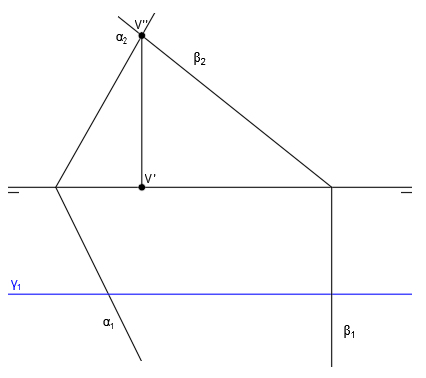
A partir del punto H’, trazamos una línea vertical hacia arriba. El punto de corte de esa línea vertical con la línea de tierra será la proyección vertical de la traza horizontal H”:
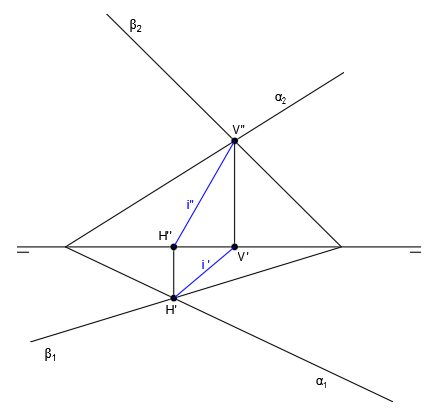
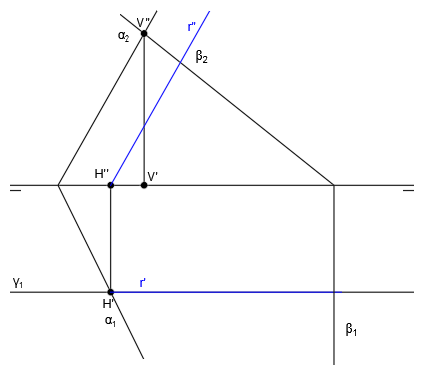
Ya tenemos las proyecciones de las trazas de la recta, por lo que para trazar la recta intersección i, sólo tenemos que unir dichas trazas.
Para trazar la proyección vertical de la recta i”, unimos H” con V” y para trazar la proyección horizontal de la recta i’, unimos H’ con V’:
Por lo tanto, hemos llegado al resultado final de la intersección de los planos α y β, que es la recta i.
El procedimiento que acabamos de seguir, es el procedimiento general para hallar la intersección de dos planos, aunque más abajo veremos ciertas particularidades. Te lo resumo a continuación:
- Hallar V” como resultado de la unión de α2 y β2 y H’ como resultado de la unión de α1 y β1.
- Hallar V’ y H”, trazado líneas verticales hasta que se corten con la línea de tierra.
- Unir H” con V” para trazar la proyección vertical de la recta i”.
- Unir H’ con V’ para trazar la proyección horizontal de la recta i’.
Cómo realizar la intersección de tres planos en el sistema diédrico
Si la intersección de dos planos da como resultado una recta, la intersección de tres planos da como resultado un punto, ya que si intersecamos los tres planos dos a dos obtenemos como resultado 3 rectas que se unen en un mismo punto.
Vamos a ver por qué la intersección de tres planos es un punto más despacio.
Imaginemos que tenemos tres planos α, β y γ.
- La intersección de los planos α y β da como resultado la recta r
- La intersección de los planos α y γ da como resultado la recta s
- Las rectas r y s se cortan en el punto P
- Si realizamos la intersección de los planos β y γ, daría como resultado la recta t, que también pasaría por el punto P
- Por tanto, las rectas r, s y t (rectas intersección de los planos dos a dos) se cortan en el punto P
Para hallar el punto P, resultado de la intersección de los tres planos, basta con con hallar dos rectas intersección, ya que estas dos rectas ya se cortarán en el punto P.
Vamos a realizar paso a paso la intersección de tres plano en el sistema diédrico, que consiste en hallar el punto de intersección P.
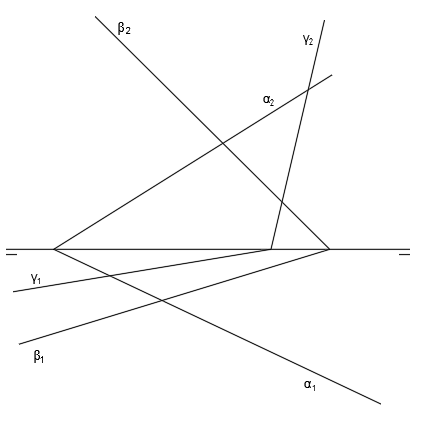
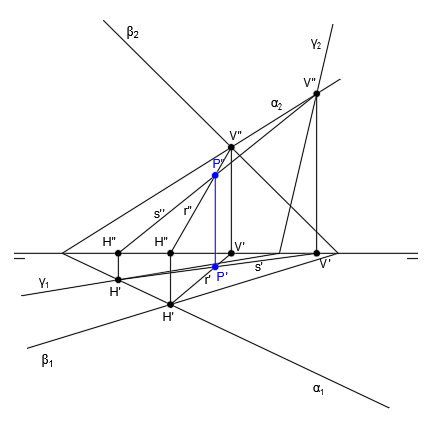
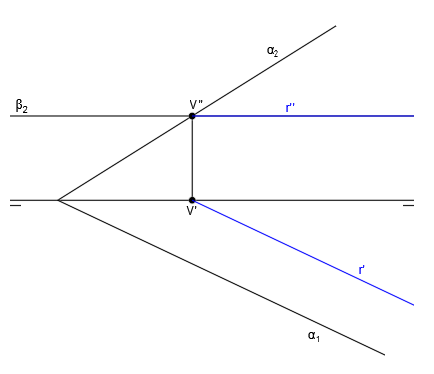
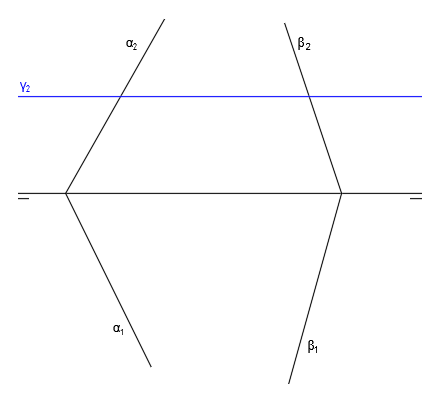
Tenemos los siguientes tres planos representados en diédrico:
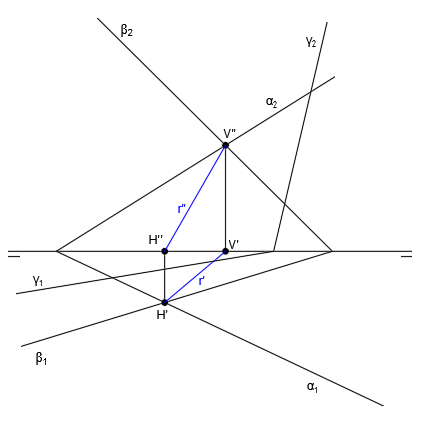
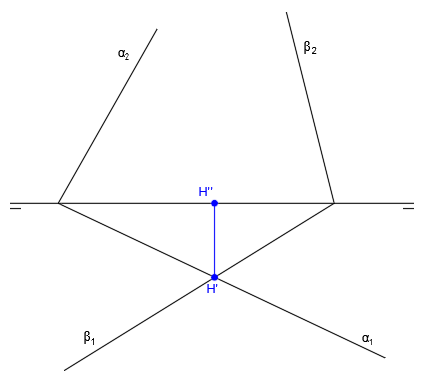
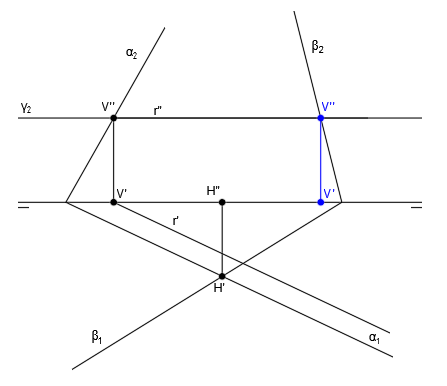
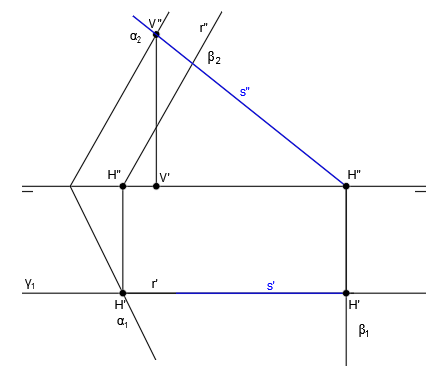
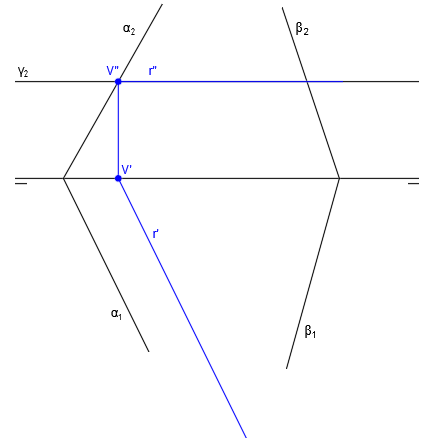
En primer lugar, vamos a hallar la recta intersección de los planos α y β. Para ello seguimos el procedimiento general y hallamos V” en el punto de corte de α2 y β2, H’ en el punto de corte de α1 y β1 y luego H” y V’, trazando líneas verticales hasta que corten con la línea de tierra:
Ahora unimos las trazas para dibujar las proyecciones de la recta r, que es la recta intersección de los planos α y β. Para trazar r” unimos H” y V” y para trazar r’ unimos H’ y V’:
Ya tenemos la recta r, que es la recta intersección de los planos α y β.
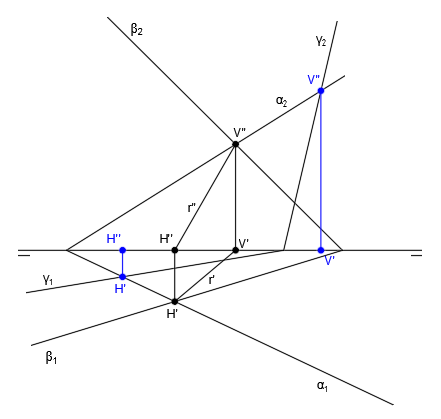
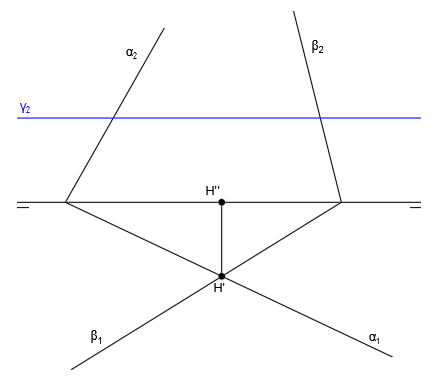
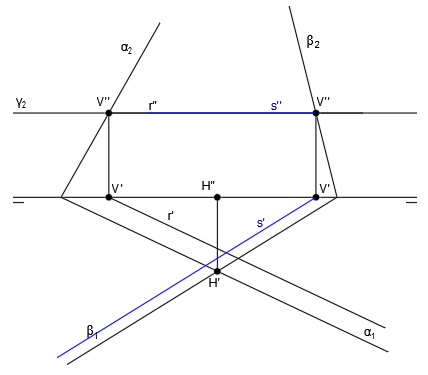
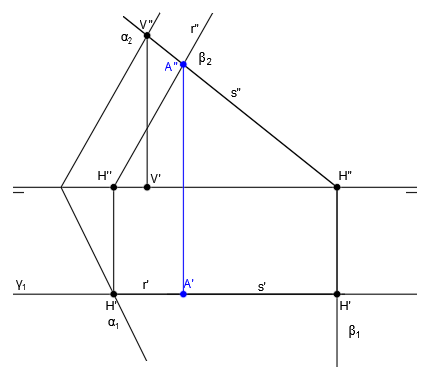
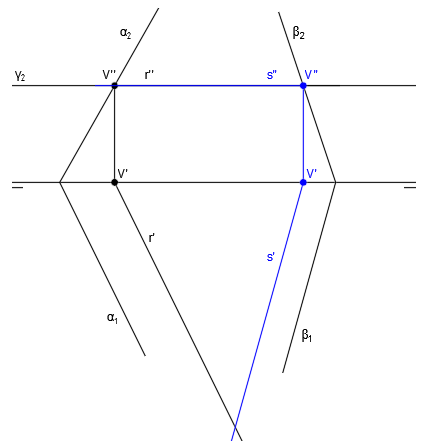
Ahora repetimos el proceso para hallar la intersección de los planos α y γ. Para ello hallamos las trazas V”, V’, H” y H’ siguiendo el procedimiento habitual:
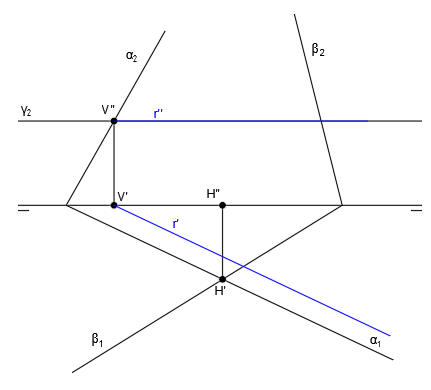
Unimos las trazas para dibujar las proyecciones de la recta s, recta intersección de los planos α y γ. Para trazar s” unimos H” y V” y para trazar s’ unimos H’ y V’:
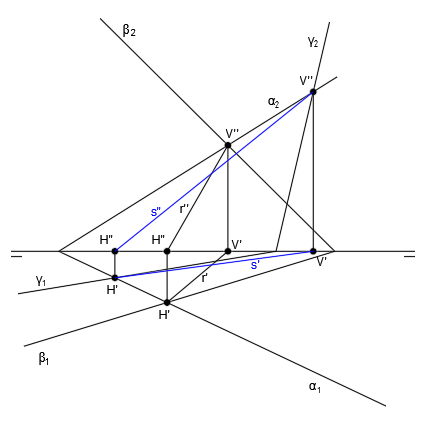
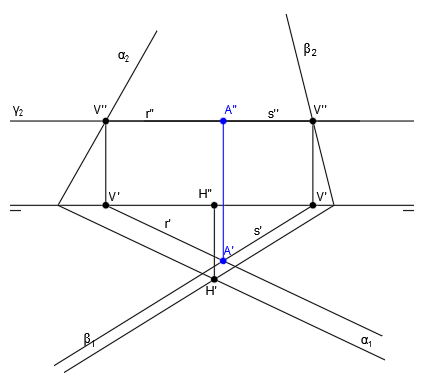
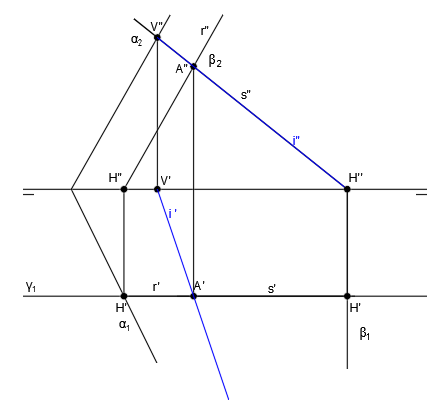
Las rectas r y s se cortan en el punto P. Las proyecciones r” y s” se cortan en P” y las proyecciones r’ y s’ se cortan en P’. P” y P’ se encuentran en la misma vertical, lo cual nos indica que se tratan de las proyecciones del punto P:
En este punto, ya habríamos terminado el ejercicio, ya que sabemos que tres planos se intersecan en un punto y basta hallar dos rectas intersección para encontrar ese punto de corte.
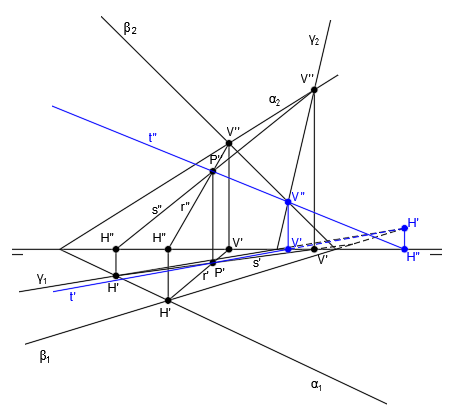
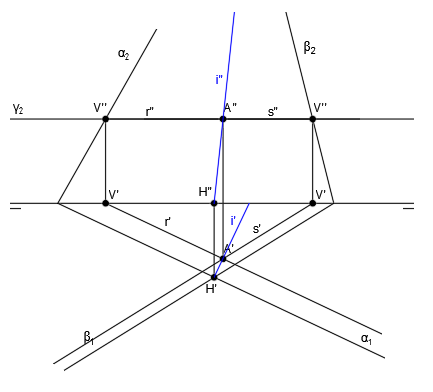
Como comprobación, si hallamos la recta t, intersección de los planos β y γ, observamos como también pasa por el punto P, ya que las rectas r, s y t se cortan en el mismo punto:
Intersección de un plano oblicuo con un plano horizontal
Vamos a ver ahora cómo realizar la intersección de un plano oblicuo con un plano horizontal.
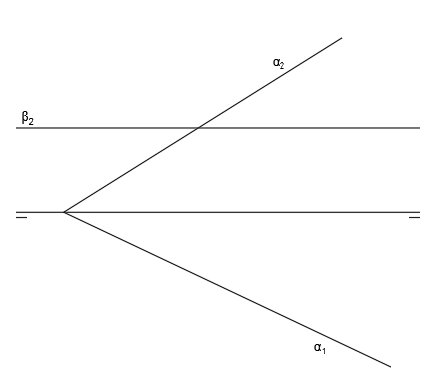
Por ejemplo, tenemos representados a continuación en diédrico el plano oblicuo α y el plano horizontal β:
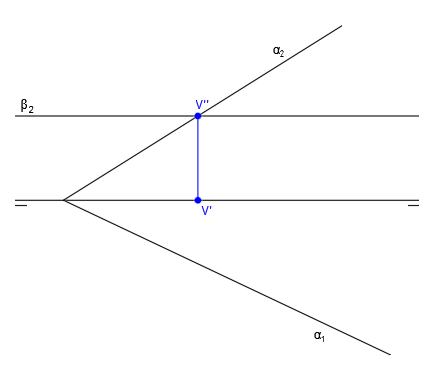
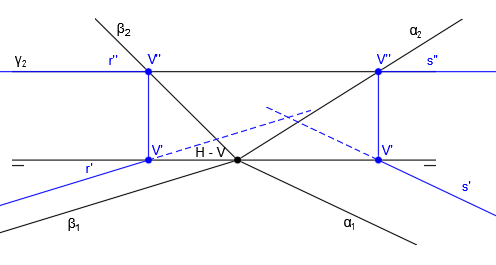
Siguiendo el procedimiento general, el punto donde se unen α2 y β2 será la proyección vertical de la traza vertical de la recta intersección (V”) y hallamos V’ trazando un vertical hasta que corte con la línea de tierra:
En este caso, no podemos hallar la traza horizontal de la recta ya que no tenemos traza horizontal del plano, así que la recta resultante de la intersección de un plano oblicuo con uno horizontal será una recta horizontal, cuya proyección vertical r”, paralela a la línea de tierra pasa por el punto V” y coincide con β2 y su proyección horizontal r’ es paralela a α1 y pasa por el punto V’:
La intersección de un plan oblicuo con uno horizontal la utilizaremos para resolver ejercicios más complejos de intersecciones entre planos, tal y como veremos más abajo.
Intersección de un plano oblicuo con un plano vertical
Siguiendo un razonamiento similar al del apartado anterior, llegamos a la conclusión de que la intersección de un plano oblicuo con uno vertical será una recta frontal:
Intersección de dos planos que no se cortan en diédrico
Vamos a ver cómo realizar la intersección de dos planos cuyas trazas no se cortan dentro del papel. Veremos paso a paso cada uno de los casos que se pueden presentar.
Intersección de dos planos cuyas trazas verticales no se cortan en el papel
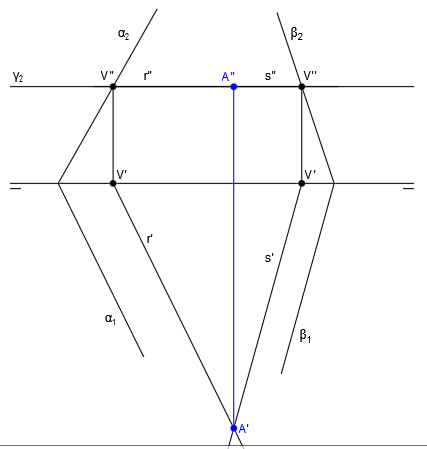
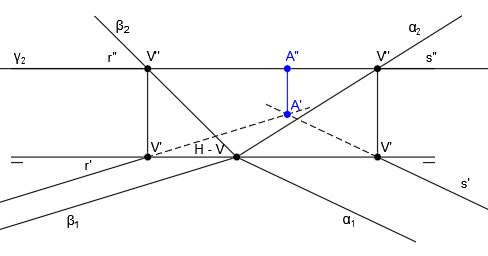
Tenemos el caso de la intersección de dos planos, cuyas trazas verticales no se cortan dentro del papel, como por ejemplo:
Hallamos como siempre las proyecciones de la traza horizontal de la futura recta intersección H’ y H”:
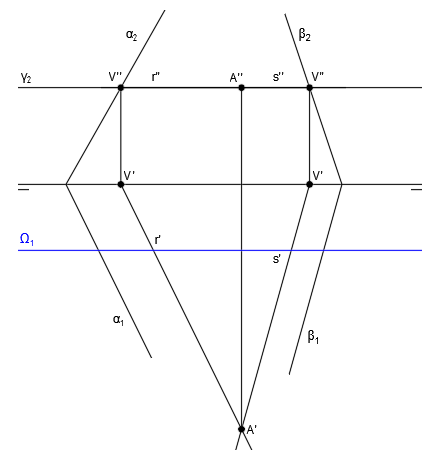
No podemos hacer lo mismo en el plano vertical, ya que las trazas no se cortan, por tanto, para poder seguir hallando la intersección de planos, utilizaremos un plano auxiliar γ, que se trata de un plano horizontal:
Ahora tenemos tres planos, por lo que encontrando la intersección del plano horizontal auxiliar con los otros dos planos, obtendremos el punto A, donde se intersecan los tres planos, punto por el que también pasará la recta intersección de los dos planos originales. La recta intersección que estamos buscando pasará por el punto A y la traza H, por lo que ya tendríamos dos puntos que unir para trazar dicha recta.
Vamos a verlo más despacio paso a paso.
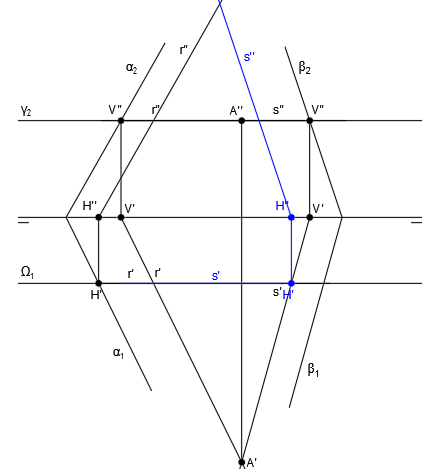
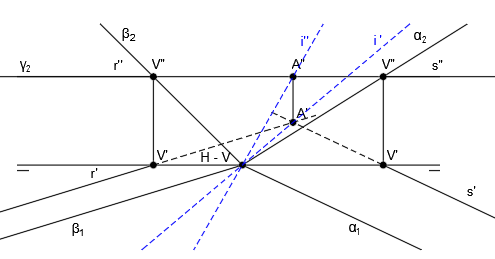
En primer lugar trazamos la recta intersección del plano α con el plano auxiliar horizontal γ. Obtenemos la traza V”, que es el punto de corte de α2 con γ2
Ahora trazamos la recta intersección de α y γ, que es una recta horizontal que pasa por V”, cuya proyección vertical es paralela a la línea de tierra y cuya proyección horizontal es paralela a α1, tal y como explicamos más arriba:
De la misma forma, trazamos la recta intersección del plano β con el plano auxiliar horizontal γ:
Las rectas r y s se corta en el punto A. El punto A’ es el punto de corte entre r’ y s’ y para hallar A”, trazamos una línea vertical hasta cortar a las proyecciones r” y s” (que coinciden):
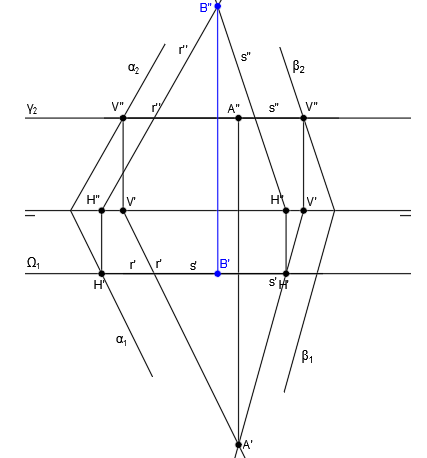
Ahora solo tenemos que unir los puntos A y H para encontrar la recta intersección que estamos buscando.
Unimos H” con A” para trazar i” y H’ con A’ para trazar i’:
Intersección de dos planos cuyas trazas horizontales no se cortan en el papel
Vamos a ver ahora cómo hallar la intersección de dos planos cuyas trazas horizontales no se cortan en el papel, como por ejemplo:
El procedimiento es muy similar al caso anterior, por lo que no me detendré en demasiados detalles.
En primer lugar obtenemos la traza V” y V’:
Dibujamos un plano horizontal auxiliar frontal en el plano horizontal:
Hallamos la intersección de los planos α y γ, cuyo resultado es la recta vertical r:
Seguimos con la intersección de los planos β y γ, cuyo resultado es la recta frontal s. En este caso, como la traza horizontal del plano β es perpendicular a la línea de tierra, las proyecciones de la recta s coincide con las trazas del plano β:
El punto de corte de r” y s” es A” y trazamos una vertical hasta r’ y s’ para obtener A’:
Finalmente, unimos V” y A” para trazar i” y A’ y V’ para trazar i’:
Intersección de dos planos cuyas trazas no se cortan en el papel
Ahora vamos a ver cómo realizar la intersección de dos planos cuyas trazas no se cortan en el papel, ni las horizontales ni las verticales, como por ejemplo:
Este caso se resuelve utilizando un plano vertical auxiliar en el plano vertical y otro plano horizontal auxiliar en el plano horizontal.
Vamos a verlo paso a paso.
Trazamos un plano auxiliar horizontal en el plano vertical:
Hallamos la recta r, intersección del plano α con el plano auxiliar:
Hallamos la recta s, intersección del plano β con el plano auxiliar:
Obtenemos el punto de corte A, entre r y s:
Ahora trazamos un plano auxiliar vertical en el plano horizontal:
Hallamos la recta intersección de el plano auxiliar y el plano α:
Hallamos la recta intersección de el plano auxiliar y el plano β:
El punto de corte entre las dos últimas rectas es el punto B:
Para trazar la recta intersección de los planos originales α y β, unimos los puntos A y B. Unimos A” y B” para trazar i” y A’ y B’ para trazar i’:
Cómo realizar la intersección de dos plano unidos por el vértice en diédrico
¿Cómo se realiza la intersección de dos planos cuyas trazas están unidas en el mismo vértice?
Vamos a ver un ejemplo. Tenemos los siguientes planos en diédrico unidos por el vértice:
El vértice de ambos planos, coincide con la traza horizontal y vertical, por lo que por este punto pasará la recta intersección de ambos planos:
Para encontrar el segundo punto de nuestra recta intersección, utilizaremos un plano auxiliar horizontal, ya que como sabemos, hallaremos un punto donde se cortan las rectas intersección del plano auxiliar con los dos planos y por ese punto, también pasará la recta intersección de los planos α y β:
Trazamos las dos rectas de intersección del plano auxiliar con los planos α y β:
El punto de corte de ambas rectas da como resultado el punto A:
La recta intersección de los planos α y β, pasa por el punto A y la traza H-V. Unimos A” y la traza H-V para dibujar i” y A’ y la traza H-V para dibujar i’:
En este caso, las proyecciones de la recta i no pasan por el primer cuadrante, por lo que se dibujan con línea contínua.
Intersección de dos planos paralelos a la línea de tierra
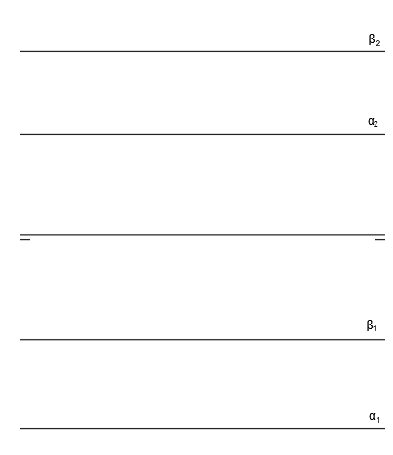
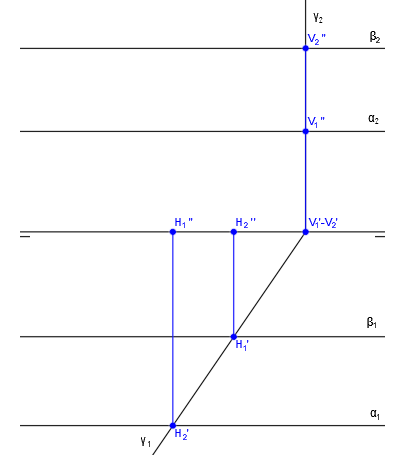
Éste es un caso particular de intersección de planos en el sistema diédrico, ya que sus trazas no se cortan al ser paralelas a la línea de tierra:
Intuitivamente, sabemos que su intersección se tratará de una recta paralela a la línea de tierra, por lo que sólo necesitamos un punto de ella para poder trazarla y eso lo realizaremos con un sólo plano auxiliar, el cual será un plano proyectante del plano vertical u horizontal.
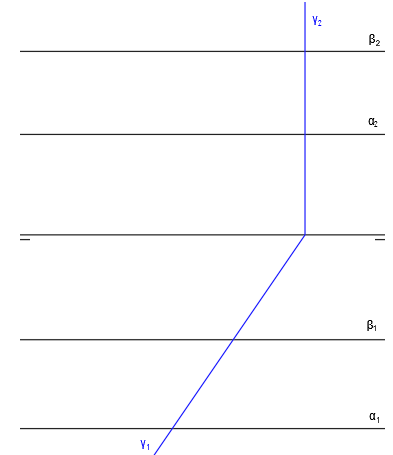
En nuestro caso utilizaremos un plano proyectante del plano horizontal:
La intersección de este plano proyectante auxiliar con los dos planos dados, dan lugar a dos rectas de intersección, que se cortarán en un punto. Por este punto va a pasar la recta intersección, paralela a la línea de tierra, que estamos buscando.
La traza vertical del plano auxiliar, γ2, corta a las trazas verticales de los planos dados, α2 y β2, en los puntos V1” y V2”, los cuales corresponden a las proyecciones de las trazas verticales de las rectas intersección.
La traza horizontal del plano auxiliar, γ1, corta a las trazas horizontales de los planos dados, α1 y β1, en los puntos H1′ y H2′, los cuales corresponden a las proyecciones de las trazas horizontales de las rectas intersección.
Obtenemos las trazas restantes de las rectas intersección, H1”, H2”, V1′ y V2′, trazando líneas auxiliares hasta cortar a la línea de tierra. V1′ y V2′ coinciden en el mismo punto al estar V1” y V2” en la misma vertical:
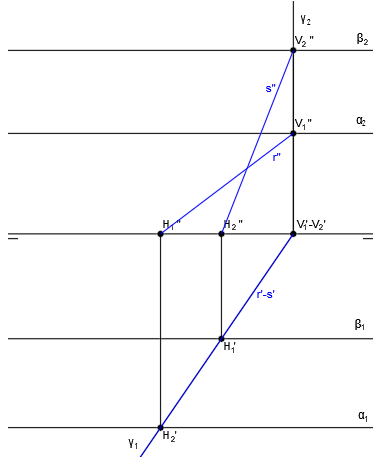
Ahora trazamos las proyecciones de las rectas r y s. La recta r es la recta intersección de los planos α y γ y la recta s es la recta intersección de los planos β y γ. Para ello unimos H1” con V1” para trazar r”, H1′ con V1′ para trazar r’, H2” con V2” para trazar s”, H2′ con V2′ para trazar s’:
Las proyecciones de las rectas r’ y s’ coinciden entre ellas y además coinciden con la traza horizontal del plano γ.
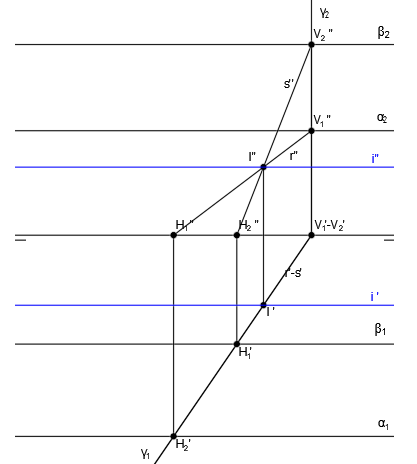
El punto de corte de r” y s” será el punto I”. Para hallar I’ trazamos una línea vertical hasta que corte a las rectas r’ y s0:
Ya tenemos el punto por donde pasará la recta intersección que estamos buscando, que será paralela a la línea de tierra. Por tanto, dibujamos las proyecciones de la recta i, i’ e i”, paralelas a la línea de tierra y que pasan por el punto I:
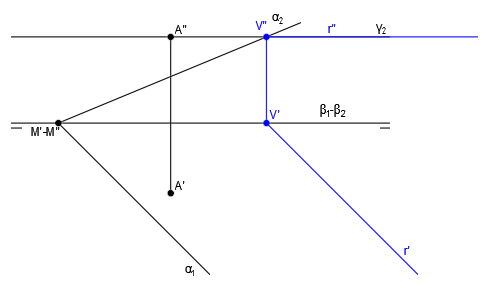
Intersección de un plano LT-punto con un plano oblicuo
Éste es otro caso particular de intersección de planos, al no poder identificar claramente los puntos de corte entre las trazas de los planos.
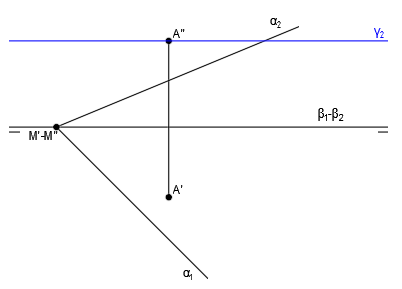
Tenemos un plano LT-punto y un plano oblicuo:
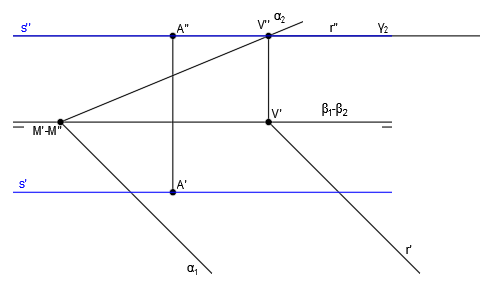
En este caso conocemos un punto de la intersección, que se encuentra en el vértice del plano α (M’-M”), ya que dicho punto es un punto del plano α que está en la línea de tierra y la línea de tierra está totalmente incluida en el plano LT-punto:
Para hallar el punto de la recta intersección que nos falta, utilizaremos un plano auxiliar horizontal, que además pase por el punto A:
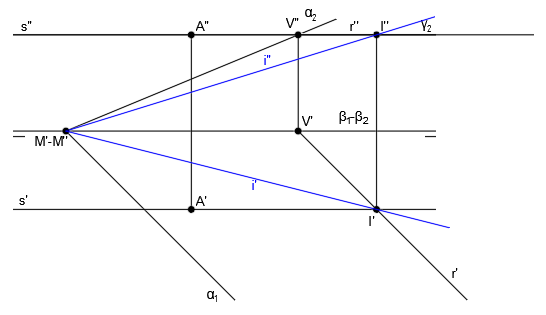
La intersección del plano auxiliar γ con el plano oblicuo α da lugar a la recta horizontal r:
La intersección del plano auxiliar γ con el plano LT-punto β es la recta s, paralela a la línea de tierra, que pasa por el punto A:
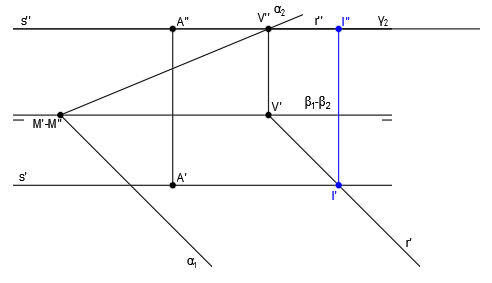
La intersección de r con s da lugar al punto I. Obtenemos I’ en el punto de corte de r’ y s’ y a partir de I’, obtenemos I”, trazando una línea vertical hasta cortar con r” y s”:
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE