In un esercizio vi viene chiesto di utilizzare la regola Ruffini. Sei pronto a farlo ma ti rendi conto che non sai nemmeno come iniziare. Hai visto il tuo insegnante farlo più volte in classe, ma ora non sai come usare il metodo di Ruffini.
Ma ora, qual è la regola o metodo Ruffini e a cosa serve? La regola Ruffini è un metodo che permette:
- Risolvere equazioni di terzo grado o superiori (quarto grado, quinto grado ….)
- Dividere un polinomio tra un binomio che è della forma x-a
- Fattore polinomiali di terzo grado o superiore (quarto grado, quinto grado ….)
- Calcolare le radici dei polinomi di un grado superiore o uguale a 3
Regola Ruffini per risolvere equazioni e factoring
Come discusso nell’introduzione, la regola Ruffini viene utilizzata per risolvere equazioni di terzo grado o superiori.
Per risolvere equazioni di primo grado si usa un metodo, per le equazioni di secondo grado si usa un altro metodo e per risolvere equazioni di terzo grado o superiori, o in altre parole, per equazioni superiori a due gradi, si usa il metodo Ruffini.
Con la regola Ruffini si ottengono solo soluzioni complete. Se l’equazione ha soluzioni complesse o reali, questo metodo non è valido.
Vedremo che per ottenere le soluzioni dell’equazione, è necessario tenere conto in precedenza, quindi con lo stesso esempio spiegheremo entrambi i concetti.
Risolviamo un esempio spiegandolo passo dopo passo.
Abbiamo la seguente equazione:
1 – Identifichiamo i coefficienti di ogni termine, che sono i numeri che precedono l’ignoto. Per l’equazione di cui sopra, li rappresento in verde per identificarli:
2 – Disegniamo due linee perpendicolari in questo modo:
3 – Poniamo i coefficienti ordinati in base al loro grado di maggiore o minore:
Nella regola di Ruffini, il grado diminuisce uno per uno e ogni grado ha il suo posto. Per esempio, se non avessimo un termine che ha x², al posto del grado 2, verrebbe posto uno 0.
I numeri che abbiamo scritto finora nel metodo Ruffini equivalgono a scrivere l’equazione, cioè:
4 – Ora scriviamo un numero a sinistra della linea verticale. Spiegheremo in seguito quale numero collocare qui e perché. Per ora, iniziamo con 1.
Questo numero corrisponde al numero (a) del binomio x – a:

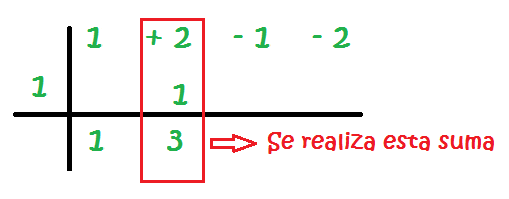
5 – Iniziamo ad eseguire il metodo. La prima buca della seconda fila è sempre lasciata libera:
6 – La somma della prima colonna è fatta e il risultato è messo giù:
7 – Il numero a sinistra è moltiplicato per il risultato della somma della prima colonna. Il risultato è posto nella cavità della seconda colonna:
8 – Viene aggiunta la seconda colonna:
9 – Il numero a sinistra è moltiplicato per il risultato della somma della seconda colonna. Il risultato è posto nella cavità della terza colonna:
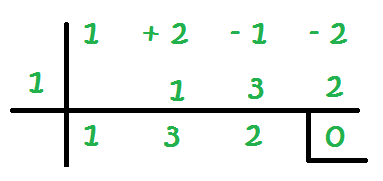
10 – Così via fino al completamento di tutte le colonne:
L’obiettivo è che nell’ultima colonna abbiamo uno 0. Questa è la spiegazione di quale numero posizionare a sinistra della linea:
Se non abbiamo uno zero, dovremmo provare un altro numero a sinistra della linea verticale e riavviare il processo
[hr]
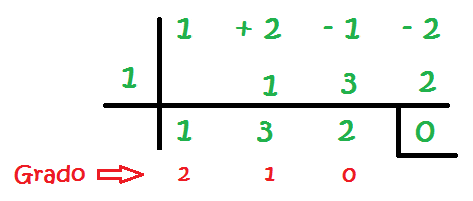
Una volta che abbiamo uno zero alla fine, vediamo cosa significa quello che abbiamo finora:
Quello che abbiamo lasciato nell’ultima riga è un’altra equazione, ma ora, il numero che è a sinistra dello 0, ha il grado 0 e questa sta aumentando di 1 in 1 verso sinistra. In questo caso, ci rimane l’equivalente di avere questa equazione:
E come abbiamo visto prima, l’1 a sinistra della linea verticale significava:
Il che significa che quello che abbiamo finora è il prodotto di queste due equazioni, che è uguale all’equazione originale:
[hr]
11 – Con la fila che abbiamo lasciato, ricominciamo da capo. Iniziamo con la prova 1:
12 – Come prima, ci moltiplichiamo con il risultato dell’aggiunta in ogni colonna:
Alla fine abbiamo un 6, e quello che vogliamo è avere uno zero. Pertanto, dobbiamo continuare a testare, con -1, con 2, con -2….. fino a trovare il numero che ci fa avere uno zero nell’ultima colonna.
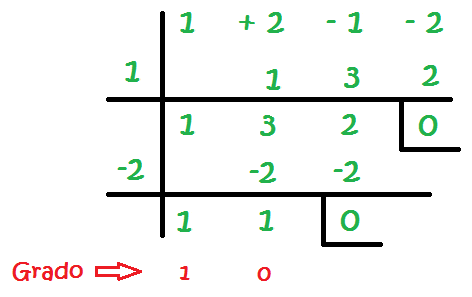
Il numero che ci fa avere uno 0 alla fine è -2:
Cosa facciamo ora? Come sappiamo di aver finito?
Il voto più alto nell’ultima fila è 1, quindi abbiamo finito:
Il risultato del calcolo dell’equazione con il metodo Ruffini è il prodotto dell’ultima riga e dei numeri che si trovano a sinistra della linea verticale, ma espressi sotto forma di equazione:
Pertanto, la nostra equazione sarà:
Finora abbiamo preso in considerazione l’equazione. Ora risolviamo il problema:
1 – Siamo uguali a 0, come era all’inizio
2 – Ricordate che quando una moltiplicazione di due o più fattori porta a 0, significa che uno dei fattori è 0, poiché ogni valore moltiplicato per 0 è 0. Pertanto, ogni fattore potrebbe essere 0.
Ci rimangono tre equazioni di primo grado da chiarire, da cui si ottengono le tre soluzioni (trattandosi di un’equazione di terzo grado):
Soluzioni -1, -2 y 1
La regola Ruffini per dividere i Binomiali del modulo x-a
In questo caso, la regola Ruffini serve a fare una divisione dei polinomi, dove il divisore è un binomio della forma (x-a).
Per esempio, ci viene chiesto di fare la divisione successiva:
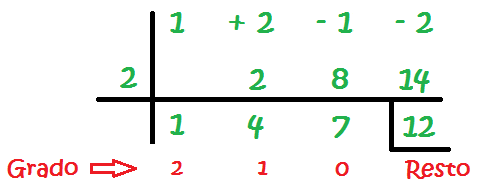
Poiché il divisore è x-2, cioè della forma x-a, usiamo la regola Ruffini. Dovremmo applicare la regola solo una volta.
Questa volta, il numero che dobbiamo posizionare a sinistra della linea verticale è 2 (la a di x-a) e non dobbiamo preoccuparci se abbiamo uno zero nella colonna finale o meno. Il risultato che ci darà sarà il resto della divisione:
Il quoziente di divisione sarà il polinomio formato dai coefficienti dell’ultima riga:
E il resto sarà l’ultimo elemento dell’ultima riga: