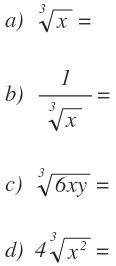En la lección anterior te estuve explicando cómo obtener el resultado de una raíz, especialmente de raíces cuadradas y cúbicas y te enseñé cómo podía influir el signo menos en el resultado.
En esta lección te voy a explicar cómo pasar de raíz a potencia y viceversa, con la forma exponencial de las raíces.
Hay veces en las que no es posible obtener el resultado de una potencia directamente al tener como exponente una fracción. Veremos a continuación cómo calcular esas potencias.
Por otro lado, pasar una raíz a su forma de potencia puede serte muy útil en un momento determinado si lo tuyo es trabajar con potencias.
Forma exponencial de las raíces
Signos menos en las potencias con exponente fraccionario
Potencias de exponente fraccionario con bases formadas por varios factores o términos
Ahora practica tú. Ejercicios propuestos
1) Calcula, si es posible, el valor de las siguientes expresiones:
2) Escribe como radical las siguientes potencias:
3) Escribe como potencia los siguientes radicales:
Saber pasar de raíz a potencia y de potencia a raíz, además de ayudarte a encontrar la solución de determinados ejercicios, te ayudará a entender las propiedades de la raíces, siempre y cuando domines las potencias, ya que las propiedades de las raíces son muy similares a las de las potencias.
En la siguiente lección voy explicarte cada una de las propiedades de las raíces y cómo hay que aplicarlas. Practicarás con ejercicios para que lo entiendas mejor.
Las propiedades de las raíces te van a ayudar mucho a resolver tus ejercicios, de hecho es una base fundamental.
¡Te espero en la siguiente lección!