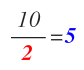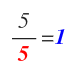En la lección anterior te estuve explicando explicando las reglas de divisibilidad. En esta lección te voy a enseñar a aplicarlas, mientras aprendes cómo descomponer un número en factores primos o también llamada descomposición factorial o factorización.
Los números se descomponen en factores primos porque se necesita trabajar con esos factores, como por ejemplo para calcular el mínimo común múltiplo o el máximo común divisor. Es una herramienta.
En esta lección vamos a centrarnos en que aprendas bien cómo descomponer un número en factores primos.
Qué es la descomposición factorial
En el siguiente video te cuento qué es la descomposición factorial
Aquí tienes el contenido del vídeo:
Descomponer un número en factores primos, como su propio nombre indica, es expresar ese número como un producto de factores y además, esos factores deben ser números primos.
Los números primos son aquellos que sólo son divisibles entre ellos mismos y entre 1. Con que te aprendas los números primos entre 1 y 30 es más que suficiente. Yo personalmente no me sé ninguno más:
2 – 3 – 5 – 7 – 11 – 13 – 17 – 19 – 23 – 29
Por tanto, podemos expresar un número como un producto de factores, como por ejemplo, 12 que es 4 por 3:
12 = 4 x 3
El 12 lo hemos expresado como el producto de dos factores 4 y 3. Pero esto no es una descomposición en factores primos porque el 4 no es un número primo.
Pero si lo expresamos de ésta otra forma:
12 = 2 x 2 x 3
Esto sí que es una descomposición en factores primos. El 2 y el 3, que son los factores en los que expresamos ahora el 12, son números primos.
Y ahora te preguntarás: ¿cómo se descompone cualquier número en factores primos? Es lo que vamos a ver en el siguiente apartado.
Cómo descomponer un número en factores primos
Vamos a ver cómo se realiza la descomposición factorial paso a paso:
Ideas principales del vídeo:
Para descomponer un número en factores primos necesitamos dominar las reglas de divisibilidad, que ya las estudiamos en la lección anterior y no deberías tener problemas con ellas. Si tienes alguna duda, por favor, pregúntamela, porque si no en esta lección te perderás.
Explicaré el procedimiento al mismo tiempo que realizamos un ejemplo:
Vamos a descomponer el número 6:
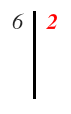
1 – En primer lugar, escribimos el número a factorizar y se traza una línea vertical a su derecha.
A la derecha de esta línea irán apareciendo los factores primos del número, en este caso, los factores primos del 6.
2 – Hay que buscar si el 6 es divisible entre algún número primo. Aquí es cuando entran en juego las reglas de divisibilidad.
Se empieza siempre comprobando si el número es divisible entre 2 y después se sigue en orden ascendente con el resto de números primos: con el 3, con el 5…
- ¿Es divisible entre 2? Lo comprobamos con la regla de divisibilidad del 2
- Si no es divisible entre 2, ¿es divisible entre 3? Lo comprobamos con la regla de divisibilidad del 3
- Si no es divisible entre 3, ¿es divisible entre 5? Lo comprobamos con la regla de divisibilidad del 5
- Y así sucesivamente…
Como he comentado antes, se empieza siempre con el 2 y para ello utilizamos la regla de divisibilidad del 2.
Nos preguntamos, ¿6 es divisible entre 2?
La respuesta es: Sí, porque es un número par.
Como es divisible entre 2, lo escribimos al la misma altura que el 6, a la derecha de la línea:
Ahora dividimos 6 entre 2:
Y el resultado, que es 3, lo colocamos a la izquierda de la línea, debajo del 6:
Ya tenemos el primer factor.
3 – Ahora volvemos a repetir el paso anterior pero en este caso con el 3, que fue el resultado de hacer la división anteriormente.
Empezamos buscando si es divisible entre 2:
¿3 es divisible entre 2? No porque no acaba en par
Como no es divisible entre 2, ahora seguimos con el 3:
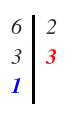
¿3 es divisible entre 3? Sí. Además 3 es un número primo por lo que directamente se coloca el 3 a la derecha de la línea:
Y hacemos la división del último número que tenemos a la izquierda, en este caso el 3, con el último factor que tenemos a la derecha, en este caso, otro 3:
Y el resultado lo colocamos debajo del último número a la izquierda de la línea, es decir, debajo del 3:
Y ya tenemos el 6 descompuesto en factores primos.
Cuando el último número que tengamos a la derecha sea un número primo y por tanto, el resultado de la división sea 1, quiere decir que hemos terminado de descomponer.
4 – Los números que quedan a la derecha de la línea son los factores primos. Por tanto, la descomposición factorial del 6 es:
6 = 2 x 3
Vamos a repetir este procedimiento con otro ejemplo, descomponiendo el número 40:
Trazamos la línea y lo colocamos a su izquierda:

Hacemos la división y el resultado lo colocamos debajo:
Ahora tenemos el 20 y volvemos a empezar.
¿20 es divisible entre 2? Sí porque acaba en 0. Volvemos a escribir el 2 a la derecha de la línea, dividimos 20 entre 2, y colocamos debajo el resultado:
Tenemos el 10.
Volvemos a empezar otra vez ¿10 es divisible entre 2? Sí, porque acaba en 0. Dividimos y a colocamos el resultado a la izquierda:
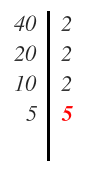
Nos queda el 5, que es un número primo, por lo escribimos en la parte derecha, dividimos y ya hemos terminado:
Los factores son los que están a la derecha y el 40 expresado como producto de sus factores primos es:
Si no te das cuenta de que el 5 es un número primo al principio, te darías cuenta después, siguiendo el proceso habitual:
- ¿5 es divisible entre 2? No porque acaba en 5
- ¿5 es divisible entre 3? No porque la suma de sus cifras no es múltiplo de 3
- ¿5 es divisible entre 5? Sí, porque acaba en 5. De hecho sólo se puede dividir entre 5 y entre 1 (5 es primo)
Date cuenta que cada vez que repetimos el proceso, siempre empezamos con el 2 y lo hacemos hasta que no se pueda más. Se haría lo mismo después con el 3
Ahora practica tú. Ejercicios propuestos
Ahora, te dejo que practiques con estos ejercicios. Realizalos en papel y envíame una imagen con tu solución por WhatsApp al 644 06 45 86 o por email a ayuda@ekuatio.com.
Una vez me los envíes, te enviaré la solución y te comentaré tus errores para que los tengas en cuenta para futuras lecciones
Y por su puesto, puedes preguntarme cualquier duda que no entiendas
Ejercicio 1
Descomponer en factores primos el número 24
Ejercicio 2
Descomponer en factores primos el número 108
Ejercicio 3
Descomponer en factores primos el número 90
Ejercicio 4
Descomponer en factores primos el número 150
Esta lección te ha servido para sentar las bases de cómo funciona la descomposición de un número en factores primos, con números en los que la descomposición factorial siempre sale bien, pero eso no va a ser siempre así. Hay veces que no es tan fácil encontrar los divisores del número a descomponer y eso es lo que te explicaré en la siguiente lección.
¡Hasta la siguiente lección! ¡Espero tus ejercicios!