A continuación vamos a estudiar las propiedades de las potencias, lo cual es fundamental para que aprendas a operar con potencias.
Estudiaremos paso a paso, con todo detalle, todas las propiedades de las potencias, con ejemplos resueltos para que las comprendas mejor y empieces a saber cómo funcionan.
¿Para que sirven las propiedades de las potencias? Pues nos permiten operar con las potencias y poder así simplificar expresiones mucho más complejas.
Lo interesante de las propiedades de las potencias no es sólo saberlas, sino saber aplicarlas.
Si has llegado hasta aquí es porque quieres aprender a resolver algún ejercicio. ¿Has pensado en apuntarte a clases de matemáticas online?. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Por cierto, si quieres aprender a trabajar con potencias, en el Curso de Potencias se explica todo paso a paso, para que operar con potencias te resulte muy sencillo. Te recomiendo echarle un vistazo.
Vamos a empezar definiendo qué es una potencia.
Qué es una potencia
¿Qué es una potencia?
Una potencia es un producto de factores que se repiten un número determinado de veces. El factor que se repite es la base y el número de veces que se repite es el exponente.
En este ejemplo, el 3 se multiplica 4 veces, por lo que se lee que el 3 está elevado a 4
En general se puede representar como:
Donde a es la base y n es el exponente.
Potencias con base negativa
Un caso particular de las potencias es cuando la base es negativa. En este caso, el resultado dependerá de si el exponente es par o impar. En general, una potencia con base negativa con exponente par, su resultado es positivo:
Una potencia con base negativa y exponente impar, el resultado es un número negativo:
Hay que tener mucho cuidado si el signo – no está dentro del paréntesis, ya que en ese caso, no está elevado con la potencia, sino que va a parte:
Es decir, el signo – es totalmente independiente de la potencia. Tenemos un signo menos seguido de un dos al cuadrado.
Seguimos con las propiedades de las potencias.
Propiedades de las Potencias
Aquí tienes un vídeo con las propiedades de las potencias y ejemplos de su aplicación:
Y aquí tienes las propiedades de las potencias en formato texto:
Potencias con exponente uno
Cualquier valor elevado a 1, da como resultado el mismo valor:
Esta propiedad es muy útil sobre todo cuando nos aparece un número o variable que no tiene exponente. En ese caso, sabemos que está elevada a 1 gracias a esta propiedad.
Ejemplo:
Potencias con exponente cero
Cualquier valor elevado a 0, tiene como resultado 1
Mucho cuidado con esta propiedad porque es muy común confundirse y pensar que cuando un número o variable está elevada a 0 es 0. Eso es un grave error.
Ejemplo:
No tiene por qué ser solo un número o una variable. Cualquier operación que esté elevada a 0, el resultado también es 1. Da igual lo que sea.
Multiplicación de potencias con la misma base
Multiplicación de potencias con la misma base: Se mantiene la base y se suman los exponentes:
Ejemplo:
¿Qué pasa si tienen distinta base? Si tienen distinta base no se puede utilizar esta propiedad:
En el Curso de Potencias te enseño qué hay que hacer si tenemos multiplicación de potencias con distinta base.
División de potencias con la misma base
División de potencias con la misma base: Se mantiene la base y se restan los exponentes:

Al igual que ocurre con la propiedad anterior, esta propiedad no se aplica si las potencias tienen distinta base.
Multiplicación elevada a una potencia
Cuando tenemos una multiplicación elevada a un exponente, el resultado es igual a cada factor elevado a ese mismo exponente:
Esta propiedad se aplica con variables para eliminar los paréntesis:
También puede utilizarse con números, pero en sentido inverso, es decir, cuando tenemos dos números con el mismo exponente:
¡Mucho cuidado! Esta propiedad sólo funciona con la multiplicación. No funciona con sumas y restas.
Para resolver las sumas y restas al cuadrado utilizamos los productos notables.
Cociente elevado a una potencia
Cociente elevado a una potencia: Es igual al numerador y al denominador elevados a la misma potencia:
Propiedad muy útil para eliminar paréntesis en expresiones más complejas:
O si trabajamos con números, nos sirve para calcular el resultado:
Si podemos operar dentro del paréntesis, también podemos resolver la potencia sin aplicar esta propiedad, solamente resolviendo el paréntesis y después elevarlo al exponente:
Potencia de otra potencia
Potencia elevada a otra potencia: Se mantiene la base y se multiplican los exponentes:
Puedes encontrarte la potencia de potencia sin paréntesis, pero eso no es lo correcto. Debe llevar paréntesis para indicar que se está elevando toda la potencia a otra potencia.
Ejemplo:
Esta propiedad se combina con las dos propiedades anteriores.
Cuando tenemos una multiplicación o división de potencias, elevadas a otra potencia, el exponente de fuera multiplica a cada uno de los exponentes de dentro del paréntesis.
Con la multiplicación:
Por ejemplo:
Y con la división:
Por ejemplo:
Potencias con exponente negativo
Potencias de exponente negativo: Un valor elevado a una potencia negativa, es equivalente a 1 dividido entre el valor elevado a la misma potencia positiva:
Ejemplo:
Como caso particular de esta propiedad esta la inversa de un número, que es cualquier valor elevado a -1:
Fracción elevado a exponente negativo: En este caso se le da la vuelta a la fracción y el exponente se pone positivo:
Potencia de exponente racional
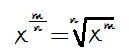
El denominador del exponente se convierte en el índice de la raíz
Potencia de exponente racional y negativo

Si quieres aprender todo sobre las potencias, como saber aplicar sus propiedades y operar con operaciones con potencias, te recomiendo el Curso de Potencias, con ejercicios resueltos paso a paso y propuestos para practicar.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:







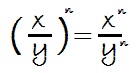
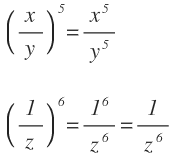

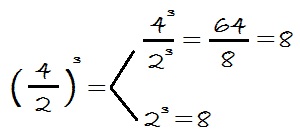




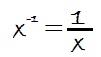

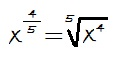
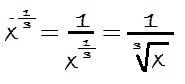
Hola docente, puede orientarme en este ejercicio?
(-6b^4) (1/4b^-6) (2/3b^7)
(-6b4)(1/4b-6)(2/3b7) = (-6∙1/4∙2/3)(b4+7/b6) =-b11–6 =-b5 (menos b elevado a 5)
1
–
X-⁶
Hola,
Aplicando las propiedades de las potencias, más concretamente la potencia del exponente negativo tenemos:
1
– = X⁶
X-⁶
=x6 (x elevado a 6)
Hola cómo resuelvo
m².m⁰
Hola,
Cualquier elemento elevado a 0 es igual a 1, así que m⁰=1 y por tanto m².1=m²
Hola buenas noches, podrías ayudarme con este ejercicio. Gracias
E= (7×2)²⁰ + 5¹⁵
———— ——–
49⁹x64³ 25⁷
[(-1)^2]^(3/2) puede dar 1 ó -1 en función de si haces primero el cuadrado o si aplicas potencia de una potencia…
Hola,
Éste es un caso particular. Si aplicas la potencia de una potencia te queda (-1)^(6/2), que efectivamente es igual a -1, pero no es la misma operación que [(-1)^2]^(3/2), ya que [(x)^2]^(3/2) y (x)^(6/2) no se corresponde a la misma función. Por tanto en este caso, hay que resolver potencias de dentro hacia afuera.
Un saludo
hola me podes explicar como se hacen las propiedades de las potencias
Me puede explicar división de potencias de bases distintas
Hola,
Lo tienes explicado en el Curso de Potencias
Saludos
Buenas Tardes me podria enviar 10 ejercicios sobre las propiedades de las potencias por favor 🙁
Hola profesor.
Espero pueda ayudarme.
Tengo entendido que no puede haber dos signos de operación juntos. En caso de la suma y resta se entiende que el primero es operación y el segundo es sentido.
Entonces si te go -(-3²) la base es de sentido negativo o el resultado de la potencia es de sentido negativo? Si es el segundo caso, entonces se estaría tomando ese segundo signo como de operación?
Hola,
Tienes que ir resolviendo las operaciones de dentro hacia afuera. Empezamos por la potencia que hay dentro del paréntesis. El signo menos que tiene delante no está afectado por la potencia. Para que estuviera afectado, entonces tendría que estar de esta forma (-3)². Resolvemos entonces la potencia, dejando el signo menos delante:
-(-3²)=-(-9)
Y ahora resolvemos los signos. Que haya un signo menos delante de un paréntesis es lo mismo que si se estuviera multiplicando por -1:
-(-9)=9
Saludos
-(-3 cuadrado) =-(-9) =9
Hola necesito ayuda como resuelvo esta potencia (3×(-5))²=
Hola,
Primero tienes que resolver la operación que tienes dentro del paréntesis y después resolver la potencia
Un saludo
(3x(-5))cuadrado =(-15)cuadrado =225
Saludos profesor, podría orientarme con esta duda por favor?
Porque la calculadora de Symbolab me arroja que (3^2-2^3)^66=1?
Asumiendo que lo hace primero resolviendo por separado cada potencia dentro del paréntesis y luego la potencia final;
(3^2-2^3)^66=
(9-8)^66=
1^66=
1
Sin embargo según la Propiedad de Potencia de otra Potencia debiese ser que el exponente de afuera multiplica a cada uno de los exponentes de adentro del paréntesis.
De forma que:
(a^m-b^n)^p=
a^m.p-b^n.p
Quedando;
3^2.66-2^3.66
Hola Miguel,
La propiedad de una potencia de otra potencia sólo se aplica cuando las potencias del interior del paréntesis se están multiplicando, por lo que la resolución correcta es resolviendo por separado cada potencia dentro del paréntesis y luego la potencia final, tal y como indicas en tu primer caso.
Saludos