A continuación te voy a explicar qué es la verdadera magnitud entre dos puntos en el sistema diédrico o lo que es lo mismo, cómo obtener la distancia entre dos puntos en el sistema diédrico. Lo veremos con todo detalle y con ejemplos resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Qué es la verdadera magnitud entre dos puntos en el sistema diédrico
La verdadera magnitud entre dos puntos es la distancia real que existe entre dos puntos en el espacio.
Cuando hallamos la verdadera magnitud entre dos puntos en el sistema diédrico, lo que hacemos obtener su distancia real en el espacio, pero con las proyecciones de dichos puntos.
Vamos a ver cómo hacerlo paso a paso en un esquema en tres dimensiones y luego veremos cómo hacer lo mismo en el sistema diédrico.
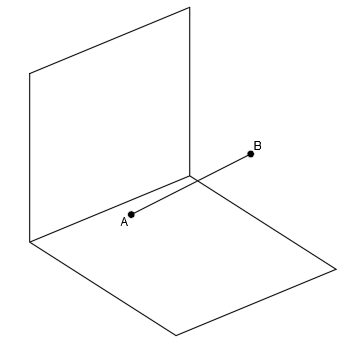
Tenemos en el espacio, sobre los planos de proyección, dos puntos A y B, unidos por una recta:
La recta que pasa por los puntos A y B no es paralela a ninguno de los planos de proyección, por tanto, sus proyecciones en cada plano están desvirtuadas y en ningún plano se observa la verdadera magnitud (distancia real) entre los dos puntos.
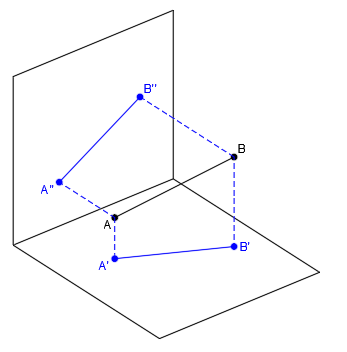
Las proyecciones de los puntos y de la recta en cada uno de los planos nos quedan de la siguiente forma:
Cuando una recta es paralela a alguno de los planos de proyección, en ese plano sí que se refleja en verdadera magnitud, puesto que la proyección de la recta coincide con la recta en el espacio. En ese caso, podemos medir la distancia directamente y no es necesario realizar el procedimiento que voy a explicar a continuación.
Seguimos con la recta del ejemplo.
Para obtener la verdadera magnitud entre dos puntos, lo que haremos será crear un triángulo rectángulo a partir de la recta que ya tenemos, para conseguir proyectar la recta en verdadera magnitud en uno de los planos de proyección.
Para ello, desde el punto A trazamos una recta paralela al plano de proyección horizontal, hasta la línea auxiliar de proyección del punto B al plano horizontal (punto A1), siendo perpendicular a dicha línea, por lo que nos queda un triángulo rectángulo en el espacio:
Nos queda un triángulo cuyos lados los nombramos como M, N y C:
Vamos a analizar cada uno de los lados del triángulo:
- El lado M es la hipotenusa del triángulo y corresponde con la distancia real entre los puntos A y B (o verdadera magnitud)
- El lado N es paralelo al plano horizontal y coincide con la proyección de la recta AB en dicho plano
- El lado C es la diferencia de cotas entre el punto A y el punto B, es decir, la diferencia de distancias al plano horizontal entre esos dos puntos. Además, el lado C es paralelo al plano vertical y perpendicular al plano horizontal.
Como el lado C es paralelo al plano vertical, la longitud de su proyección en el plano vertical coincide con la distancia real, por lo que en el plano vertical, la distancia entre los puntos B’ ‘ y A1’ ‘ está en verdadera magnitud:
Una vez tenemos el lado C en el plano vertical, podemos trasladar esa distancia al plano vertical, tranzando una recta perpendicular a la proyección horizontal de la recta desde el punto B, de longitud igual al lado C:
Nos queda dibujado el mismo triángulo que teníamos en el espacio, pero en el plano horizontal, donde la recta que pasar por A’ y B’ coincide con el lado N del triángulo en el espacio, el lado C, o hemos traslado a partir del plano vertical y por tanto, el lado que une A’ con (B) coincide con el lado M del espacio y por tanto, ya tenemos la verdadera magnitud entre el punto A y B.
Lo que acabos de hacer es equivalente a abatir el punto B hasta que el lado C sea paralelo al plano horizontal, por lo que todo el triángulo queda paralelo a ese plano y después proyectarlo. Por eso, llamamos así al punto (B) (B abatido):
Lo que debes entender de este procedimiento es que utilizamos el triángulo para obtener la diferencia de cotas entre los dos puntos, que se puede reflejar en verdadera magnitud en el plano vertical, para luego trasladar esa distancia al plano horizontal y poder formar el triangulo en este plano para poder medir su hipotenusa, que corresponde a la distancia real entre los dos puntos en el espacio.
Entenderás mejor este procedimiento cuando se aplique en el sistema diédrico, que es lo que veremos en el siguiente punto.
Cómo obtener la distancia real entre dos puntos en el sistema diédrico
Vamos a ver cómo hallar la distancia real, o verdadera magnitud ente dos puntos en el sistema diédrico, siguiendo el procedimiento explicado en el apartado anterior.
Tenemos los puntos A y B unidos por una recta representados en el sistema diédrico:
En el plano vertical, desde A’ ‘ trazamos una recta horizontal, paralela al plano horizontal y a la línea de tierra, hasta cortar con la línea de proyección vertical del punto B en el punto A1’ ‘:
Esta recta corresponde a la proyección vertical del lado N del triángulo.
La recta que pasa por los puntos A1′ ‘ y B’ ‘ corresponde al lado C del triángulo y la longitud de este lado es la diferencia de cotas entre los puntos A y B en verdadera magnitud:
Ahora, en el plano horizontal, trazamos una perpendicular a la recta A’B’, que pase por el punto B’ y tenga la longitud C, que la podemos trasportar con el compás:
Unimos los puntos A’ y (B), obteniendo la verdadera magnitud entre los puntos A y B:
Siguiendo un razonamiento similar, en vez de la diferencia de cotas, también podemos obtener la verdadera magnitud entre dos puntos utilizando la diferencia de alejamientos.
Vamos a ver un ejemplo. Tenemos dos puntos A y B unidos por una recta:
En el plano horizontal, desde A’ trazamos una recta horizontal, paralela al plano vertical y a la línea de tierra, hasta cortar con la línea de proyección vertical del punto B en el punto A1′. La longitud entre los puntos A1′ y B’ es la diferencia de alejamientos de los puntos A y B en verdadera magnitud:
En el plano vertical, trazamos una perpendicular a la recta A’ ‘B’ ‘, que pase por el punto B’ ‘ y tenga la longitud de A. Uniendo los puntos A’ ‘ y (B) obteniendo la verdadera magnitud entre los puntos A y B :
Ejemplo de verdadera magnitud entre dos puntos en diédrico
Vamos a aplicar lo aprendido hasta ahora para obtener la distancia real entre los siguientes dos puntos en diédrico:
En el plano vertical, desde A’ ‘ trazamos una recta paralela a la línea de tierra, hasta cortar con la línea de proyección vertical del punto B en el punto A1’ ‘:
Medimos la diferencia de cotas en verdadera magnitud, que corresponde a la longitud entre los punto A1′ ‘ y B’ ‘, cuyo valor es de 17,7 mm.
En el plano horizontal, trazamos una perpendicular a la recta A’B’, que pase por el punto B’ y de longitud 17,7 mm:
La distancia entre los puntos A’ y (B) corresponde a la verdadera magnitud de los puntos A y B, cuyo valor es de 68,89 mm:
Cómo obtener una distancia determinada sobre un segmento en diédrico
Supongamos que queremos obtener una distancia determinada sobre un segmento que une dos puntos.
¿Cómo lo haríamos?
En primer lugar, obtendríamos la verdadera magnitud de esos dos puntos y sobre ese segmento, marcaría un punto desde uno de los extremos, de la longitud que necesitara, para después tomar el camino inverso a obtener la verdadera magnitud y obtener la ubicación del punto.
Vamos a verlo paso a paso con un ejemplo.
Necesito obtener una distancia de 5o mm, del segmento que AB, tomada desde el punto A:
Obtengo la verdadera magnitud de estos dos puntos:
Ahora, sobre el segmento en verdadera magnitud, desde el punto A’, tomo una distancia de 50 mm, que será el punto (P). Todo lo que mida en ese segmento estará en verdadera magnitud:
Ahora sigo el camino inverso a hallar la verdadera magnitud.
Desde el punto (P), trazo una perpendicular al segmento A’B’. El punto de corte con ese segmento es el punto P’:
Finalmente, desde P’, trazo una vertical hasta cortar con el segmento A’ ‘B’ ‘, que será el punto P’ ‘:
Por tanto, ya tengo pasada al sistema diédrico una distancia de 50 mm, tomada desde el punto A, en el segmento AB, que corresponde a las proyecciones A’P’ y A’ ‘P’ ‘.
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE