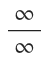A continuación te voy explicar qué es una indeterminación dentro del cálculo de límites y qué tipos de indeterminaciones existen.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué son las indeterminaciones
Las indeterminaciones en los límites son las expresiones que no quedan al sustituir la x por el número al que tiende y que no tienen solución.
En todas ellas, están involucradas de alguna forma el cero o el infinito.
Tipos de indeterminaciones
En función del tipo de indeterminación tendremos diferentes tipos de límites. Estos son los tipos de indeterminaciones que existen:
Infinito entre infinito
Dividir un número entre infinito es cero, pero si dividimos el propio infinito entre infinito ¿también es cero?
No, no tiene solución, por eso es indeterminado.
Cero entre cero
Algo similar al caso anterior ocurre con esta indeterminación. Sabemos que cero dividido entre cualquier número sigue siendo cero, pero si el cero lo dividimos entre cero, el resultado no es cero, es una indeterminación.
Un número entre cero
Un número dividido entre cero no tiene solución. Prueba a hacerlo con la calculadora y verás que te da error. Por tanto estamos ante otra indeterminación.
El resultado del límite cuando tenemos esta indeterminación puede ser infinito o menos infinito, pero a priori se desconoce.
Infinito menos infinito
¿Qué pasa si a infinito le restamos infinito? ¿El resultado es cero?
Infinito menos infinito no es cero, porque desconocemos el orden de magnitud de cada uno de los infinitos. No tienen porque ser igual de grandes. El infinito es un concepto muy abstracto y no tiene un valor definido. El ejemplo está en que podemos elevar infinito al cuadrado y sigue siendo infinito, mucho más infinito que antes.
Cero por infinito
Cuando multiplicamos un número por cero, el resultado es cero. Cuando multiplicamos un número entre infinito, el resultado es infinito. Pero, ¿qué pasa si multiplicamos cero por infinito? ¿El resultado es cero o es infinito?
Pues por eso mismo, el resultado es una indeterminación y no tiene solución.
Cero elevado a cero
Cualquier número elevado a cero es uno, pero por otro lado, cero por cero es cero. Entonces si cero lo elevamos a cero ¿es uno o es cero? Pues ni una cosa ni la otra. Es indeterminado.
Infinito elevado a cero
Esta indeterminación es parecida al caso anterior. ¿Qué pasa si elevamos infinito a cero? ¿El resultado es 1? No tiene sentido, por lo que el resultado es infinito.
Uno elevado a infinito
¿Cuánto es el resultado de multiplicar uno por uno infinitas veces? Se podría pensar que el resultado es uno, sin embargo, esta operación tampoco tiene solución.
Como ves, algunas de estas indeterminaciones pueden causar confusión por pensar que sí tienen solución.
Si quieres aprender a resolver límites con todos estos tipos de indeterminaciones te recomiendo que eches un vistazo al Curso de Límites, donde te explico cómo resolver límites paso a paso, con ejercicios resueltos.
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique paso a paso cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas desde cero conmigo? Pulsa el botón para saber más: