A continuación vamos a ver qué es la mediatriz de un segmento, cómo se realiza y cómo se utiliza para resolver ejercicios de geometría plana en dibujo técnico. Con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque no sabes resolver algún ejercicio de dibujo técnico y es muy probable que necesites clases de dibujo técnico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Dibujo Técnico Online:
VER CURSOS DE DIBUJO TÉCNICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar dibujo técnico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de dibujo técnico.
Qué es un lugar geométrico
Antes de empezar con la mediatriz, necesitas conocer el concepto de lugar geométrico.
Se llama lugar geométrico al conjunto de puntos que cumplen unas determinadas condiciones.
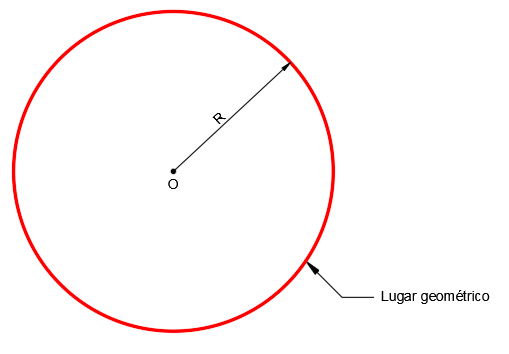
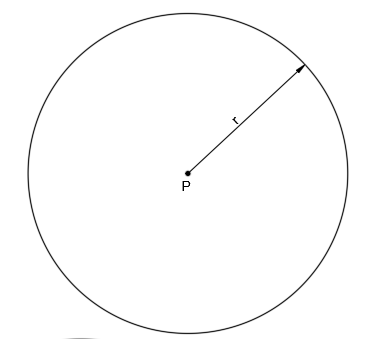
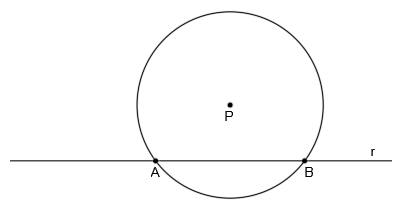
Por ejemplo, una circunferencia es el lugar geométrico cuyos puntos tienen la misma distancia R, a un punto fijo, O, donde O es el centro de la circunferencia y R es el radio:
Por tanto, cualquier punto que pertenezca a la circunferencia está a la misma distancia del centro O, concretamente a una distancia R.
Conocer la circunferencia como un lugar geométrico, nos ayudará a entender cómo se construye la mediatriz de un segmento y lo que es más importante, a entender sus propiedades.
Cómo trazar la mediatriz de un segmento
Vamos a ver cómo dibujar la mediatriz de un segmento paso a paso.
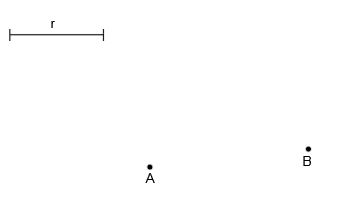
Tenemos el segmento AB:
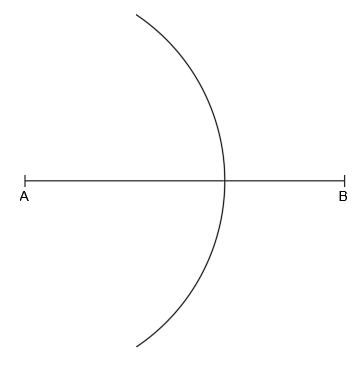
Con centro en A, dibujamos con el compás un arco de circunferencia, cuyo radio puedes ser cualquiera, con la única condición de que debe ser mayor a la mitad del segmento AB:
Teniendo en cuenta que las propiedades de la circunferencia como lugar geométrico, todos los puntos pertenecientes a este arco que acabamos de dibujar, están a la misma distancia del extremo A.
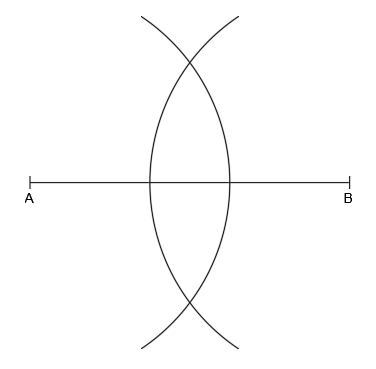
Con el mismo radio que dibujamos el arco con centro en A, dibujamos otro arco con centro en B:
Todos los puntos pertenecientes a este segundo arco, están a la misma distancia del extremo B.
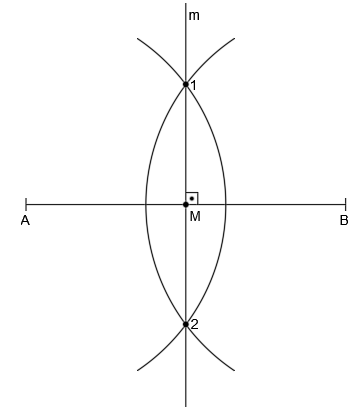
Los puntos de corte de ambos arcos (puntos 1 y 2) están a la misma distancia del extremo A y del extremo B, ya que son los puntos donde se cumplen las condiciones de ambos arcos, considerados como lugares geométricos:
La mediatriz será la recta m que pase por los puntos 1 y 2:
Corta al segmento en el punto M, que es el punto medio del segmento y por tanto también está a la misma distancia de ambos extremos y además la mediatriz es perpendicular al segmento.
Qué es la mediatriz de un segmento
Normalmente se dice que la mediatriz de un segmento es la recta que corta al segmento por su punto medio y que además es perpendicular al segmento, tal y como acabamos de ver:
Sin embargo, de esta definición concluimos que al mediatriz es perpendicular al segmento y que lo corta en dos partes iguales, pero nos falta más información, como veremos a continuación.
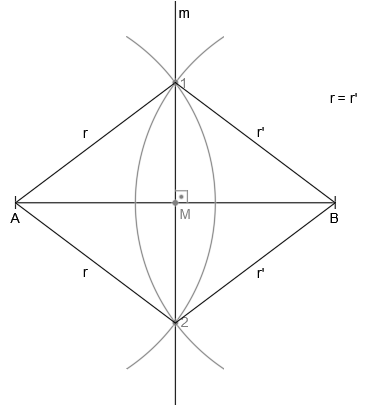
Como he comentado antes, los puntos 1 y 2 se encuentran a la misma distancia de los extremos A y B, es decir, en el siguiente dibujo, los segmentos r y r’ tienen la misma longitud:
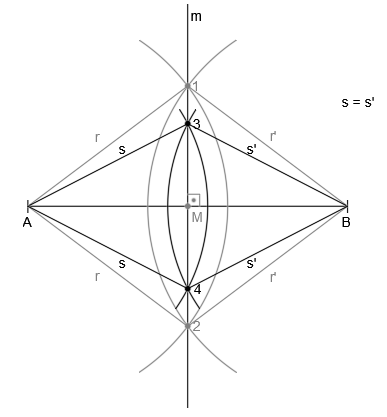
Si trazáramos de nuevo un arco de circunferencia desde cada extremo, con el mismo radio, mayor que la mitad del segmento, pero distinto al anterior, vemos que los arcos se cortan en los puntos 3 y 4:
Los puntos 3 y 4, también pertenecen a la mediatriz y por tanto, están a la misma distancia de los extremos A y B.
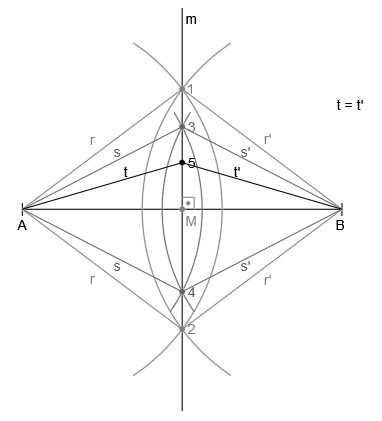
De todo esto se deduce que cualquier punto que pertenezca a la mediatriz está a la misma distancia de los extremos del segmento. Si tomamos un punto cualquiera (punto 5), vemos que efectivamente es equidistante a los extremos A y B, o dicho de otra forma, la longitud de los segmentos t y t’ son iguales::
Por tanto, la mediatriz también se puede definir como el lugar geométrico, en el cual los puntos que pertenezcan a él tienen la misma distancia a los extremos del segmento y como consecuencia, es el lugar geométrico de los centros de las circunferencias que pasan por los puntos A y B:
Y esta definición de mediatriz como lugar geométrico es la que nos ayudará a resolver ejercicios más complejos de geometría plana.
Mediatriz: Ejercicios resueltos
Vamos a ver cómo resolver algunos ejercicios con lo aprendido en esta lección:
Ejercicio 1
Hallar el lugar geométrico de los puntos del plano que distan una distancia r de un punto dado P.
El lugar geométrico de los puntos del plano que tienen la misma distancia a un punto es la circunferencia, así que la solución del ejercicio es una circunferencia de radio r con centro en P:
Ejercicio 2
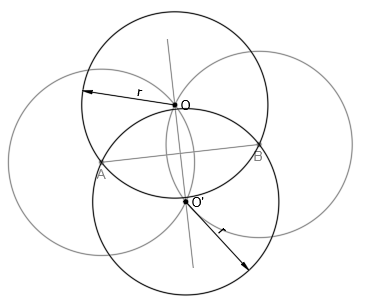
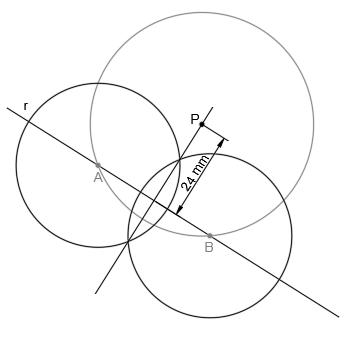
Hallar el lugar geométrico de los centros de las circunferencias de radio r que pasen por un punto fijo P:
Ya sabemos que la circunferencia es el lugar geométrico donde los puntos tienen la misma distancia a un punto fijo, así que si la solución es la circunferencia con centro en P y de radio r, ya que si trazamos varias circunferencias de radio r, con centro en la circunferencia que ya tenemos, todas pasarán por el punto P:
Ejercicio 3
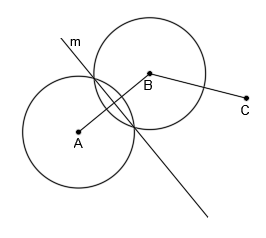
Trazar las circunferencias de radio r que pasen por dos puntos dados A y B:
El centro de las circunferencias que pasen por A y B, debe estar a la misma distancia de ambos puntos y el lugar geométrico de los puntos que están a la misma distancia de dos puntos es la mediatriz.
Por otra parte, el lugar geométrico de los puntos que distan una distancia r de cada punto es una circunferencia con centro en cada punto y de radio R.
Así que trazamos la mediatriz del segmento que une los puntos A y B, utilizando para ello circunferencias de radio r:
Los puntos donde se cortan ambas circunferencias, además de ser los puntos por donde pasará la mediatriz, serán los puntos de los centros de las circunferencias de radio r que pasen por A y por B, ya que son los puntos que cumplen donde se cumplen las condiciones de estar a la distancia r de A y B:
Este ejercicio sólo tiene solución si el radio dado es mayor a la mitad de la distancia entre A y B.
Otra forma de hacerlo sería obtener la mediatriz del segmento que pasa por A y B, con una circunferencia de radio cualquiera y después, hallar los centros O y O’ trazando una circunferencia de radio r con centro en A o en B. Los puntos de corte de esta circunferencia con la mediatriz serían los centros buscados ya que son los puntos donde se unen las condiciones de estar a la misma distancia de A y B (por la mediatriz) y estar a una distancia r (por la circunferencia).
Ejercicio 4
Trazar la perpendicular a una recta dada r que pase por un punto P de la misma:
Sabemos que la mediatriz es la recta perpendicular a un segmento y que pasa por su punto medio.
En este ejercicio no tenemos ningún segmento, así que tenemos que crearlo. Para ello, con centro en P trazamos una circunferencia con radio cualquiera. Los puntos de corte de la circunferencia con la recta serán los puntos A y B:
Podemos considerar la recta A y B como un segmento y además, ya tenemos su punto medio P, por lo que si trazamos la mediatriz de este segmento pasará por P y ya tendremos la solución del ejercicio:
Ejercicio 5
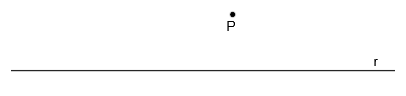
Trazar la perpendicular a una recta dada r que pase por un punto exterior P:
De nuevo sabemos que la mediatriz es la recta perpendicular a un segmento, pero no tenemos ningún segmento.
Así que creamos un segmento, trazando una circunferencia con centro en P, de radio lo suficientemente grande para que corte a la recta en dos puntos, A y B, que serán los puntos de nuestro segmento:
Al haber trazado una circunferencia con centro en P, sabemos que P está a la misma distancia de A y de B y por tanto, pertenecerá a la mediatriz, así que si trazamos la mediatriz de nuestro segmento A y B, pasará por el punto P:
Ejercicio 6
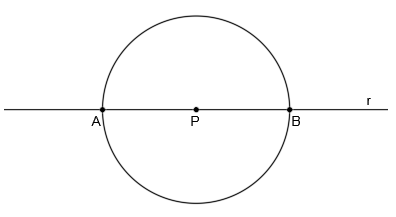
Hallar la distancia del punto P a la recta r:
La distancia de un punto a una recta es el segmento que une el punto con la recta y que es perpendicular a la recta.
Así que, tenemos que trazar la recta que pase por el punto P y sea perpendicular a r, siguiendo el mismo procedimiento que el ejercicio anterior.
Trazamos una circunferencia con centro en P que corte a la recta r, que serán los puntos A y B:
Trazamos la mediatriz del segmento A y B, que pasará por P. La distancia medida en la mediatriz desde P hasta la recta es la distancia del punto a la recta:
Ejercicio 7
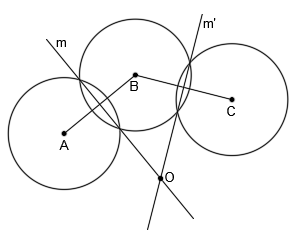
Hallar la circunferencia que pase por tres puntos dados no alineados A, B y C:
Para que una circunferencia pase por los puntos A y B, su centro debe estar a la misma distancia de esos dos puntos, es decir, su centro pertenece a la mediatriz del segmento que une los puntos A y B, así que trazamos la mediatriz m del segmento A y B:
Cualquier circunferencia que tenga centro en un punto de la mediatriz m y tenga el radio igual a la distancia desde ese punto al punto A o al punto B pasará por dichos puntos.
Pero nos falta que pase también por el punto C.
Así que trazamos la mediatriz del segmento que une los puntos B y C.
De la misma forma, cualquier circunferencia que tenga centro en un punto de la mediatriz mi y tenga el radio igual a la distancia desde ese punto al punto B o C, pasará por dichos puntos.
En el punto de corte de ambas mediatrices (punto O), se unen ambas condiciones, es decir, está a la misma distancia de A, B y C:
Por tanto, una circunferencia con centro en O y de radio igual a la distancia desde O a cualquiera de los tres puntos es la circunferencia solución del ejercicio:
¿Necesitas clases de dibujo técnico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de dibujo técnico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de dibujo técnico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de dibujo técnico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el dibujo técnico. ¿Quieres informarte de como puedes aprender dibujo técnico? Pulsa el botón para saber más: