A continuación vamos a estudiar la monotonía de una función, es decir, cómo saber si una función es creciente o decreciente, así como los extremos relativos de una función, o lo que es lo mismo, cómo identificar sus máximos y sus mínimos, a partir de su gráfica.
Veremos los conceptos más importantes y realizaremos ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Monotonía de una función
¿Qué es la monotonía de una función?
La monotonía de una función indica los intervalos donde la función crece, decrece o se mantiene constante.
Crecimiento de una función
Decimos que una función crece en un determinado intervalo, si cuando nos movemos en el sentido positivo del eje x (hacia la derecha), el valor de la función aumenta.
Es decir, que para cualquier par de valores dentro de un intervalo, donde x2 sea mayor que x1, el valor de la función cuando x=x2 es mayor que el valor de la función cuando x=x1:
Gráficamente, queda representado de la siguiente manera:
Donde f(x2) es mayor que f(x1) (mirando el eje y).
Una función puede tener intervalos de crecimiento o ser creciente en todo su dominio, que en ese caso, se dice que la función es estrictamente creciente, ya que el valor de la función es mayor cuanto mayor sea el valor de x.
Derecimiento de una función
Decimos que una función decrece en un determinado intervalo, si cuando nos movemos en el sentido positivo del eje x (hacia la derecha), el valor de la función disminuye.
Es decir, que para cualquier par de valores dentro de un intervalo, donde x2 sea mayor que x1, el valor de la función cuando x=x2 es menor que el valor de la función cuando x=x1:
La representación gráfica de un intervalo de decrecimento sería:
Donde f(x2) es menor que f(x1).
Una función puede tener intervalos de decrecimiento o ser decreciente en todo su dominio, que en ese caso, se dice que la función es estrictamente decreciente, ya que el valor de la función es menor cuanto mayor sea el valor de x.
Funciones constantes
Por último, si el valor de la función no varía para cualquier valor de x, decimos que la función es constante. En este caso, para cualquier valor de x, el valor de la función siempre es el mismo:
Una función constante tiene la siguiente forma:
Donde como vemos, tanto para x1 como para x2, el valor de la función es el mismo.
Extremos relativos de una función
Se le llama extremos relativos de una función a los valores más grandes o más pequeños que toma la función dentro de un determinado región o entorno (más abajo entenderás a lo que me refiero con región o entorno. A los valores más grandes de la función se le llaman máximos y a los más pequeños se le llaman mínimos.
Vamos a ver cada uno de ellos más despacio.
Máximo relativo de una función
Decimos que una función tiene un máximo relativo en X0, si existe un entorno alrededor de X0, tal que para cualquier valor de x, el valor de la función cuando x=X0 es mayor que para cualquier valor de x de ese entorno:
El entorno alrededor de X0, son los valores de x cercanos a X0, tanto por la izquierda como por la derecha.
Representado gráficamente, vemos claramente como a X0, le corresponde el mayor valor de la función:
Teniendo en cuenta que Y0=f(X0):
también podemos decir que tenemos un máximo en (X0,Y0).
Mínimo relativo de una función
Por otro lado, decimos que una función tiene un mínimo relativo en X0, si existe un entorno alrededor de X0, tal que para cualquier valor de x, el valor de la función cuando x=X0 es menor que para cualquier valor de x de ese entorno:
Que representado gráficamente queda:
Donde vemos que en X0, el valor de la función es menor que para cualquier valor de x de su entorno.
Para indicar el mínimo, también podemos decir que hay un mínimo en el punto (X0,Y0).
Ejemplo sobre monotonía y extremos de una función
Vamos a ver paso a paso con un ejemplo todo lo que te acabo de explicar para que lo veas mucho más claro.
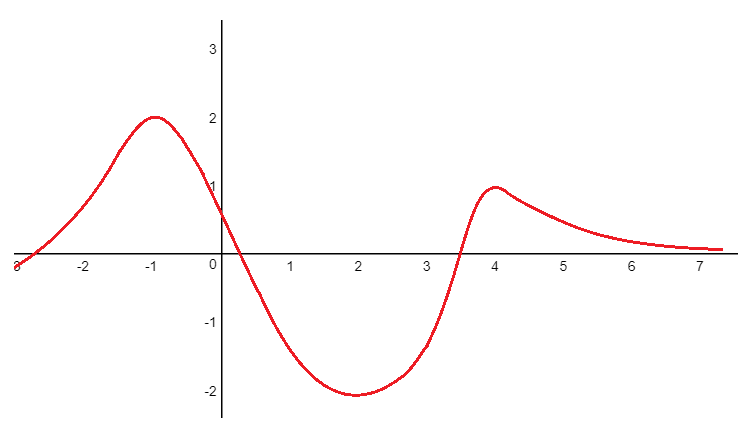
En la siguiente función, vamos a indicar los intervalos de crecimiento y decrecimiento, así como los extremos relativos:
Empezamos con los intervalos de crecimiento, que son los que van hacia arriba, conforme nos movemos a la derecha en el eje x. Los marco en azul para que los identifiques mejor:
Tanto los intervalos de crecimiento como los intervalos de crecimiento son intervalos abiertos, es decir, van entre paréntesis y se expresan de izquierda a derecha, con los valores de x separados por comas.
Tenemos dos intervalos de crecimiento. El primero va desde menos infinito hasta -1:
Y el segundo desde 2 hasta 4:
Seguimos con los intervalos de decrecimiento, que son los que van hacia abajo, conforme nos movemos a la derecha en el eje x. Los marco en azul:
Tenemos dos intervalos de decrecimiento, el primero va desde -1 hasta 2:
Y el segundo va desde 4 hasta infinito:
Por último vamos a indicar los extremos relativos.
Vemos que hay un máximo en el punto (-1,2), un mínimo en el punto (2,-2) y otro máximo en el punto (4,1). También podemos decir que hay un máximo en x=-1, un mínimo en x=2 y un máximo en x=4:
Aunque se expresen igual, no debes confundir las coordenadas de los puntos de los extremos relativos con los intervalos de crecimiento y decrecimiento, ya que en el caso de los intervalos, lo que indicamos entre paréntesis son dos valores de x y en el caso de los extremos, indicamos la coordenada x y la coordenada «y» de un punto.
Ejercicios resueltos sobre monotonía y extremos relativos de una función a partir de su gráfica
Ejercicio resuelto 1
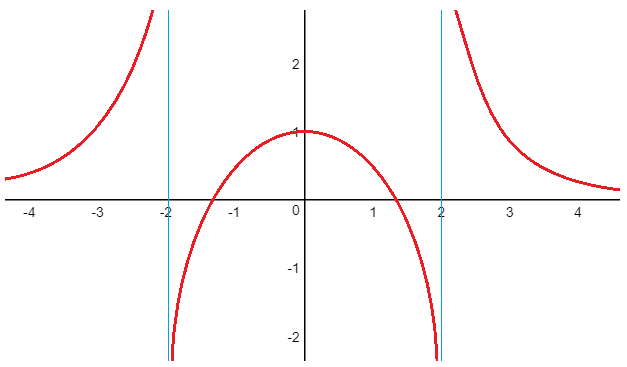
Analiza y estudia en la siguiente función el dominio, la imagen, la monotonía y los extremos relativos:
El dominio y la imagen de una función las tienes explicadas en sus correspondientes lecciones del Curso de Funciones.
Dominio: Dom f=R-{-2,2}
Imagen: Im f=R
Monotonía: La función es creciente en los intervalos (-∞,-2) y (-2,0) y decreciente en los intervalos (0,2) y (2,∞)
Extremos: Tiene un máximo en (1,0)
Ejercicio resuelto 2
Dibuja la gráfica correspondiente a la función con las características que se citan a continuación:
a) Dom f=(-∞,1) U (1,∞); Im f=R ; máximos en los puntos (-2,2) y (3,1) y mínimo en el punto (0,-1)
b) Dom f=R; Im f=(-3,2); mínimo en el punto (-2,-1) y máximo en el punto (0,1)
Ejercicios propuestos
1- Analiza y estudia en la siguiente función el dominio, la imagen, la monotonía y los extremos relativos:
2- Dibuja la gráfica correspondiente a la función con las características que se citan a continuación:
a) Dom f=(-∞,0); Im f=(1,∞) y estrictamente creciente en todo el dominio
b) Dom f=R-{0}; Im f=(0,∞); creciente en (-∞,0) y decreciente en (0,∞)
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: