A continuación vamos a ver cómo realizar operaciones con ángulos en geometría, es decir, de forma gráfica con ayuda de una regla y un compás. Te explicaré cómo realizar sumas, restas y multiplicaciones de ángulos de gráficamente. Previamente te enseñaré cómo trasladar ángulos. Todo con ejemplos resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es porque no sabes resolver algún ejercicio de dibujo técnico y es muy probable que necesites clases de dibujo técnico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte a los Cursos de Dibujo Técnico Online:
VER CURSOS DE DIBUJO TÉCNICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar dibujo técnico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de dibujo técnico.
Traslación de ángulos
Antes de ver cómo realizar operaciones con ángulos en geometría, tienes que aprender el concepto de traslación de ángulos.
Trasladar un ángulo es construir un ángulo igual a otro que ya tenemos pero en un lugar diferente del plano.
Vamos a ver un ejemplo
Ejemplo de cómo trasladar un ángulo ángulos
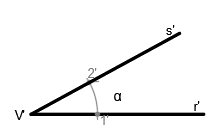
Tenemos el siguiente ángulo α, formados por las rectas r y s que se cortan en el vértice V:
Vamos a trasladar este ángulo, al que llamaremos ángulo dado para referirnos a él.
Empezamos trazando una paralela a r, que será r’, donde uno de sus extremos será el vértice del triángulo V’:
En el ángulo dado, trazamos un arco de circunferencia, con centro en V y de un radio cualquiera, que cortará a las rectas r y s en los puntos 1 y 2 respectivamente. Con el mismo radio, dibujamos otro arco en el ángulo que estamos construyendo, con centro en V’, que corta a r’ en el punto 1′:
Ahora, en el ángulo dado, con centro en el punto 1, abrimos el compás hasta el punto 2 y hacemos un pequeño arco para comprobar que corta en el punto 2. Sin mover el compás, nos vamos al ángulo que vamos a trasladar y con centro en el punto 1′, trazamos un pequeño arco que corte al arco que ya tenemos. El punto de corte de ambos arcos será el punto 2′:
En el ángulo a construir, trazamos la recta s’ que pase por los puntos V’ y 2′:
Y ya tenemos nuestro ángulo:
Básicamente lo que hemos hecho con ayuda del compás es medir la apertura del ángulo y para eso hemos trazado un arco como referencia que cortara a ambas rectas.
Suma de ángulos con compás
Vamos a ver ahora cómo sumar ángulos gráficamente con el compás.
Tenemos los siguientes dos ángulos los cuales queremos sumar:
Para realizar la suma gráfica de ángulos, necesitamos saber cómo realizar la traslación de ángulos, que lo hemos aprendido en el apartado anterior.
En primer lugar trasladamos el ángulo α.
Trazamos r’, que es paralela a r y a uno de los extremos lo llamamos V», que será el vértice del ángulo. Sobre el ángulo dado trazamos un arco de radio cualquiera, que corte a las rectas r y s en los puntos 1 y 2 y con el mismo radio, trazamos otro arco en la recta r’ con centro en V».
Esta vez, dibuja el arco en el ángulo a trasladar de una longitud suficiente para que nos quepa el siguiente ángulo, tal y como hago yo en el siguiente dibujo:
En el ángulo dado, con centro en 1, trazamos un arco de radio igual a la distancia que hay de 1 a 2 y con el mismo radio, en el ángulo a construir trazamos un pequeño arco que corte en el punto 2′ al arco realizado en el paso anterior:
Unimos los puntos V» y 2′ para trazar la recta s’, para terminar de dibujar el ángulo α:
Ahora, a este ángulo, vamos a sumarle gráficamente el ángulo β, trasladando este ángulo β sobre el ángulo α que acabamos de construir, es decir, la recta s’ será la equivalente a la recta t del ángulo β.
Para ello, en el ángulo β dado, con centro en V’, trazamos un arco, de radio igual al arco que realizamos en el ángulo α con centro en V, que corte a las rectas t y u en los puntos 3 y 4:
Como en los ángulos que estamos construyendo ya dibujamos el arco con una longitud suficiente no tenemos que hacer nada en este.
Con centro en el punto 3, trazamos un pequeño arco de radio igual a la longitud entre 3 y 4 y sin mover el compas, es decir, con el mismo radio, vamos a los ángulos que estamos sumando y con centro en 2′ trazamos otro pequeño arco que cortará al arco que ya teníamos en el punto 4′:
Acabamos de llevarnos la amplitud del ángulo β encima del ángulo α.
Por último, trazamos la recta u’, uniendo los puntos V» y 4′:
Y ya tenemos el ángulo γ, que es el resultado de realiza la suma gráfica de los ángulos α y β:
Para resumir, lo que hemos hecho es trasladar el ángulo α y después, sobre este, trasladar el ángulo β.
Resta de ángulos con compás
Vamos a ver ahora cómo realizar la resta gráfica de ángulos, cuyo procedimiento es muy parecido al apartado anterior, pero con una pequeña diferencia.
En este caso, también vamos a realizar dos traslaciones de ángulo, pero esta vez, uno de ellos será en sentido contrario.
Vamos a ver cómo realizar la resta de ángulos con compás paso a paso.
Tenemos los siguientes ángulos:
Al ángulo α (ángulo mayor) le vamos a restar el ángulo β (ángulo menor).
En primer lugar, trasladamos el ángulo α
Trazamos r’, paralela a r y con centro en V, trazamos un arco de radio cualquiera y con el mismo radio, trazamos otro arco en la recta r’ con centro en V»:
En el ángulo dado, con centro en 1, trazamos un arco con radio igual a la longitud de 1 a 2 y trazamos el mismo arco con centro en 1′, que cortará al arco que ya tenemos en el punto 2′:
Unimos los puntos V» y 2′ para trazar s’ y terminar de trasladar el ángulo α:
Ahora, sobre la recta s’ de este ángulo, vamos a trasladar el ángulo β, pero en sentido contrario al ángulo dado.
Para ello, en el ángulo β, trazamos un arco de radio igual al arco que trazamos con centro en V en el ángulo α, que cortará a las rectas t y u en los puntos 3 y 4:
En el ángulo que estamos construyendo no tenemos que hacer nada porque ya tenemos el arco que necesitamos.
En el ángulo β dado, esta vez con centro en el punto 4, trazamos un arco que tenga un radio igual a la distancia entre los puntos 3 y 4 (hubiera dado igual hacerlo en el otro sentido porque lo que queremos es tener la amplitud del ángulo). En el ángulo a construir, con centro en 2′ trazamos un arco que corte al ángulo que ya tenemos en el punto 3′ (en este caso, si es importante que el ángulo esté en sentido contrario al ángulo dado):
Trazamos una recta uniendo los puntos V» y 3′ para cerrar el ángulo γ, que es el resultado de restar α menos β:
Multiplicación de ángulos con compás
Por último, vamos a ver cómo realizar la multiplicación gráfica de ángulos con ayuda del compás, paso a paso.
Tenemos el siguiente ángulo α:
Vamos a realizar gráficamente la multiplicación del ángulo α por 3, es decir, 3α
Para ello, empezamos trasladando el ángulo alfa, siguiendo el procedimiento de siempre. En este caso, el arco que realices en el ángulo a construir, asegúrate que tiene una longitud suficiente para que quepan más ángulos (tres concretamente):
Medidos con el compás la amplitud de α y ahora y sin cerrar el compás, es decir, con el mismo radio, con centro en 1′, trazamos un arco que cortará al arco dibujado anteriormente en el punto 2′ y realizamos los mismo 2 veces más, pero cambiando de centro, es decir, con centro en 2′, trazamos otro arco, consiguiendo el punto de corte 3′ y con centro en 3′, hallamos el punto de corte 4′ con otro arco:
Trazamos tres rectas uniendo los puntos 2′, 3′ y 4′ con el vértice V»:
Nuestro ángulo γ=3α es el formado por las rectas r’ y u’:
Lo que hemos hecho en este caso para multiplicar ángulos gráficamente es trasladar el ángulo α tres veces, uno a continuación de otro, es decir, hemos realizado la suma de α+α+α.
¿Necesitas clases de dibujo técnico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de dibujo técnico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de dibujo técnico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de dibujo técnico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el dibujo técnico. ¿Quieres informarte de como puedes aprender dibujo técnico? Pulsa el botón para saber más: