A continuación te voy a explicar el paralelismo en el sistema diédrico, es decir, cómo trazar una recta paralela a otra, una recta paralela a un plano, un plano paralelo a una recta y un plano paralelo a otro plano. Todo con ejercicios resueltos paso a paso.
¡Empezamos!
Si has llegado hasta aquí es no entiendes el sistema diédrico y es muy probable que necesites clases de sistema diédrico online. Si después de leer esto, quieres seguir aprendiendo paso a paso y desde cero, en una plataforma donde tengas todo explicado, con ejercicios resueltos y alguien que te resuelva tus dudas, solo tienes que apuntarte al Curso de Sistema Diédrico Online:
VER CURSO DE SISTEMA DIÉDRICO ONLINE
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar sistema diédrico. Puedo explicarte paso a paso cualquier duda que no entiendas.
Sólo tienes que dejarte guiar y verás como vas a aprendiendo poco a poco a resolver tus ejercicios de sistema diédrico.
Cómo trazar una recta paralela a otra en el sistema diédrico
Vamos a empezar viendo cómo dibujar una recta paralela a otra recta dada y que pase por un punto:
Las proyecciones cilíndricas ortogonales de dos rectas paralelas en el espacio son también paralelas:
Como el sistema diédrico utiliza proyecciones cilíndrico ortogonales en dos planos, podemos decir que dos rectas son paralelas cuando sus proyecciones son paralelas.
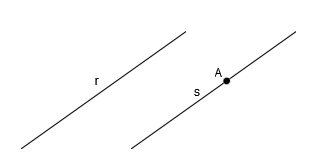
Por ejemplo, las rectas r y s, representadas en diédrico, son paralelas porque r’ ‘ es paralela a s’ ‘ y r’ es paralela a s’:
Sabiendo esto, vamos a ver cómo trazar una recta paralela a otra dada y que pase por un punto en el sistema diédrico.
El procedimiento para trazar una recta a otra que pase por un punto es el siguiente:
- Trazar la proyección vertical de la recta, s’ ‘, paralela a r’ ‘ y que pase por la proyección vertical del punto A’ ‘
- Trazar la proyección horizontal de la recta, s’, paralela a r’ y que pase por la proyección horizontal del punto A’
Ejercicio resuelto
Por ejemplo, tenemos la recta r y el punto A. Dibujar la recta paralela a la recta r que pase por A:
La recta que dibujemos será paralela a la recta dada sólo si las dos proyecciones de la recta son paralelas a las proyecciones de la recta dada. Por tanto, en primer lugar, dibujamos s’ ‘, paralela a r’ ‘ y que pase por el punto A’ ‘:
Después dibujamos s’, paralela a r’ y que pase por el punto A’:
Y ya tenemos la recta s, que es paralela a r, ya que sus proyecciones son paralelas.
Trazas de las rectas paralelas en diédrico
Puede pensarse que dos rectas paralelas en el sistema diédrico deben tener las trazas iguales, pero eso no tiene por qué ser así. Las trazas sólo serán iguales cuando la recta esté a la misma altura en el espacio con respecto a los planos de proyección.
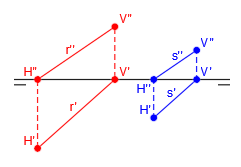
También puede darse el caso de dos rectas paralelas cuyas trazas sean distintas, como en el siguiente esquema, donde podemos observar que la recta s, se encuentra más cerca de los planos de proyección que la recta r:
Si las representamos en el sistema diédrico nos quedarían de la siguiente forma:
Como puedes comprobar, las rectas r y s son paralelas, siendo sus trazas son distintas.
Cómo dibujar una recta paralela a un plano por un punto en diédrico
Vamos a ver ahora cómo trazar una recta paralela a un plano y que pase por un punto en el sistema diédrico.
Para que una recta sea paralela a un plano, tiene que serlo a una de las infinitas rectas contenidas en el plano. Por tanto, si queremos trazar una recta paralela a un plano por un punto, en primer lugar tomaremos una recta de dicho plano y después trazaremos una recta paralela a dicha recta que pase por el punto dado.
Vamos a ver el procedimiento más despacio
Tenemos en el espacio el plano α y el punto A:
Primero trazamos una recta que esté contenida en el plano (recta r):
Trazamos una recta paralela a r y que pase por el punto A
Ejercicio resuelto
Tenemos el plano α y el punto A representados en diédrico. Dibujar la recta paralela al plano α que pase por A:
En primer lugar, debemos dibujar una recta cualquier que esté contenida en el plano α.
Para ello, dibujamos una proyección vertical cualquiera de la recta r:
Obtenemos las trazas V’ ‘ , en el punto de corte de la recta y plano y H’ ‘, en el punto de corte de la recta y la línea de tierra:
Obtenemos las trazas V’, trazando una línea vertical desde V’ ‘ hasta cortar con la línea de tierra y H’, trazando una línea vertical desde H’ ‘ hasta cortar con la traza horizontal del plano α1:
Unimos V’ y H’ para obtener la proyección horizontal de la recta r’:
Ya tenemos la recta r, contenida en el plano α. Ahora dibujamos una recta paralela a r, que pase por el punto A, es decir, s’ ‘ es paralela a r’ ‘ y pasa por A’ ‘ y s’ es paralela a r’ pasando por A’:
La recta s es paralela al plano α, que es lo que estamos buscando, al ser paralela a una recta contenida en el plano.
Este ejercicio también puede resolverse utilizando rectas horizontales o rectas frontales, como recta contenida en el plano.
En este caso lo vamos a resolver con una recta horizontal contenida en el plano.
Tenemos el plano y el punto:
Dibujamos la recta r, una recta horizontal contenida en el plano:
Ahora vamos a dibujar la recta s paralela a r. Para ello, primero dibujamos la proyección s’, paralela a r’ y que pase por el punto A’.
La proyección s’ ‘ es paralela a r’ ‘ y a la línea de tierra y pasa por el punto A’ ‘, llegando hasta V’ ‘, que se obtiene de la línea vertical trazada partir de V’:
Ésta sería otra recta s, paralela al plano. Solución distinta a la anterior (realmente este ejercicio tiene infinitas soluciones, al ser infinitas las rectas que pueden estar contenidas en el plano).
Cómo obtener un plano paralelo a una recta por un punto en el sistema diédrico
El procedimiento para trazar un plano paralelo a una recta que pasa por un punto es el siguiente:
- Trazamos una recta paralela a la recta dada, que pase por el punto dado
- Hallamos las trazas de la nueva recta
- Trazamos un plano que contenga a la nueva recta. Este plano, por contener a la recta paralela a la dada, también será paralelo a la recta dada.
Vamos a verlo más despacio con un ejercicio resuelto.
Ejercicio resuelto
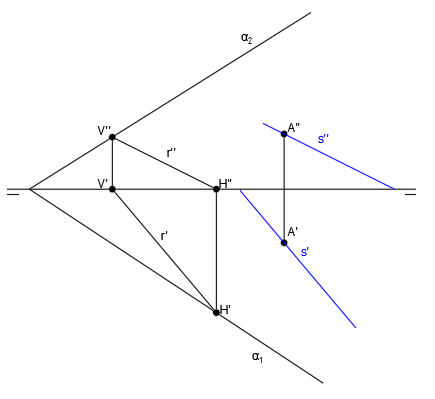
Tenemos la recta r y el punto A en el sistema diédrico. Dibujar un plano paralelo a la recta r:
Trazamos la recta s, paralela a r, que pase por el punto A. Las proyecciones de s serán paralelas a las de r, pasando por su correspondiente proyección del punto:
Obtenemos las trazas de la recta s:
Trazamos un plano cualquiera que contenga a la recta s. Para ello, la traza vertical del plano, pasa por la traza V’ ‘ de la recta s y la traza horizontal del plano, pasa por la traza de la recta H’, uniéndose ambas trazas en el mismo vértice:
El plano α trazado es paralelo a la recta r.
Cómo trazar un plano paralelo a otro por un punto en diédrico
Finalmente, vamos a ver cómo trazar un plano paralelo a otro por un punto en diédrico. El procedimiento a seguir es el siguiente:
- Trazamos una recta horizontal o frontal paralela al plano α, es decir, con su traza oblicua paralela a la traza del plano que corresponda, que pase por el punto dado y su otra traza paralela a la línea de tierra y que también pase por el punto, hasta su traza.
- Una traza del plano es paralela a la proyección de la recta, pasando por la traza de la recta
- La otra traza del plano es paralela a la traza del plano dado, pasando por el punto de corte de la traza del paso anterior con la línea de tierra.
Ejercicio resuelto
Tenemos el plano α y el punto A en el sistema diédrico. Dibujar un plano paralelo al plano α:
En este caso vamos a solucionar el ejercicio con una recta frontal.
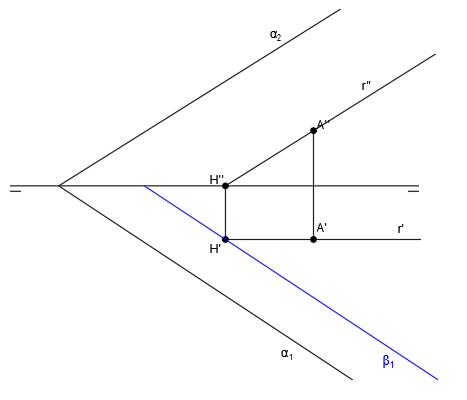
Dibujamos la proyección de la recta r’ ‘, paralela a α2 y que pase por el punto A’ ‘:
La proyección r’ es paralela a la línea de tierra y pasa por el punto A’, llegando hasta H’, que se obtiene de la línea vertical trazada partir de H’ ‘:
Ya tenemos la recta r, que es paralela al plano α. Ahora vamos a dibujar un plano β que la contenga y ese plano β será paralelo al plano α.
Dibujamos la traza horizontal del plano β1, paralela a la traza α1 y que pase por H’:
La traza vertical del plano β2, la dibujamos paralela a α2 y a r’ ‘, desde el punto donde β1 corta a la línea de tierra, que es el vértice del plano:
El plano β es paralelo al plano α.
¿Necesitas clases de sistema diédrico? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para entender cualquier concepto de sistema diédrico.
He diseñado un método práctico y efectivo que te ayudará a entender cómo resolver ejercicios de sistema diédrico, paso a paso, explicándote justo lo que necesitas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios de sistema diédrico y lo más importante, sabrás por qué se dan esos pasos.
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando información por Internet si puedes aprenderlo en menos de 20 minutos?
Te explicaré lo que necesitas aprender para entender el sistema diédrico. ¿Quieres informarte de como puedes aprender sistema diédrico? Pulsa el botón para saber más:
VER CURSO DE SISTEMA DIÉDRICO ONLINE