A continuación te explico qué son las permutaciones ordinarias, la permutaciones circulares y las permutaciones con repetición. Veremos también cómo se calcula cada una de ellas y resolveremos ejercicios sobre permutaciones.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Permutaciones ordinarias
Las permutaciones ordinarias de n elementos son los diferentes grupos que se pueden formar con esos n elementos.
En las permutaciones ordinarias:
- SÍ intervienen todos los elementos
- SÍ IMPORTA el orden de los elementos
- NO se pueden repetir los elementos
La diferencia entre las permutaciones y las variaciones es que en las permutaciones intervienen todos los elementos.
La fórmula para calcular las permutaciones ordinarias es:
Por ejemplo, ¿de cuántas maneras se pueden distribuir 7 tareas entre 7 empleados?
En este caso tenemos una permutación ordinaria de 7 elementos, ya que intervienen los 7 elementos, importa el orden, ya que todas las tareas no son iguales y los elementos no se pueden repetir, ya que los empleados y las tareas son diferentes.
Por tanto, aplicamos la fórmula de la permutación ordinaria y queda:
Se podrían distribuir de 5040 formas distintas.
Permutaciones circulares
Cuando los elementos se ordenan formando un círculo, estamos ante un caso particular de la permutación ordinaria, que es la permutación circular.
Vamos a verlo con un ejemplo: ¿De cuántas formas posibles se pueden sentar 5 personas en una mesa circular.
Si te preguntaran que de cuántas formas de pueden sentar cinco personas en cinco sillas situadas en fila, entonces estaríamos ante una permutación ordinaria y el resultado sería:
Ahora bien, al estar las sillas situadas en una mesa circular, por ejemplo, una vez sentados, pueden moverse todos de silla hacia la derecha y y cada uno seguiría teniendo a su derecha y a su izquierda a al misma persona.
Cuando las sillas están en fila, esto no pasa, ya que si se mueven todos de silla, por ejemplo un lugar hacia atrás, hay personas que ya no tienen delante o detrás a la misma persona (como es el caso del primero, el penúltimo y el último)
Por tanto, al ser una permutación circular, la fórmula es:
Y aplicando la fórmula a nuestro ejemplo nos queda:
Por lo que se podrían sentar de 24 formas distintas.
Permutaciones con repetición
Las permutaciones con repetición de n elementos son los distintos grupos que pueden formarse con esos n elementos teniendo en cuenta que un elemento se repite «a» veces, otro elemento «b» veces, y así sucesivamente.
En las permutaciones con repetición:
- SÍ intervienen todos los elementos
- SÍ IMPORTA el orden de los elementos
- SÍ se pueden repetir los elementos
Entre los elementos que se repiten, el orden es indiferente, por lo que el número de permutaciones con repetición es menor que las permutaciones ordinarias con los mismos elementos.
La fórmula para calcular las permutaciones con repetición es:
Es decir, se divide el factorial de los elementos totales, entre los factoriales de las veces que se repite cada elemento.
Por ejemplo:
¿De cuántas formas distintas se pueden aparcar 5 coches en línea atendiendo a su color, teniendo en cuenta de que hay 3 coches rojos y 2 azules?
Tenemos 5 coches en total, de los cuales el rojo se repite 3 veces y el azul 2 veces, por tanto, al aplicar la fórmula queda:
Operamos:
Se puede aparcar de 10 formas distintas
Se trata de permutaciones con repetición, porque intervienen todos los elementos, importa el orden y los elementos pueden repetirse.
Esquema para identificar las permutaciones
Como norma general, para saber si se trata de variaciones, permutaciones o combinaciones, te debes hacer las siguientes preguntas:
- ¿Importa el orden?
- ¿Intervienen todos los elementos?
- ¿Se repiten todos los elementos?
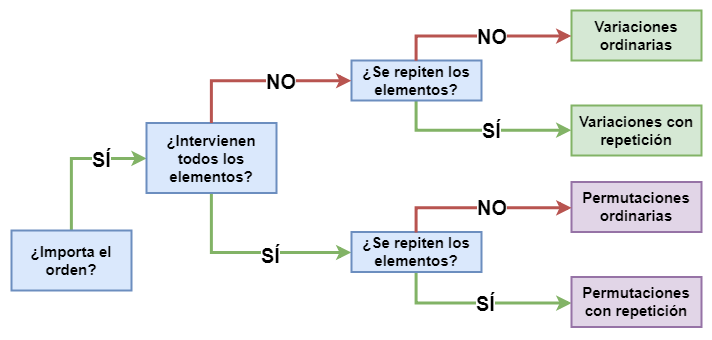
En función de la respuesta estaremos en un caso u en otro. Te dejo aquí el esquema para llegar a las permutaciones, que completa un poco más al que ya teníamos en la lección anterior:
Ejercicios resueltos sobre permutaciones y permutaciones con repetición
Vamos a resolver ahora algunos ejercicios sobre pemutaciones y permutaciones con repetición para que los conceptos te quedan más claros.
Ejercicio 1
¿De cuántas formas se pueden aparcar 8 coches en línea atendiendo a su matrícula?
Tenemos 8 coches que se pueden aparcar en 8 posiciones diferentes. En este caso, importa el orden, se utilizarán todos los elementos y no se pueden repetir, por lo que se trata de permutaciones de 8 elementos.
Aplicamos la fórmula y queda:
Se podrán aparcar de 40320 formas
Ejercicio 2
Con las cifras impares 1, 3, 5, 7 y 9:
a) ¿Cuántos números distintos de cinco cifras se pueden formar?
Utilizamos todos las cifras, importa el orden, ya que si cambiamos la posición de alguna cifra, tenemos un número distinto y las cifras no se pueden repetir. Por tanto es una permutación de 5 elementos, que al aplicar su fórmula y operar tenemos:
Se pueden formar 120 números distintos.
b) ¿Cuántos de los números de cinco cifras son menores que 70000?
Los números que son menores que 70000 empiezan por 1, 3 o 5.
Entonces, por ejemplo, si dejamos el 1 fijo al principio, las combinaciones con las otras 4 cifras formarían todos los números de 5 cifras que empiezan por 1. Entonces, las combinaciones de las otras 4 cifras serían permutaciones de 4 elementos:
Si hacemos lo mismo con el 3 y con el 5, tendríamos otros 24 números que empieza con cada uno, por tanto, tendríamos 24 números que empiezan por 1, 24 números que empiezan por 3 y 24 números que empiezan por 5. 72 números en total menores que 70000:
Ejercicio 3
¿Cuántos números de 6 cifras se pueden formas con los dígitos 1, 1, 2, 2, 3, 3?
Tenemos 6 cifras donde el 1 se repite 2 veces, el 2 se repite 2 veces y el 3 se repite 3 veces. Se toman todas las cifras e importa el orden, por lo que sería una permutación con repetición:
Que operando nos da:
Se pueden formar 90 números de 6 cifras.
¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: