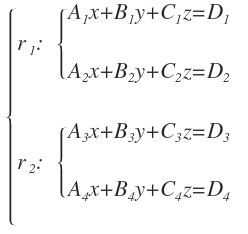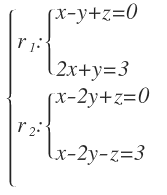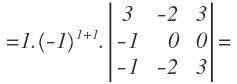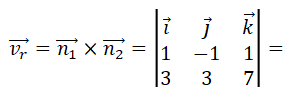Posición relativa de dos rectas en el espacio. Ejercicios resueltos

A continuación te voy a explicar cómo determinar la posición relativa de dos rectas en el espacio. Veremos si las rectas son paralelas, se cortan en un punto, si son coincidentes o si se están cruzando pero sin llegar a tocarse. Con ejercicios resueltos paso a paso.

Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

QUIERO APRENDER MATEMÁTICAS

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Cómo determinar la posición relativa de dos rectas en el espacio

Para determinar la posición relativa de dos rectas en el espacio, hay que resolver el sistema forma por las ecuaciones implícitas de cada recta, que tendría la siguiente forma:

Tendríamos un sistema formado por 4 ecuaciones y tres incógnitas, cuya matriz de los coeficientes es:

Y la matriz ampliada es:

Según los valores de los rangos de A y A* podremos saber la posición relativa de las dos rectas. Los casos que se pueden dar son los siguientes:

Las rectas son coincidentes

Si el rango de A es igual al rango de A* y ambos son iguales a 2, el sistema de ecuaciones es compatible indeterminado, lo que significa que el sistema tiene infinitas soluciones y por tanto, en este caso, las rectas coinciden en infinitos puntos, o lo que es lo mismo, se trata de la misma recta ya que una recta está sobre la otra.

Las rectas son paralelas

Si el rango de A es igual a 2 y el rango de A* es igual a 3, el sistema es incompatible, lo que quiere decir que el sistema no tiene solución y por tanto las rectas no tienen ningún punto en común. En este caso las rectas son paralelas:

Las rectas son secantes

Si el rango de A es igual al rango de A* y ambos son iguales a 3, el sistema es compatible determinado, por lo que tiene una única solución. En este caso las dos rectas son secantes, es decir, se cortan en un punto:

El punto de corte de las rectas es la solución del sistema formado por 3 de las ecuaciones de las rectas, las cuales forman el sistema compatible determinado.

Las rectas se cruzan en el espacio

Si el rango de A es igual a 3 y el rango de A* es igual a 4, el sistema es incompatible. El sistema no tiene solución y por tanto las rectas no tienen ningún punto en común. En este caso las rectas se cruzan en el espacio:

No hay que confundir dos rectas que se cruzan con dos rectas que se cortan. Dos rectas que se cortan, tienen un punto en común. Por otro lado, dos rectas que se cruzan, no tienen ningún punto en común.

Simplemente, una recta pasa por delante de la otra y vistas desde cierta perspectiva parece que se están cortando, pero si cambiamos la perspectiva, veremos como no se cortan en el mismo plano, sino que las rectas están en planos distintos y no llegarán nunca a tocarse.

Ejercicios resueltos sobre la posición relativa de dos rectas

Vamos a resolver paso a paso un ejercicio sobre la posición relativa de dos rectas.

Ejercicio 1

Estudia la posición relativa de las siguientes rectas:

Ya tenemos las ecuaciones de las rectas en su forma implícita, luego directamente podemos pasar a calcular el rango de la matriz de los coeficientes y de la matriz ampliada del sistema.

La matriz de los coeficientes es:

La mayor submatriz cuadrada contenida en la matriz de los coeficientes es de orden 3. Elegimos la formada por las tres primeras columnas y las tres primeras filas, cuyo determinante es:

El determinante de esta submatriz de orden 3 es distinto de cero, luego su rango es igual a 3:

Calculamos ahora el rango de la matriz ampliada, que es la siguiente:

Tenemos un determinante de orden 4, del que debemos calcular su valor (puedes consultar la lección donde explico cómo calcular determinantes de orden 4 para entender mejor los pasos):

Para simplificar los cálculos, voy a realizar operaciones internas en el determinante, para que en la primera columna se quede un 1 en el primer elemento y el resto sean ceros.

Para ello, a la fila 2 le resto 2 veces la fila 1:

A la fila 3 le resto la fila 1:

Y a la fila 4 le resto la fila 1:

El determinante queda de la siguiente manera:

Elijo la primera columna para multiplicar el primer elemento por su adjunto y queda:

Ahora resuelvo el determinante de orden 3 y multiplico por el resto de factores el resultado:

El determinante de la matriz ampliada es igual a cero, lo que significa que el rango va ser menor que 4:

Todo esto lo tienes explicado con detalle en el Curso de Determinantes.

Ahora tenemos que comprobar si el rango de A* es igual a 3, encontrando una submatriz de orden 3 cuyo determinante sea distinto de cero.

Sabemos que el determinante de la submatriz de orden 3 formada por las tres primeras columnas y las tres primeras filas es distinto de cero, ya que es el que utilizamos para calcular el rango de A y esta submatriz también está contenida en A*:

Por tanto, al ser este determinante de orden 3 distinto de cero, el rango de A* también es igual a 3:

Como el rango de A y el rango de A* son iguales a 3, las rectas se cortan en un punto:

Cálculo del punto de corte de dos rectas en el espacio

Esto no lo pide el ejercicio, pero vamos calcular el punto de corte de las rectas. Para ello, resolvemos el sistema formado por las tres primeras ecuaciones, que son las que forman la submatriz de orden 3, cuyo determinante es distinto de cero:

Lo resolvemos aplicando la regla de Cramer.

Calculamos el determinante de la matriz de los coeficientes, que es el siguiente:

La incógnita “x” será igual al determinante asociado a “x” entre el determinante de la matriz de los coeficientes:

La incógnita “y” será igual al determinante asociado a “y” entre el determinante de la matriz de los coeficientes:

La incógnita “z” será igual al determinante asociado a “z” entre el determinante de la matriz de los coeficientes:

Por tanto, el punto P donde se cortan las dos rectas tiene las siguientes coordenadas:

Ejercicio 2

Demuestra que las siguientes rectas representan la misma recta:

Siguiendo el método explicado en la lección, habría que pasarla recta s a sus ecuaciones implícitas y obtener el rango de la matriz de los coeficientes y de la matriz ampliada, que en el caso de ser la misma recta, ambos serían iguales a 2, para que el sistema fuera compatible indeterminado, lo que quiere decir que tendría infinitas soluciones, así que las rectas son coincidentes y por tanto se trata de la misma recta:

Sin embargo, lo resolveremos demostrando que ambas rectas tienen el mismo vector de dirección y que pasan por el mismo punto, para que te des cuenta, de que los ejercicios se pueden resolver utilizando procedimientos distintos.

Vamos a obtener el vector de dirección de la recta r:

Los vectores normales de los planos que forman la recta son:

Calculamos el vector director de la recta r realizando el producto vectorial de sus vectores normales:

Desarrollamos el determinante y nos queda:

Así que, el vector director de la recta r es:

La recta s está expresada en su ecuación continua:

Por lo que podemos obtener directamente un punto perteneciente a la recta y su vector de dirección:

A simple vista, los vectores de dirección de ambas rectas no son iguales, pero si el vector de dirección de la recta r lo simplifico dividiendo sus componentes entre -2, nos queda que es igual al vector director de la recta s:

Demostrar que ambos vectores directores son iguales no es suficiente para comprobar que la recta sea la misma, ya que con esto, lo único que demostramos es que son paralelas.

Para que sean coincidentes, deben pasar por el mismo punto.

Tomamos el punto perteneciente a la recta s:

Y comprobamos si también pertenece a la recta r, sustituyendo x, y y z por las coordenadas del punto y comprobando si se cumple la igualdad:

Operamos y vemos que la igualdad se cumple:

Por tanto, las rectas r y s son coincidentes, ya que sus vectores de dirección son iguales y ambas pasas por el mismo punto.

¿Necesitas ayuda en matemáticas? ¿Quieres que te explique cualquier duda que te surja?

Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.

He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.

Con mi método:

• Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
• Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión

Suena bien ¿no?

¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?

Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más:

ENSÉÑAME MATEMÁTICAS