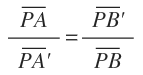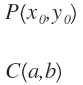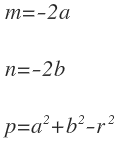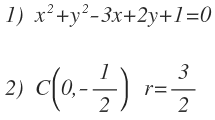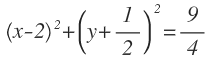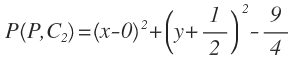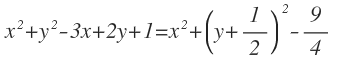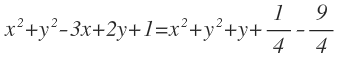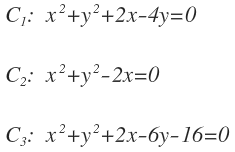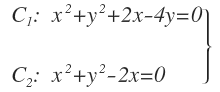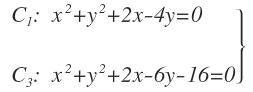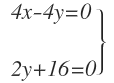A continuación te voy a explicar qué es y cómo se calcula la potencia de un punto respecto de una circunferencia. Veremos también qué utilidad tiene. Además, te explicaré también los conceptos de centro radical y de eje radical. Con ejercicios resueltos paso a paso.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
Qué es la potencia de un punto respecto de una circunferencia
La potencia de un punto respecto de una circunferencia es el valor obtenido después de multiplicar las longitudes de los segmentos de una recta que corta a la circunferencia y pasa por dicho punto.
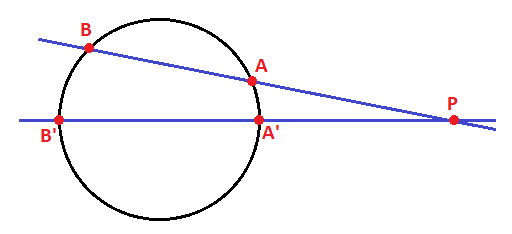
Por tanto, si tenemos una recta que pasa por el punto P y corta a la circunferencia en los puntos A y B:
La potencia del punto P respecto de al circunferencia es igual a la multiplicación de la longitud del segmento PA por la longitud del segmento PB:
Este valor es constante y no depende de la inclinación de la recta, ni de los puntos de corte con la circunferencia. La potencia de un punto respecto de una circunferencia depende de la posición del punto.
Si trazamos otra recta que pase por el punto P y corte a la circunferencia en los puntos A’ y B’:
En este caso, la potencia del punto P respecto de la circunferencia es igual que para la recta que pasa por el punto P y corta en los puntos A y B:
Vamos a demostrar por qué ocurre esto.
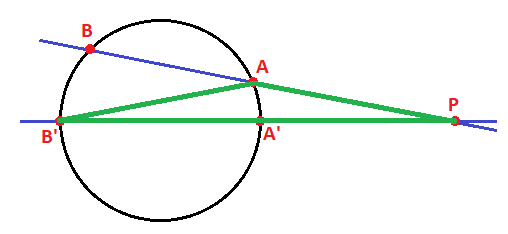
Uniendo los puntos P, A y B’ se forma un triángulo isósceles:
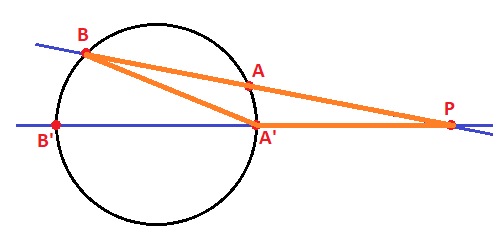
Y si unimos los puntos P, A’ y B formamos otro triángulo isósceles:
Los triángulos PAB’ y PA’B son semejantes al tener dos ángulos iguales, luego se puede establecer una relación entre sus lados homólogos:
Y pasando los denominadores multiplicando al miembro contrario obtenemos que la igualdad que estábamos buscando, es decir, que la potencia del punto P respecto de la circunferencia es constante y no depende de los puntos donde la recta corte a la circunferencia:
Cálculo de la potencia de un punto respecto de una circunferencia
Vamos a ver cómo calcular la potencia de un punto respecto de una circunferencia, conociendo las coordenadas del punto P y la ecuación de la circunferencia, o bien, el centro y el radio de la circunferencia.
Como vimos en el apartado anterior, la potencia de un punto respecto de una circunferencia es el igual a la multiplicación de la longitud de los segmentos en los que la circunferencia corta a la recta:
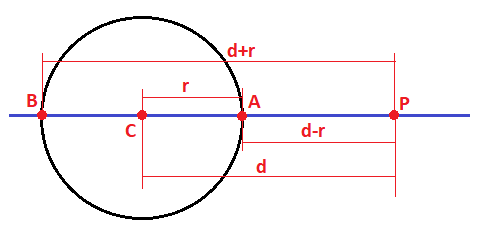
Llamaremos «d» a la distancia entre el punto P y el centro de la circunferencia, de radio r, que coincide con la distancia entre el punto C y A y la distancia entre el punto C y B:
La distancia entre el punto P y A será igual a d-r=
La distancia entre el punto P y B será igual a d+r=
Sustituyendo PA y PB por las expresiones anteriores, nos queda una suma por diferencia, que es igual a la distancia al cuadrado menos el radio al cuadrado:
Si las coordenadas del punto P son X0 e Y0 y las coordenadas del centro de la circunferencia son a y b:
La distancia del punto P al centro es:
Sustituyendo esta expresión por la distancia en la fórmula de la potencia nos queda:
Fórmula que nos sirve para calcular la potencia de un punto a una circunferencia conocidas las coordenadas del punto y centro y el radio de al circunferencia.
Si en la fórmula anterior desarrollamos los productos notables:
Reordenamos términos de la siguiente manera:
Y realizamos los siguientes cambios:
Nos queda la fórmula de la potencia de un punto respecto de una circunferencia conocidas las coordenadas del punto y la ecuación de la circunferencia:
Fórmula que coincide con los términos del primer miembro de la ecuación de una circunferencia.
Posición relativa de un punto con respecto a una circunferencia
El valor de la potencia determinará la posición del punto P con respecto a la circunferencia.
Si la potencia es mayor que cero, el punto P es exterior a la circunferencia:
Si la potencia es menor que cero, el punto P es interior a la circunferencia:
Si la potencia es igual a cero, el punto P pertenece a la circunferencia:
Ejercicios resueltos de la potencia de un punto respecto a una circunferencia
Vamos a resolver uno ejercicios para aplicar lo aprendido hasta ahora.
Ejercicio 1
Halla la potencia del punto P(5,3) respecto de la siguiente circunferencia:
La fórmula para calcular la potencia de ese punto P con respecto de la circunferencia es la siguiente:
Donde X0 e Y0 corresponden a las coordenadas de un punto.
Sustituimos X0 e Y0 por las coordenadas del punto P y operamos:
La potencia es mayor que cero, lo que significa que el punto es exterior a la circunferencia.
Ejercicio 2
Indica la posición relativa de los puntos A(-1,3) y B (2,3) con respecto de la circunferencia del ejercicio anterior:
La ecuación de la circunferencia del ejercicio anterior es:
Para obtener la potencia de un punto respecto de una circunferencia necesitamos calcular su potencia.
La potencia del punto A con respecto a la circunferencia es:
La potencia es menor que cero, por lo que el punto A es interior a la circunferencia:
Calculamos la potencia del punto B con respecto a la circunferencia:
La potencia es igual a cero, por lo que el punto B pertenece a la circunferencia:
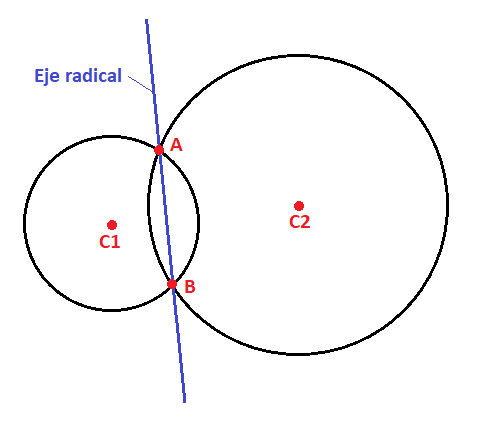
Eje radical de dos circunferencias
El eje radical de dos circunferencias es la recta que contiene los puntos que tienen la misma potencia respecto de las dos circunferencias.
Cómo calcular el eje radical de dos circunferencias
Vamos a resolver un ejercicio para saber cómo calcular el eje radical de dos circunferencias.
Por ejemplo: Hallar el eje radical de las siguientes circunferencias:
En primer lugar obtenemos la ecuación de la segunda circunferencia, ya que nos dan el radio y el centro:
En el eje radical, las potencias de un punto P que pertenezca a la recta respecto de las dos circunferencias tendrá el mismo valor. Por tanto, lo que tenemos que hacer es calcular la potencia de un punto respecto a cada circunferencia y luego igualarlas.
La potencia de un punto P del eje radical con respecto a la primera circunferencia es:
La potencia de un punto P del eje radical con respecto a la segunda circunferencia es:
Igualamos ambas potencias:
Desarrollamos el producto notable:
Los términos elevados al cuadrado se anulan y operamos las fracciones:
Pasamos todos los términos al primer miembro y reordenamos términos:
Nos queda la ecuación de una recta, que corresponde a la ecuación del eje radical.
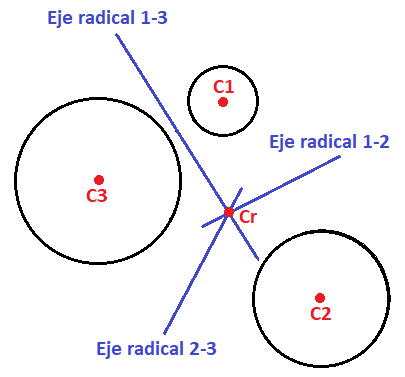
Centro radical de tres circunferencias
El centro radical de tres circunferencias es un punto que tiene la misma potencia respecto de las tres circunferencias. Es el punto de corte de los ejes radicales de las circunferencias obtenidos dos a dos:
Cómo calcular el eje radical de tres circunferencias
Vamos a calcular el eje radical de las siguientes tres circunferencias:
Empezamos igualando las potencias de las dos primeras circunferencias, con el fin de calcular su eje radical:
Después de operar nos queda la ecuación del eje radical de las dos circunferencias:
Necesitamos otro eje radical, ya el punto de corte de los dos ejes radicales determinará el centro radical. Para ello, obtenemos el eje radical de la primera y la tercera circunferencia:
Igualamos ambas potencias:
Operamos y nos queda la ecuación de otro eje radical:
Para obtener el punto de corte de ambos ejes, resolvemos el sistema formado por los ejes:
Cuya solución es:
Por lo que el centro radical es:
¿Necesitas ayuda con las matemáticas? ¿Quieres que te explique cualquier duda que te surja paso a paso?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: