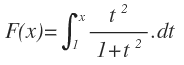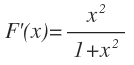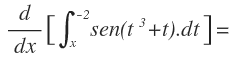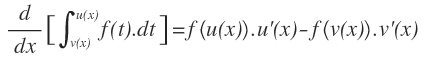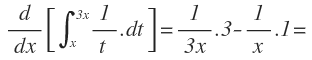¿Quieres aprender a derivar integrales de funciones aplicando el teorema fundamental del cálculo? Te lo explico en esta lección paso a paso, con ejercicios resueltos.
Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.
¡Vamos allá!
El primer teorema fundamental del cálculo nos dice que la integración es la operación inversa a la derivación.
Fórmula del teorema fundamental del cálculo integral
Tenemos una integral de una función que depende de la variable t (con su correspondiente diferencial de t), que va desde una constante «a» hasta la variable «x», a la que llamaremos F(x):
Si derivamos toda esa integral con respecto a x, el resultado es la misma función que dependía de t en la integral, pero ahora dependiendo de x:
Es decir, la derivada de la integral de una función, es esa propia función. Lo que demuestra que derivar es la operación inversa a integrar.
La aplicación de este teorema es muy sencilla, ya que sólo tenemos que sustituir la t por la x en la función que estamos integrando.
Ejercicios resueltos del teorema fundamental del cálculo
Por ejemplo, hallar la derivada de la siguiente integral usando el teorema fundamental:
A esa expresión la llamamos F(x):
Nos están pidiendo calcular la derivada de F(x), es decir F'(x), que es la derivada de la integral con respecto de x:
Por tanto vamos a resolver esta derivada de aquí:
Aplicando la fórmula del teorema fundamental del cálculo:
La función en este caso f(t) es:
Para hallar f(x), solamente tenemos que sustituir la x por la t en la función f(t) que está dentro de la integral. Al sustituir la t por la x nos queda f(x):
Por tanto, la derivada de la integral es:
Que es lo mismo que decir que la derivada de F(x) es igual a f(x):
Debes tener cuidado ya que en la fórmula del teorema fundamental, la integral va desde la constante «a» hasta la variable «x», por tanto, si la integral está escrita al contrario, debes darle la vuelta a la integral y ponerle un signo menos delante para que su resultado no varíe.
Vamos a ver esto con un ejemplo: Hallar la derivada de la siguiente integral usando el teorema fundamental:
Nos piden derivar con respecto a x esta integral:
Vemos que la integral va desde x hasta -2 y para poder aplicar la fórmula del teorema fundamental, debería ir desde -2 hasta x, por tanto, le damos la vuelta a la integral y le colocamos un signo menos delante para no variar su resultado (según las propiedades de las integrales):
Por tanto, la derivada de la integral original, la sustituimos por la derivada a la que le hemos dado la vuelta y lleva un signo menos delante:
Y ese signo menos lo podemos sacar fuera de la integral:
Ahora ya podemos aplicar la fórmula del teorema fundamental, teniendo en cuenta de que tenemos un signo menos delante:
f(t) es:
Sustituimos la x por la t para obtener f(x):
Por lo que la derivada de la integral, teniendo en cuenta el signo menos que lleva delante es:
Como la derivada de la integral original es igual a la derivada de la integral a la que hemos dado la vuelta y con el signo menos delante:
El resultado de la derivada de la integral original es:
Fórmula del teorema fundamental para derivar integrales que van desde una constante hasta una función
Hasta ahora hemos visto como derivar integrales que van desde una constante hasta la variable x, pero ¿cómo se aplica el teorema fundamental del cálculo cuando queremos derivar integrales que van desde una constante hasta una función?
Te voy a explicar cómo aplicar la fórmula del teorema fundamental para derivar integrales que van desde una constante hasta una función, en vez de ir desde una constante hasta la variable x, es decir, te voy a explicar cómo derivar integrales como ésta, a la que llamamos F(x):
aplicando el teorema fundamental.
En este caso, la derivada de F(x) con respecto de x será igual a la función f(u(x)), por la derivada de u(x). El resultado es la misma función que dependía de t, pero ahora dependiendo de u(x) y multiplicada por la derivada de esa función u(x):
Vamos a ver cómo aplicar esta fórmula con un ejemplo: Hallar la derivada de la siguiente integral:
Vamos a calcular la derivada de esta integral con respecto a x utilizando el teorema fundamental:
Idenficamos u(x) que es:
Obtenemos f(u(x)), sustituyendo la t por u(x):
Y calculamos u'(x) derivando u(x):
Por tanto, la derivada de la integral original, aplicando la fórmula del teorema fundamental es igual a:
Fórmula del teorema fundamental para derivar integrales que van desde una función hasta otra función
Finalmente te voy a explicar cómo aplicar la fórmula del teorema fundamental para derivar integrales que van desde una función hasta otra función, como ésta:
Para derivar integrales que van desde una función hasta una función la fórmula del teorema fundamental es la siguiente:
Y para entenderla mejor vamos a aplicarla derivando la siguiente integral:
Queremos derivar esa integral con respecto a x:
Vamos a definir cada uno de los componentes que aparecen en la fórmula. v(x) y u(x) son:
Para obtener f(u(x)) sustituimos la t en f(t) por u(x):
Para obtener f(v(x)) sustitimos la t en f(t) por v(x):
Las derivadas de v(x) y u(x) son:
Lo sustituimos todo en la fórmula quedando:
Y si seguimos operando, el resultado es:
¿Necesitas clases de matemáticas online? ¿Quieres que te explique cualquier duda que te surja?
Puedo enseñarte exactamente lo que necesitas aprender para aprobar las matemáticas.
He diseñado un método práctico y efectivo que te ayudará a entender las matemáticas, paso a paso, explicándote justo lo que necesitas para saber resolver todos tus ejercicios y problemas. Todo con un lenguaje sencillo y ameno que entenderás perfectamente.
Con mi método:
- Sabrás los pasos exactos que tienes que dar para resolver tus ejercicios y problemas
- Conseguirás resultados en muy poco tiempo, sin dedicar más horas a intentar entenderlo por tu cuenta sin llegar a ninguna conclusión
Suena bien ¿no?
¿Por qué tardar 2 horas buscando por Internet si puedes aprenderlo en menos de 20 minutos?
Sé lo que te impide entender las matemáticas y sé lo que necesitas para entenderlas. ¿Quieres informarte de como puedes aprender matemáticas conmigo? Pulsa el botón para saber más: